表面積｜教養数学

学習目標

網を理解する
網を使ってプリズムを表現することができる。
プリズムの表面積を求める。
円柱の表面積を求める。
球の表面積を求める。

ネット

固体を表現する最後の方法としてネットを使用することが挙げられます。網を切り取れば、それを折って図形の模型にすることができます。ネットはまた、単一の固体を分析するために使用することができます。

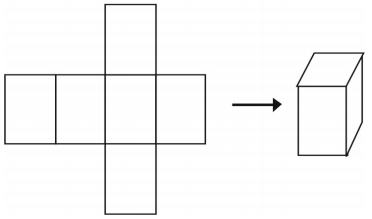
1つの図形に対して網を作る方法は1つではありません。

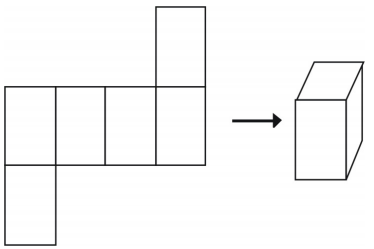
ただし、すべての配置が立方体を作るわけではありません。

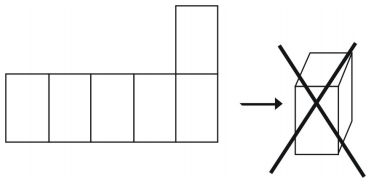
例1

その網でどんな図形ができるでしょうか。

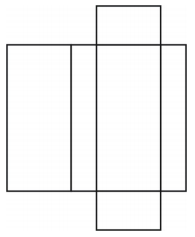
網は下図のような箱型の直方体を作ります。

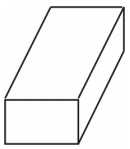
例2

図のような網にはどんなものが描けるでしょうか。

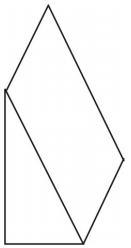
角柱の網が描かれています。他のネットも可能です。

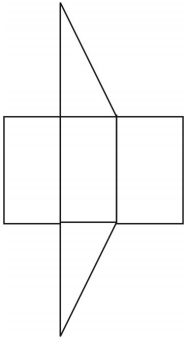
Review Exercises

以下のそれぞれについて網を描け。

答え

プリズム

プリズムとは平行に一致した一対の端（底）を持つ立体図形を指します。角柱の辺は平行四辺形である。

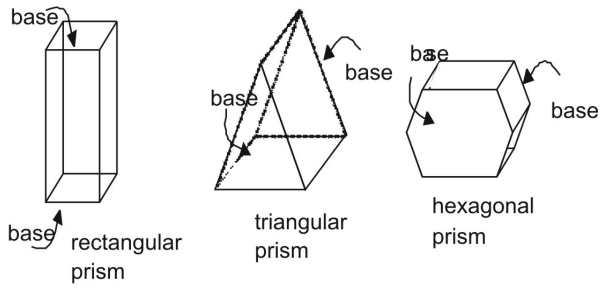
網を使ったプリズムの表面積

上のプリズムは右プリズムである。直角プリズムでは、横の辺がプリズムの底面に対して垂直である。

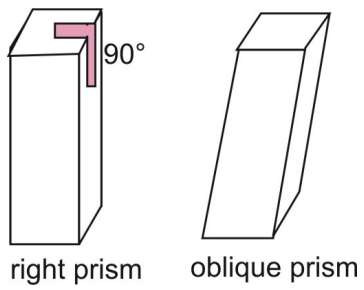
面積に適用される二つの定石は面積合同定石と面積加算定石です。

面積合同定立：2つの多角形（または平面図形）が合同であれば、それらの面積は合同である。

網と面積加算則を使って、直方体の表面積を求めることができます。

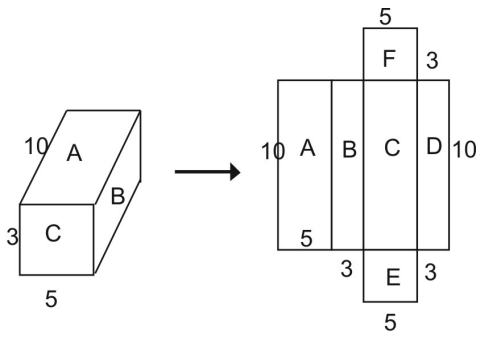
網から、プリズム全体の表面積は網を構成する図形の和に等しいことがわかります。

全体の表面積＝面積A＋面積B＋面積C＋面積D＋面積E＋面積F

直方体の面積の公式を使って、直方体の面積Aを求めると

A = l – w
A = 10 – 5 = 50平方単位

同様に、他の長方形の面積を上の式に挿入し直します。

総面積＝面積A＋面積B＋面積C＋面積D＋面積E＋面積F
総面積＝（10 – 5）＋（10 – 3）＋（10 – 5）＋（10 – 3）＋（5 – 3）＋（5 – ）。 3）＜3543＞総面積＝50＋30＋50＋30＋15＋15＜3543＞総面積＝190平方単位＜7676＞＜1271＞＜603＞例3＜8639＞＜4518＞ネットを使ってプリズムの表面積を求めます。

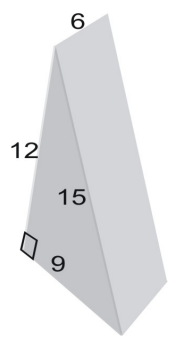
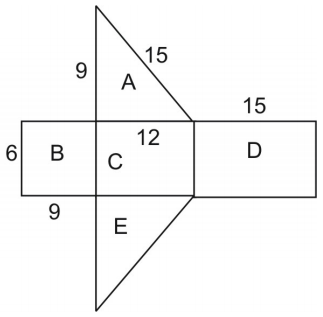
網の面積は図形の表面積と同じです。三角形の面積を求めるには次の式を使います：

displaystyle{A}=hfrac{1}{2}hb** ここでhは三角形の高さ、bは底辺です。

なお、三角形AとEは合同なので、面積に2をかければよい。

displaystyle text{area}=C+text{area }A+text{area }B+text{area }C+text{area }D+text{area }E
displaystyle text{ }=2(\text{area }A)+thext{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\

Thus, 表面積は324平方単位です。

Review Exercise

次のそれぞれについて、網の目法を用いて表面のaを求め、周囲を求める

ある角柱の底は脚が3と4、高さは20とする直角三角形である。
直六角柱は高さが24インチで、底面は一辺が8インチの正六角形である。
問題4のプリズムの体積は？

以下の問題で、納屋の形は五角柱で、寸法はフィートで示されています：

塗装される納屋の表面には何平方フィート（屋根は含まない）ありますか？
1ガロンのペンキが250平方フィートをカバーする場合、納屋を塗装するには何ガロンのペンキが必要ですか？
ダンボール箱は、端が17インチの完全な立方体です。
プールは幅16フィート、長さ32フィートで、深さは一様に4フィートである。
シリアルの箱は長さ25センチ、幅9センチ、高さ30センチである。シリアルは何個入りますか？

答え

網と周囲：

40.5 in2
838 cm2
252平方単位
1484.5 in1
252 平方単位
252 平方単位
252 平方単位
252 平方単位。6平方単位
3990.7 立方インチ

The barn:

2450 square feet
10 gallons of paint
2.85 cubic feet（ここは注意です。問題の単位はインチで与えられていますが、問題はフィートを求めています。）
2048 立方フィート
6750 cm3

Cylinders

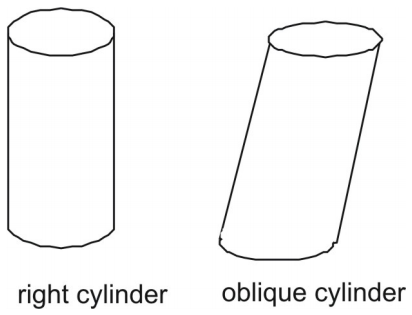
A cylinder is a three-dimensional figure with a pair of parallel and congruent circular ends, or base.

角柱と同様、円柱にも直角と斜めの2種類がある。直円柱の側面は円形の底面に対して垂直である。

網を使った円柱の表面積

円柱を網に分解することができる。

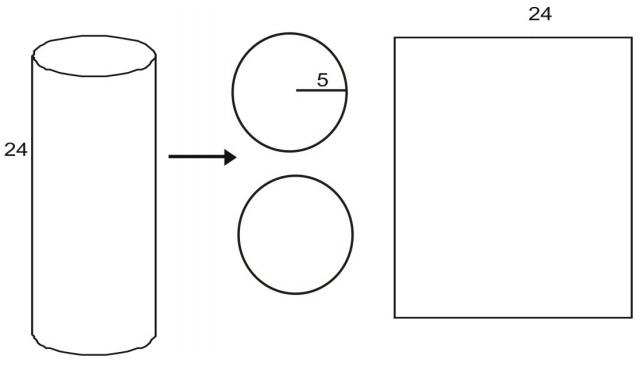
各底面の面積は円の面積で与えられる：

A=Copy{r}^2
A=Copy(5)^2
A=25pi
Aapprox(25)(3.14)=78.5 Encite

直方体の側面領域Lは幅と高さの積によって与えられる。高さは24で与えられる。幅は円形の底面の円周に等しいことがわかる。

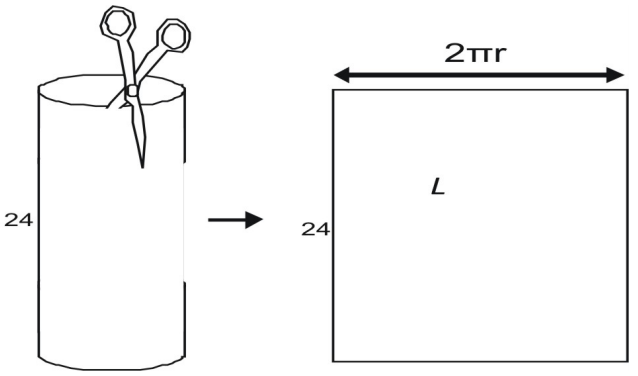
幅を求めるには、缶のような円筒をはさみで切り離すことを想像してください。横の部分を切ってみると、缶の上部の円周と同じであることがわかります。円の円周はC=2πrで、横の面積Lは

L=2{pi}rh
L=2{pi}(5)(24)\
L=240Lapprox(240)(3.14)=753.6 Θ

ここで、A=(2つの底面の面積)+(横面の面積)で円柱全体の面積を求めることができる。

A=2(75.36)+753.6A=904.32 総面積を求める式は、どの直円筒でも使えることがわかります。半径と高さhの直円柱の表面積はA = 2B + Lで与えられ、Bは円柱の各底面の面積、Lは円柱の横方向の面積です。

例4

網を使って、円柱の表面積を求めます。

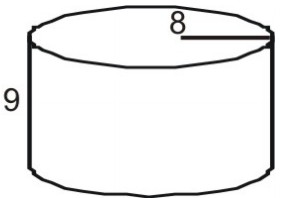
まず図の網を描いてラベルを貼る。

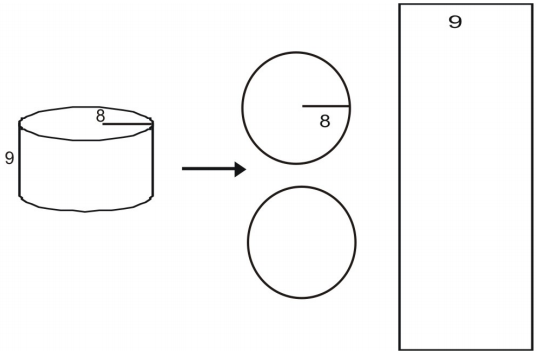
各底面の面積を計算する。

A=Pi{r}^2 ◇
A=pi(8)^2 ◇
A=64 ◇
Aapprox(64)(3.14)=200.96\\

Calculate L.

L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16 ⑯

Find area of the entire cylinder.

A=2(200.96)+452.16 ⑯A=854.3 ⑯A=854.08

This is approximately 854.08 square units

Surface Area of a Cylinder Using a Formula

網を使って円柱の総面積を求める方法を見てきましたね。この仮定を分解して、すべての直円筒の一般式を作ることができます。

A = 2B + L

任意の円柱の底面Bは：B = πr2

任意の円柱の側面面積Lは：。

L=Text{width of lateral area}cdottext{height of cylinder}
L=Text{circumference of base}cdottext{height of cylinder}
L=2π{r}cdot{h}cp

二つの方程式を合わせると次のようになる。

式からaを因数分解すると：

The Surface Area of a Right Cylinder.となる。半径r、高さhの直円筒は次のように表される：

A = 2πr2 + 2πrh

または：

A = 2πr(r + h)

この式を使って、任意の直円筒の面積を求めることができます。

例題5

式を使って円柱の表面積を求めます。

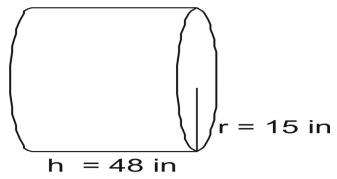
式を書き、値を代入して解きましょう。

A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6text{ square inches}}

Example 6

Find the surface area of the cylinder.

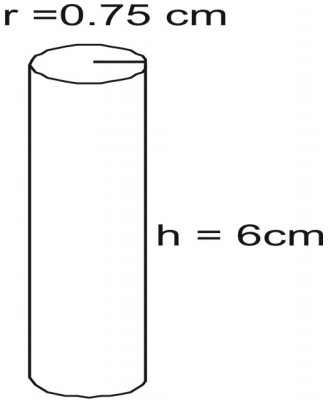
式を書き、値を代入して解く。

A=2π{r}(r+h)\
A=2(3.14)(0.75)\
A=31.7925text{ square inches}

Example 7

半径4cm、表面積226.08平方cmの円柱の高さを求めよ。

与えられた情報で式を書き、hを解きなさい。

A=2π{r}(r+h)\
226.08=2(3.14)(4)\
226.08=25.12h
5=h

Spheres

球は球形の立体図形であり、球は、球の形状をしていて、球が球体である。

球は3つの方法で特徴付けることができる。

球は単一の中心点Oから一定距離rにあるすべての点の集合である。
球面とは、円をその直径のどれかで回転させたときの表面である。

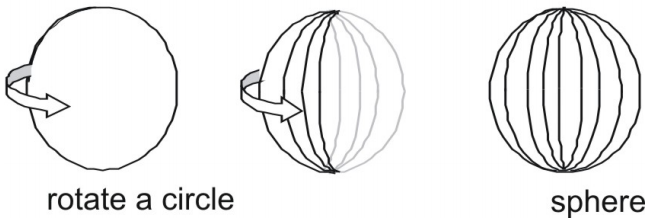
球面の表面積

球面や円柱を測定することにより、球面の面積の公式を推測することができる。ここでは半径が3の球と、半径と高さがともに3の直円柱を示し、面積をπで表します。

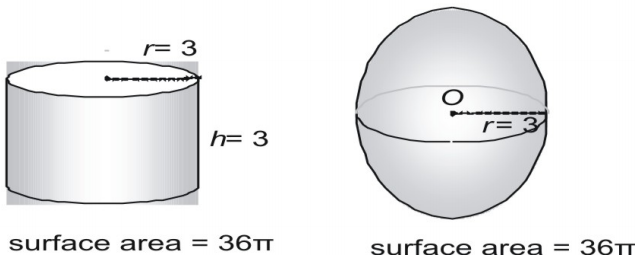
今度はもっと大きなペアで、表面積を10進数で表してみましょう。

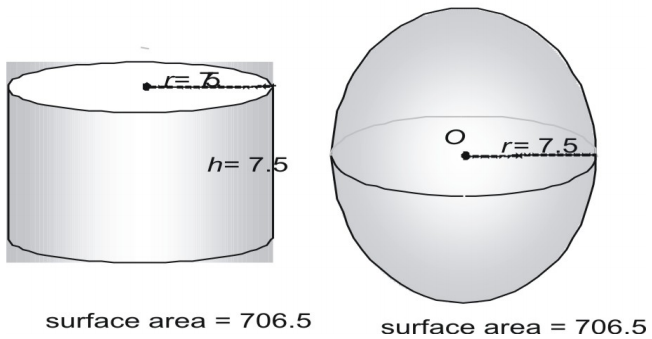
3番目のペアを見てみましょう。

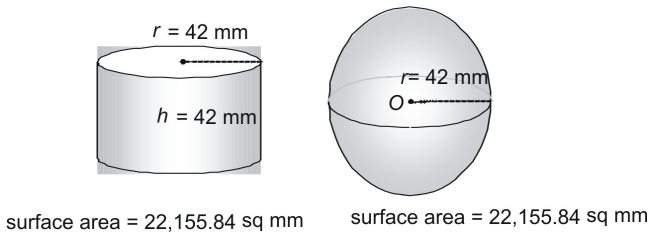
球と球の半径と高さが同じ円柱が全く同じ表面積になるのは偶然でしょうか？そんなことはありません。実は、古代ギリシャ人は、次の式を使って、どんな球体（またはその中のどんな円柱）の表面積も求めることができることを示す方法を用いていた。

球体の表面積は、次の式で与えられる。 A = 4πr2

Example 8

Find the surface area of a sphere with a radius of 14 feet.

Use the formula.A=4pi{r}^2
A=4pi(14)^2 ◇
A=4π(196)◇
A=784 ◇
2461.A

Copy(196)76text{ square feet using }3.14text{ for }pi

Example 9

以下の図形の表面積をπで求めよ。

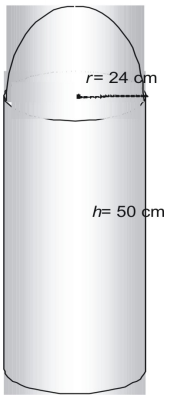
この図形は半球または半球が1つと、頂点のない円柱が1つで構成されている。

A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half sphere})=2pi(576)\
A(\text{half sphere})=1152pitext{ square cm}

ここで、円柱の上部を除いた面積を求めなさい。

A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\

Thus, 総表面積は1152pi+2976pi=4128pi