Sun, 18 Jun 2006
1+1=2
ホワイトヘッドとラッセルのプリンキピア・マテマは1+1=2を1000ページかけて証明することで有名である。 もちろん、それ以外のこともたくさん証明されている。
Principia Mathematicaは、数学的な観点だけでなく、歴史的な観点からも調べてみる価値のある、奇妙な本です。 この本が書かれたのは1910年頃で、当時はまだ数理論理学はペアーノやフレーゲによる変換が行われたばかりで、黎明期であった。 その後、数学的な表記法が大幅に進化したため、表記法はやや曖昧である。 また，現在では当たり前のように使われている簡単な技法も多くありません．出来の悪いコンピュータプログラムのように，『プリンキピア・マテマティカ』の大部分は繰り返し書かれたコードで，本質的に同じことを述べている別々のセクションです．
例えば、セクション＊22「クラスの計算」では、まず部分集合関係（＊22.01）を定義し、集合和と集合積の操作（＊22.02と03）、集合の補数（＊22.04）、二つの集合の差（＊22.05）などを定義しています。 そして、集合の和と集合の交の可換性と結合性（∗22.51, .52, .57, .7）、! \alpha\capalpha = \alpha!等の諸性質を証明する。 (∗22.5)などの様々な性質を説明し、∗22.92: !!\alphasubset01）、関係の和と差の演算（∗23.02, 03）、関係の補数（∗23.04）、2つの関係の差（∗23.05）などが定義されています。 さらに、関係の結合と交差の可換性と結合性（∗23.51, .52, .57, .7）、!alpha= \alpha! (∗22.5) などの諸性質、∗23.92のような定理に至るまで、: !!!㊞㊞㊞㊞㊞㊞㊗(㊞㊞️㊗)！＜5283＞24 項ではセットの存在、空集合 !!!、普遍集合 !!!｛rm V｝!! について述べている。そして、＊24節は＊25節と重複して、関係の存在、空関係 !!!、普遍関係 !!!、それらの性質などに関する一連の定理を述べています。 現在ではどうだろうか。 SとTの間の関係はS×Tの部分集合として定義され、したがって集合である。 関係は集合であるから、単離、交叉、差などの演算は集合の場合と全く同じである。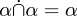 
のような関係の結合と交差に関する定理は、集合に対してすでに証明されており、関係は集合であるから、そのまま消えてしまう。 空関係(nullrelation)は空集合(null set)である。
2006年には、関係と集合の統合のために、膨大な量の他の機械がなくなっている。 Principia Mathematicaは、関係を、その第1要素が特定の集合Sのメンバーであるか、その第2要素がSのメンバーであるか、その要素の両方がSのメンバーである対に制限した結果について、特別な表記と特別な定義を必要としています。
Whitehead と Russell は 1910 年当時、順序対という重要な機械が欠けていたため、これを行うことができなかった。 1910年当時、誰も論理と集合だけで順序対を作る方法を知りませんでした。 2006年（あるいは1956年）には、順序対<a, b>を集合{{a}, {a, b}}として定義することになります。 そして、集合の性質を利用して、a=cかつb=dのときのみ、<a, b>=<c, d>となることを定理として示すことになるでしょう。 そして、p=<a,b> ∧a∈A∧b∈B となるすべてのpの集合をA×Bと定義し、集合A、Bの関係をA×Bの部分集合と定義することになります。 そうすると、＊23と＊25と＊35と＊36の全部がタダで手に入るし、他のものもたくさん手に入る。 これは通常 Norbert Wiener によるとされていますが、Wiener のアイデアは似ているものの、実際にはもっと複雑なものでした)
Principia Mathematica には暗黙の了解を除いて順序付きペアはありません。 集合もほとんどない。 ホワイトヘッドとラッセルはすべてを論理学にもとめようとしています。 ホワイトヘッドとラッセルにとって、基本的な概念は「命題関数」であり、それは真理値を出力とする関数φである。 このような関数にはそれぞれ対応する集合があり、彼らはこれをφ(x)が真となるすべてのxの集合である! \hat xphi(x)!!で表す。 ホワイトヘッドとラッセルにとって、集合が1変数の命題関数によって暗示されるのと同様に、2変数の命題関数によって暗示されるのがアレレーションである。 2006年、我々は「2変数の関数」を捨て、（単一の）引数が順序付きペアの関数についてだけ話す。
ラッセルはシェファーストローク（他のすべての論理演算子を構築できる単一の論理演算子）の発見は途方もない進歩であり、すべてを変えるだろうと述べたとされている。 というのも、シェファー・ストロークの発見はとてもシンプルで、重要なことは何も変わっていないように思えるからだ。 第1章の最初に∼pとp∨qはそれぞれp|pとp|p.|.q|qの省略形であることを書き加えて、5つの基本公理を証明し、他のすべてはそのままにしておけばよいのである。 しかし、ラッセルは、順序対が集合として解釈できるという発見についても同じことを言ったかもしれない。それは、本当に『プリンキピア・マテマティカ』をまったく別の作品に変えてしまったかもしれない単純な発見である。 これは『プリンキピア・マテマティカ』の後半、＊102節で行われる。 私の要約版では、＊56までしか書かれていませんが、重要な前駆定理である＊54.43までは十分な距離があり、以下にスキャンします。
これが証明される定理で、以下はその証明です。
さて、1910年から多少変わっている表記法を説明しましょう。 まず、Principia Mathematicaでは、Peanoの「ドット」表記を用いて優先順位を曖昧にしますが、現在は代わりに括弧を用います。 ドット記法には慣れが必要ですが、括弧に比べていくつかの明確な利点があります。 つまり、(1+2)×(3+4)&回(5+6)は、1+2.×.3+4.×.5+6と表記されます。 同様に、(5+6) の部分式は、左の点と右の式の終わりで区切られています。
もし括弧を入れ子にする必要があったらどうしますか。 その場合は、さらにドットを使用します。 ダブルドット(:)はシングルドットに似ていますが、より強力です。 たとえば、((1+2)×3)+4 と書くと、1+2 . × と書くと、ダブルドットは1+2 .
時には、より多くの優先順位が必要で、3連符（.:と:.）や4連符（::）を使用することがあります。 この式は、ご覧のように2重と3重のドットがあります。 ドットを標準的な括弧書きに変換すると、$$ast54.43となる。 \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha ⑅cap⑅ = \Lambda) \equiv (\alpha⑅cup⑅) ))$$. これは、ドットを使ったバージョンよりも見た目が雑で、複雑な数式ではどの括弧とどの括弧が一致するのかわからなくなることがあります。 ドットを使えば簡単です。 2001>
「！！！！！！！！！！！！！！！」という記号は変わっていません。 Λは空集合で、現在では∅と書きます。 ∩∪と∈は現代的な意味で、∩と∈は集合の交差と和集合の演算子で、x∈yはxが集合yの要素であることを意味する＜2001＞＜5283＞残りの点は意味である。 1はちょうど1つの要素を持つすべての集合の集合を表します。 つまり、{ c : c = {a } となるようなaが存在する}という集合である。 }. 1に関する定理としては、例えば、
- that Λ∉1 (＊52.21),
- that if α∈1 then there is some x such that α ={x}. (＊52.1)、＜4885＞＜3307＞その{x}∈1 (＊52.22)です。
2も同様に、ちょうど2つの要素を持つすべての集合の集合である。 2に関する重要な定理に∗54.3があり、$$ast54.3が書かれています。 \vdash 2 = \hatalpha{ (\exists x) \> .\>xinalpha} . \> \alpha – \iota`xin 1 \}.$$Principia Mathematicaの表記では、xを含み他にない集合である{x}はι’xと書かれるので、この定理は、αが何らかの要素xを持ち、αから取り除くと1要素の集合が残るようなすべてのαの集合と2は同一であることを述べています。
ここで再び定理＊54.43を紹介します。
これは、集合αとβがそれぞれちょうど1つの要素を持つとき、それらの和がちょうど2つの要素を持つ場合にのみ、それらが不連結（つまり共通の要素を持たない）であると主張するものである。
証明は、上記のスキャンで “Dem.” (demonstrationの略) の後に表示され、次のようになります。
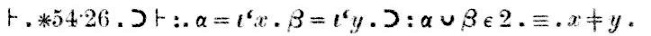
“Theorem∗54.26implies that if α = {x} and β = {y}, thenα∪β has two elements if and only if x isdifferent from y”.” は、α={x} と β={y} のとき、α∪βはxがyと異なる場合にのみ2つの要素を持つことを意味します。
“定理＊51.231により、この最後のビット（x is different fromy）は{x}と{y}がdisjointである場合に限り真である。”
“＊13.12により、この最後のビット（{x}と{y}は不一致）は、αとβ自体が不一致である場合にのみ真である。” (1)と書かれているこの時点の部分結論は、α＝{x}とβ＝{y}なら、α∪β∈2 if and only if ∩β＝Λ というものです。
証明は続く。 “結論（1）は、定理＊11.11と＊11.35により、αが{x}でβが{y}であるようにxとyが存在するならば、αとβが不一致の場合にのみα∪β∈2 を意味する。”となる。 この結論に(2)のラベルが貼られている。
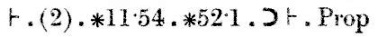
最後に、(2)の結論は、定理＊11.54と＊52.1と共に、我々が証明しようとした定理を意味します。
Principia Mathematica の後の部分は見ていません。私の本は、＊56節で止まっていて、算術的なものはずっと後のものだからです。 しかし、この定理には明らかに1+1=2の意味があり、実際に1+1=2を主張している後の定理（∗110.643）はこの定理に強く依存している。
この後どうなるかは全くわからないのですが、（図書館で完全版を買うにはもう時間がかかりすぎる）一応の予想はつきます。 Principia Mathematica は17という数字を17個の要素を持つ集合の集合として定義するつもりです． ある大きさのすべての集合の集合は「基数」として識別されることになる。
Principia Mathematicaでは、基数pと基数qの和を次のように定義している：pから代表集合aをとる；aはp個の要素をもつ。 qから代表的な集合bを取り、bはq個の要素を持つ。 c =a∪b とする。 cがある基数rのメンバーであり、aとbが不連結であれば、pとqの和はrである。
この定義により、x + 0 = x、x + y = y + x、1 + 1 = 2といった通常の望ましい加算の性質を証明することができる。
特に、1+1=2は定理＊54.43から直接導かれます。1+1を計算するには、1の不連続な代表を2つ見つけ、それらの和を取らなければならないので、これはまさに我々が望むところです。＊54.43は、どの代表を選んでも、その和が2の要素でなければならないと主張しているので、1+1=2となっているのです。
Post scriptum: Peter Norvig は、Principia Mathematica の表記法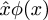 
の circumflex が、Lisp や Python プログラミング言語における匿名関数を表す単語 lambda の究極の源だと言っている。 これらの言語が「ラムダ」を獲得したのは、アロンゾ・チャーチが彼の「λ-calculus」で関数の抽象化を表現するためにギリシャ文字のλを使ったことに由来することはご存じかと思います。 Lispでは、(lambda (u) B)は引数uをとってBの値を返す関数です。λ-calculusでは、λu.Bは引数uをとってBの値を返す関数です。Norvigによると、Churchはもともと関数λu.Bを û.B として記述しようとしましたが、彼のプリンタは周束アクセントに対応できなかったそうです。 大文字のΛΛは論理的で∧に見えすぎて混乱するので、代わりに小文字のλλ.Bを使いました。
Post post scriptum: みんないつも「ラッセルとホワイトヘッド」と言う。 なぜか？ 表紙やタイトルページには「Alfred North Whitehead and Bertrand Russell,F.R.S. 」と書かれているのですが。 いつ、どのようにして、ホワイトヘッドがトップバッターを失ったのでしょうか？
permanent link