yourbasic.org
Amortized analysis is used for algorithms that have expensive operations that happen only rarely.

償却済み複雑性分析は、操作間に持続する状態を持つデータ structuresthat で最もよく使用されています。基本的な考え方は、高価な操作は、最悪のケースが長い間再び起こらないように状態を変更することができ、したがって、そのコストを償却することである。
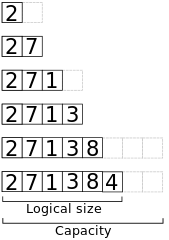
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++以下は、容量 2 の最初は空の配列に要素 2, 7, 1, 3, 8, 4 を追加するときのメモリの様子です。
ワーストケース時間
このアルゴリズムを使って、長さnの配列に要素を追加する場合のワーストケース時間複雑度は、Θ(n)である。次のn回の追加操作はもっと安くなる。新しく割り当てられた配列にはすべての新しい要素を入れるスペースがあるので、それぞれの操作は一定時間で実行される。 注意深く分析すると、これらの操作の合計時間はΘ(n)だけであることがわかる。
- 合計n回の定時間割り当てとインクリメント操作がある。
- サイズ変更は操作1、2、4、…、2kでだけ行われ、合計1 + 2 + 4 + … + 2k = 2-2k – 1の定時間要素コピー操作となる。 2k ≦ nなので、これは最大でも2n – 1である。
したがって、単一の追加操作の償却済み時間複雑度はΘ(1)である。
アルゴリズム分析の詳細

時間複雑度を表示する。 Count your steps

Big O notation