La pressione indica la forza normale per unità di superficie in un dato punto che agisce su un dato piano. Poiché non ci sono tensioni di taglio presenti in un fluido a riposo – la pressione in un fluido è indipendente dalla direzione.
Per i fluidi – liquidi o gas – a riposo il gradiente di pressione in direzione verticale dipende solo dal peso specifico del fluido.
Come la pressione cambia con l’elevazione in un fluido può essere espressa come
Δp = – γ Δh (1)
dove
Δp = variazione di pressione (Pa, psi)
Δh = variazione di altezza (m, in)
γ = peso specifico del fluido (N/m3, lb/ft3)
Il gradiente di pressione in direzione verticale è negativo – la pressione diminuisce verso l’alto.
Peso specifico
Il peso specifico di un fluido può essere espresso come:
γ = ρ g (2)
dove
ρ = densità del fluido (kg/m3, lumache/ft3)
g = accelerazione di gravità (9.81 m/s2, 32.174 ft/s2)
In generale il peso specifico – γ – è costante per i fluidi. Per i gas il peso specifico – γ – varia con l’elevazione (e la compressione).
La pressione esercitata da un fluido statico dipende solo da
- la profondità del fluido
- la densità del fluido
- l’accelerazione di gravità
Pressione statica in un fluido
Per un fluido incomprimibile – come un liquido – la differenza di pressione tra due quote può essere espressa come:
Δp = p2 – p1
= – γ (h2 – h1) (3)
dove
p2 = pressione al livello 2 (Pa, psi)
p1 = pressione al livello 1 (Pa, psi)
h2 = livello 2 (m, ft)
h1 = livello 1 (m, ft)
(3) può essere trasformata in:
Δp = p1 – p2
= γ (h2 – h1) (4)
o
p1 – p2 = γ Δh (5)
dove
Δh = h2 – h1 = differenza di quota – la profondità dalla posizione h2 alla h1 (m, ft)
o
p1 = γ Δh + p2 (6)
Esempio – Pressione in un fluido
La pressione assoluta a 10 m di profondità può essere calcolata come:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 o Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
dove
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = pressione in superficie = pressione atmosferica = 101,3 kPa
La pressione relativa può essere calcolata impostando p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
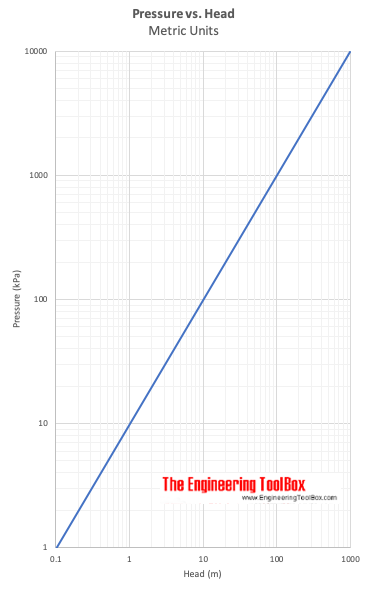
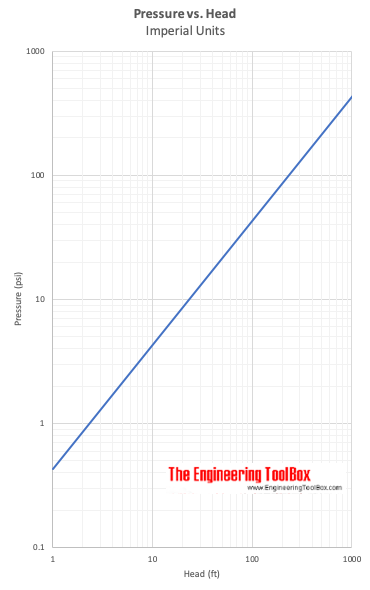
Pressure vs. Head
(6) può essere trasformato in:
Δh = (p2 – p1) / γ (7)
Δh esprimere la testa – la differenza di altezza di una colonna di fluido di peso specifico – γ – necessaria per dare una differenza di pressione Δp = p2 – p1.
Esempio – Pressione vs. Testa
Una differenza di pressione di 5 psi (lbf/in2) è equivalente a testa in acqua
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11.6 ft di acqua
o testa in Mercurio
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0.85 ft di mercurio
Peso specifico di acqua è 62.4 (lb/ft3) e il peso specifico del mercurio è 847 (lb/ft3).
- Velocity – Dynamic Pressure vs. Head