Análise amortizada é usada para algoritmos que têm operações caras que só raramente acontecem.

Análise de complexidade amortizada é mais comumente usada com estruturas de dados que têm estado que persiste entre operações.A idéia básica é que uma operação cara pode alterar o estado para que o pior caso não possa ocorrer novamente por muito tempo, amortizando assim seu custo.
Deixe T1, T2, …, Tk ser as complexidades de uma seqüência de operações em uma estrutura de dados. A complexidade amortizada de uma única operação nesta sequência é(T1 + T2 + …+ Tk) / k.
Exemplo: uma matriz dinâmica
Em uma matriz dinâmica, os elementos são armazenados no início de uma matriz fixa subjacente, e as posições restantes não são utilizadas.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Aqui está uma visão da memória ao anexar os elementos 2, 7, 1, 3, 8, 4 a uma matriz inicialmente vazia com capacidade 2.
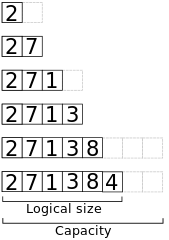
Tempo do primeiro caso
A pior complexidade de tempo para anexar um elemento a um array de comprimento n, usando este algoritmo, é Θ(n).Se o array estiver cheio, o algoritmo aloca um novo array de comprimento 2n,e então copia os elementos do array antigo para o novo.
Cleary este resultado é excessivamente pessimista.As seguintes n operações anexas serão muito mais baratas – cada uma delas será executada em tempo constante já que o novo array alocado tem espaço para todos os novos elementos.
Tempo amortizado
Uma análise de tempo amortizado dá uma compreensão muito melhor do algoritmo.
Considerar uma sequência de n operações anexas,onde começamos com um array de comprimento 1. Uma análise cuidadosa mostra que o tempo total destas operações é apenas Θ(n).
- Haverá um total de n operações de atribuição e incremento de tempo constante.
- O redimensionamento acontecerá apenas na operação 1, 2, 4, …, 2k, para um total de 1 + 2 + 4 + …+ 2k = 2-2k – 1 operações de cópia de elemento de tempo constante. Desde 2k ≤ n, isto é no máximo 2n – 1.
Hence, a complexidade de tempo amortizado para uma única operação de apêndice é Θ(1).
Mais sobre análise de algoritmo

Complexidade de tempo: Conte seus passos

Big O notation