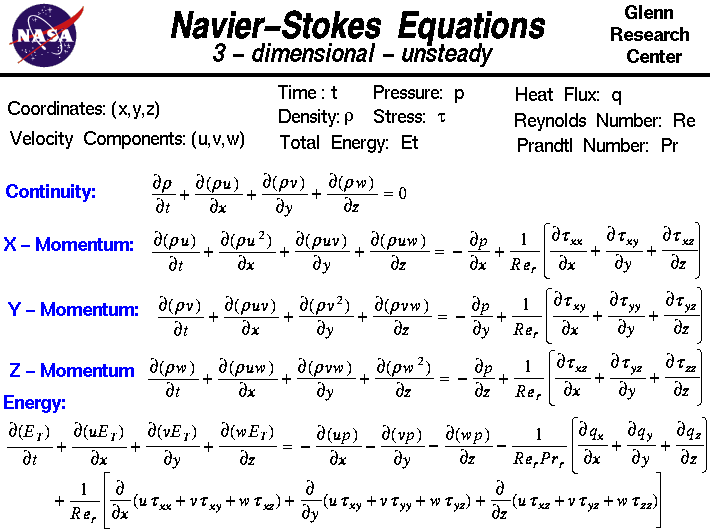
Neste slide mostramos a forma tridimensional instável das Equações de Navier-Stokes. Estas equações descrevem como a velocidade, pressão, temperatura e densidade de um fluido em movimento estão relacionadas. As equações foram derivadas independentemente por G.G. Stokes, inEngland, e M. As equações são extensões das Equações de Euler e incluem os efeitos da viscosidade sobre o fluxo. Estas equações são muito complexas, mas os estudantes de engenharia são ensinados a derivá-las em um processo muito semelhante à derivação que apresentamos na página de conservação do momentumweb.
As equações são um conjunto de equações diferenciais acopladas e poderiam, em teoria, ser resolvidas para um determinado problema de fluxo usando métodos de cálculo, mas, na prática, estas equações são muito difíceis de resolver analiticamente. No passado, os engenheiros fizeram mais aproximações e simplificações ao conjunto de equações até que tivessem um grupo de equações que pudessem resolver.Esta área de estudo é chamada Dinâmica dos Fluidos Computacional ou CFD.
As equações de Navier-Stokes consistem de uma equação de continuidade dependente do tempo para a conservação da massa,três variáveis dependentes do tempo para a conservação deumequações de momento e uma equação de energia dependente do tempo. Há seis variáveis dependentes; a pressão p, densidade r e temperatura T (que está contida na equação energética através da energia total Et) e três componentes do vetor velocidade; o componente u está no sentido x, o componente v está no sentido y e o componente w está no sentido z, todas as variáveis dependentes são funções de todas as quatro variáveis independentes.As equações diferenciais são, portanto, equações diferenciais parciais e não as equações diferenciais comuns que você estuda na classe de cálculo abeginning.
Você notará que o símbolo diferencial é diferente do usual “d /dt” ou “d /dx” que você vê para as equações diferenciais comuns. O símbolo”
” é usado para indicar derivadas parciais. O símbolo indica que devemos manter todas as variáveis independentes fixas, exceto a variável ao lado do símbolo, ao computar a derivada. O conjunto de equações é:
Continuidade: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energia: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
where Re is theReynolds numberwhich is a similarity parameter that is the ratio of the scaling of the the the theinertia of the flow to the viscous forces in the flow. As qvariáveis são os componentes do fluxo de calor e Pr é o número Prandtl que é um parâmetro de similaridade que é a razão entre os tensores de tensão e as tensões térmicas. Nosso vetor velocidade tem três componentes; o tensor de tensão tem nove componentes. Cada componente do tensor de tensão é ele mesmo derivado dos componentes de velocidade.
Os termos no lado esquerdo das equações de momento são chamados de termos de convecção das equações.Convecção é um processo físico que ocorre num fluxo de gás no qual alguma propriedade é transportada pelo movimento ordenado do fluxo.Os termos do lado direito das equações de momento que são multiplicados pelo número inverso de Reynolds são chamados de termos de difusão.Difusão é um processo físico que ocorre em um fluxo de gás no qual alguma propriedade é transportada pelo movimento aleatório das moléculas do gás.Difusão está relacionada ao tensor de tensão e à viscosidade do gás. As equações de Euler contêm apenas o termo de convecção das equações de Navier-Stokes, não podendo, portanto, as camadas de fronteira do modelo. Há uma simplificação especial das equações de Navier-Stokesequations que descrevem fluxos de camadas limite.
Note que todas as variáveis dependentes aparecem em cada equação. Para resolver um problema de fluxo, você tem que resolver todas as cinco equações simultaneamente; é por isso que chamamos a isto um sistema acoplado de equações. Nós só mostramos cinco equações para seis incógnitas. Anequação de staterelates a pressão, temperatura e densidade do gás. E precisamos especificar todos os termos do tensor de tensão. No CFD os termos do tensor de tensão são frequentemente aproximados por um modelo turbulencemodel.
Atividades:
Atividades:
Tours guiadas
Navegação …
Guia do iniciador Página inicial