Uma camada limite é uma camada fina de fluido viscoso próximo à superfície sólida de uma parede em contato com um jato em movimento no qual (dentro de sua espessura δ) a velocidade do fluxo varia de zero na parede (onde o fluxo “cola” a parede por causa de sua viscosidade) até Ue no limite, que aproximadamente (dentro de 1% de erro) corresponde à velocidade do fluxo livre (ver Figura 1). A rigor, o valor de δ é um valor arbitrário porque a força de atrito, dependendo da interação molecular entre o fluido e o corpo sólido, diminui com a distância da parede e torna-se igual a zero no infinito.
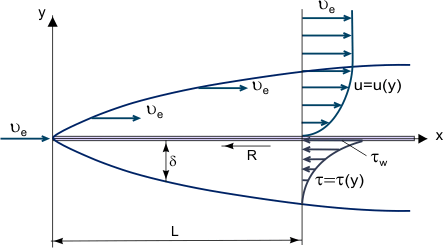
Figure 1. Crescimento de uma camada limite em uma placa plana.
O conceito fundamental da camada limite foi sugerido por L. Prandtl (1904), ele define a camada limite como uma camada de fluido se desenvolvendo em fluxos com Reynolds Numbers Re muito altos, isto é, com viscosidade relativamente baixa em comparação com as forças de inércia. Isto é observado quando os corpos são expostos à corrente de ar de alta velocidade ou quando os corpos são muito grandes e a velocidade da corrente de ar é moderada. Neste caso, em uma camada limite relativamente fina, a Tensão de Corte por fricção (força de cisalhamento viscoso): τ = η (onde η é a viscosidade dinâmica; u = u(y) – “perfil” do componente de velocidade longitudinal da camada limite, ver Figura 1) pode ser muito grande; em particular, na parede onde u = 0 e τw = ηw embora a viscosidade em si possa ser bastante pequena.
É possível ignorar as forças de atrito fora da camada limite (em comparação com as forças de inércia), e com base no conceito de Prandtl, considerar duas regiões de escoamento: a camada limite onde os efeitos de atrito são grandes e o núcleo quase invisível do escoamento. Com base na premissa de que a camada limite é uma camada muito fina (δ << L, onde L é a dimensão linear característica do corpo sobre o qual ocorre o fluxo ou o canal contendo o fluxo, sua espessura diminuindo com o crescimento de Re, Figura 1), pode-se estimar a ordem de grandeza da espessura da camada limite a partir da seguinte relação:
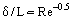
Por exemplo, quando um avião voa a Ue = 400 km/h, a espessura da camada limite na borda de fuga da asa com um acorde de 1 metro (comprimento do perfil) é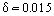 m. Como foi estabelecido experimentalmente, uma camada de limite laminar desenvolve-se na secção de entrada do corpo. Gradualmente, sob a influência de alguns fatores desestabilizadores, a camada limite torna-se instável e ocorre a transição da camada limite para um regime de Turbulent Flow. Investigações experimentais especiais estabeleceram a existência de uma região de transição entre as regiões turbulentas e laminares. Em alguns casos (por exemplo, em alto nível de turbulência do fluxo externo), a camada limite se torna turbulenta imediatamente abaixo do ponto de estagnação do fluxo. Em algumas condições, tais como uma queda de pressão severa, um fenômeno inverso ocorre na aceleração dos fluxos turbulentos, nomeadamente a relaminarização do fluxo.
m. Como foi estabelecido experimentalmente, uma camada de limite laminar desenvolve-se na secção de entrada do corpo. Gradualmente, sob a influência de alguns fatores desestabilizadores, a camada limite torna-se instável e ocorre a transição da camada limite para um regime de Turbulent Flow. Investigações experimentais especiais estabeleceram a existência de uma região de transição entre as regiões turbulentas e laminares. Em alguns casos (por exemplo, em alto nível de turbulência do fluxo externo), a camada limite se torna turbulenta imediatamente abaixo do ponto de estagnação do fluxo. Em algumas condições, tais como uma queda de pressão severa, um fenômeno inverso ocorre na aceleração dos fluxos turbulentos, nomeadamente a relaminarização do fluxo.
Apesar da sua relativa finura, a camada limite é muito importante para iniciar processos de interação dinâmica entre o fluxo e o corpo. A camada limite determina o arrastamento aerodinâmico e a elevação do veículo voador, ou a perda de energia para o fluxo de fluido em canais (neste caso, uma camada limite hidrodinâmica porque também existe uma camada limite térmica que determina a interação termodinâmica da Transferência de Calor).
O cálculo dos parâmetros da camada limite é baseado na solução das equações obtidas das equações de Navier-Stokes para o movimento do fluido viscoso, que são primeiro consideravelmente simplificadas tendo em conta a finura da camada limite.
A solução sugerida por L. Prandtl é essencialmente o primeiro termo de expansão da série de potências da equação de Navier-Stokes, sendo a expansão da série realizada para potências de parâmetro sem dimensão (δ/L). O parâmetro menor neste termo está em potência zero, de modo que a equação da camada limite é a aproximação zero em uma expansão assimptótica (em grande Re) da equação da camada limite (solução assimptótica).
Uma transformação da equação de Navier-Stokes em equações da camada limite pode ser demonstrada derivando a equação de Prandtl para camada limite laminar num fluxo bidimensional incompressível sem forças do corpo.
Neste caso, o sistema de equações de Navier-Stokes será:

Após avaliar a ordem de magnitude de alguns termos de Eq. (2) e ignorando pequenos termos, o sistema de equações de Prandtl para a camada limite laminar torna-se:

>
em que x, y são as coordenadas longitudinais e laterais (Figura 1); v é a componente velocidade ao longo do eixo “y”; p, pressão; t, tempo; e n a viscosidade cinemática.
A camada limite é fina e a velocidade na sua borda externa Ue pode ser suficiente e precisamente determinada como a velocidade de um fluxo de fluido ideal (invisível) ao longo da parede calculada até à primeira aproximação, sem ter em conta a acção inversa da camada limite sobre o fluxo externo. O gradiente de pressão longitudinal = (em p(y) = constante) em Eq. (3) pode ser retratado a partir da equação de Euler do movimento de um fluido ideal. Do acima exposto, as equações de Prandtl na sua forma finita serão escritas como:

Este é um sistema de equações parabólicas, não lineares diferenciais parciais de segunda ordem, que são resolvidas com condições iniciais e limites


O sistema de equações (4) é escrito para valores reais dos componentes de velocidade u e v. Para generalizar as equações obtidas para escoamento turbulento, deve ser usada a conhecida relação entre os componentes reais, médios e pulsantes dos parâmetros de escoamento turbulento. Por exemplo, para componentes de velocidade existem relações conectando componentes reais u e v, média ū e e componentes pulsantes u’ e v’:
e componentes pulsantes u’ e v’:

Após alguns rearranjos, é possível obter outro sistema de equações do sistema (3), em particular para fluxo estável:
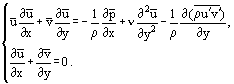
Usando a seguinte relação para a tensão de cisalhamento de atrito na camada limite:
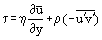
e tendo em conta que na camada limite laminar u = u’ e é possível reescrever as equações de Prandtl de uma forma válida tanto para fluxos laminares como turbulentos:
é possível reescrever as equações de Prandtl de uma forma válida tanto para fluxos laminares como turbulentos:
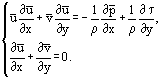
As soluções mais simples foram obtidas para uma camada de contorno laminar sobre uma fina placa plana num fluxo paralelo bidimensional de fluido incompressível (Figura 1). Neste caso, a estimativa da ordem de grandeza dos termos das equações: x ~ L, y ~ δ, δ ~ permite combinar as variáveis x e y numa relação
permite combinar as variáveis x e y numa relação

e reduzir a solução de Eq. (8) (em dp/dx = 0) para determinar as dependências de u e v sobre o novo parâmetro ξ. Por outro lado, usando relações bem conhecidas entre os componentes de velocidade u, v e a função stream ψ

é possível obter uma equação diferencial ordinária não linear da terceira ordem, em vez do sistema de equações diferenciais parciais (8)

>
Aqui, f(ξ) é a função desconhecida da variável ξ: f = ƒ =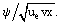
A primeira solução numérica de Eq. (10) foi obtida por Blasius (1908) sob condições de contorno correspondentes às condições físicas da camada limite em y = 0: u = 0, v = 0; em y → ∞; u → Ue (camada limite de Blasius).
Figure 2 compara os resultados da solução Blasius (linha sólida) com os dados experimentais. Usando esses dados, é possível avaliar a espessura da camada limítrofe viscosa. Em ξ  2,5, (u/Ue
2,5, (u/Ue 0,99) (Figura 2); consequentemente de Eq. (9) obtemos:
0,99) (Figura 2); consequentemente de Eq. (9) obtemos:

Figure 2.
Do cálculo numérico Blasius do valor da segunda derivada da função f(ξ) na tensão de corte de fricção da parede, a relação neste caso é:

Força de fricção R, atuando em ambos os lados da placa de comprimento L (Figura 1), também é determinada a partir de Eq. (11):
 >
>>
como no coeficiente de atrito para placas planas:
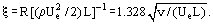 >
>>
>
Embora as equações de Prandtl sejam muito mais simples que as equações de Navier-Stokes, as suas soluções foram obtidas para um número limitado de problemas. Para muitos problemas práticos, não é necessário determinar perfis de velocidade na camada limite, apenas espessura e tensão de corte. Este tipo de informação pode ser obtida resolvendo a equação de momento integral

>
A relação integral (12) é válida tanto para a camada limite laminar como para a camada limite turbulenta.
Funções que não eram conhecidas a priori mas que caracterizam a distribuição dos parâmetros do fluido através da espessura da camada δ estão sob a integral em Eq. (12). E o erro de cálculo da integral é menor que o erro na função aproximadamente assumida integrand ρu = ρu(y). Isto cria condições para desenvolver métodos aproximados de cálculo dos parâmetros da camada limite que consomem menos tempo do que os métodos exatos de integração das equações Prandtl. O conceito fundamental foi primeiramente sugerido por T. von Karman, que introduziu tal espessura arbitrária de camada δ*
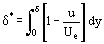
e espessura de deslocamento de momento δ***
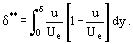
thus, podemos transformar Eq. (12) para camada limite bidimensional de fluido incompressível para:

Existem três funções desconhecidas em Eq. (15), a saber, δ* = δ*(x), δ*** = δ**(x) e τw = τw(x) .
A solução de uma equação diferencial comum como Eq. (15) geralmente requer a suposição (ou representação) da distribuição da velocidade (perfil de velocidade) através da espessura da camada limite como função de alguns parâmetros característicos (parâmetros de forma), e também requer a utilização de dados empíricos sobre a relação entre o coeficiente de atrito Cf = 2τw/(ρU2e) e a espessura arbitrária da camada limite (lei de atrito).
Algumas explicações físicas definidas podem ser dadas no que diz respeito aos valores de δ* e δ***. A função integrand em Eq. (13) contém após o rearranjo, um termo (Ue – u) que caracteriza a diminuição da velocidade. A integral em Eq. (14) pode assim ser considerada como uma medida de diminuição do caudal através da camada limite, em comparação com o caudal de fluido perfeito à velocidade Ue. Por outro lado, o valor de δ* pode ser considerado como a medida do desvio ao longo de uma parede normal (ao longo do eixo “y”) da linha de fluxo externo sob a influência de forças de atrito. A partir desta consideração da estrutura integral de Eq. (14), é possível concluir que δ** caracteriza a diminuição do momento na camada limite sob a influência do atrito.
As seguintes relações são válidas:

onde H é o parâmetro forma do perfil de velocidade da camada limite. Por exemplo, para a distribuição linear u = ky,
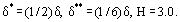
>
Actualmente, as chamadas teorias semi-empíricas são amplamente utilizadas para prever os parâmetros da camada limite turbulenta. Neste caso, assume-se que a tensão de atrito total τ em uma camada limite turbulenta é uma soma

Aqui, τT é tensão de atrito adicional (turbulenta ou Reynolds), em particular, em um fluxo incompressível ver Eq. (7).
ver Eq. (7).
Esta representação está directamente ligada ao sistema de equações de movimento na camada limite (6). Na camada limite compressiva, as pulsações de densidade podem ser consideradas como o resultado de pulsações de temperatura

where β = (1/T) é o coeficiente de expansão volumétrica.
Hipóteses semi-empíricas adicionais sobre transferência de momento turbulento são usadas para determinar τT. Por exemplo,

>
where ηT é o coeficiente dinâmico de viscosidade turbulenta introduzido por J. Boussinesq em 1877.
Na base do conceito de similaridade de troca molecular e turbulenta (teoria da similaridade) Prandtl introduziu a hipótese do comprimento de mistura (die Mischungsweg). O comprimento de mistura 1 é o caminho pelo qual um volume de fluido finito (“mole”) passa de uma camada de movimento médio para outra sem alterar o seu momento. De acordo com esta condição, ele derivou uma equação que provou ser fundamental para a teoria da camada limite:

Para a região turbulenta da camada limite do fluxo próximo à parede, L. Prandtl considerou o comprimento 1 proporcional a y

onde κ é uma constante empírica.
Fechar à parede, onde ηT << η, a fricção molecular viscosa é um factor determinante. A espessura desta parte da camada limite δ1, que é conhecida como subcamada laminar ou viscosa, é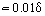 . Fora da subcamada, o valor de ηT aumenta, atingindo várias ordens de grandeza maior do que η. Correspondentemente, nesta zona da camada limite conhecida como núcleo turbulento τT > 0 = η. Algumas vezes o núcleo turbulento é subdividido na zona tampão, onde o atrito laminar e turbulento são o valor comparável, e a zona desenvolvida, onde τT >> τ0. Para esta região, após integrar Eq. (18) e levando em conta Eq. (19), é possível derivar uma expressão para perfil de velocidade logarítmica:
. Fora da subcamada, o valor de ηT aumenta, atingindo várias ordens de grandeza maior do que η. Correspondentemente, nesta zona da camada limite conhecida como núcleo turbulento τT > 0 = η. Algumas vezes o núcleo turbulento é subdividido na zona tampão, onde o atrito laminar e turbulento são o valor comparável, e a zona desenvolvida, onde τT >> τ0. Para esta região, após integrar Eq. (18) e levando em conta Eq. (19), é possível derivar uma expressão para perfil de velocidade logarítmica:
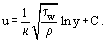
Se forem usadas coordenadas sem dimensão (ou universais).
 >
>>
>
onde é a chamada velocidade dinâmica (ou Velocidade de Atrito), Eq. (20) pode ser reescrita na seguinte forma:
é a chamada velocidade dinâmica (ou Velocidade de Atrito), Eq. (20) pode ser reescrita na seguinte forma:
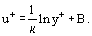
>
Representação da distribuição da velocidade em coordenadas universais e modelos matemáticos para coeficiente de viscosidade turbulenta são tratados com mais detalhes na seção de Fluxo Turbulento.
Uma das versões atuais da teoria semi-empírica da camada limite turbulenta desenvolvida por S. S. Kutateladze e A. I. Leontiev baseia-se na chamada teoria assimptótica das camadas limite turbulentas em Re → ∞ onde a espessura da subcamada laminar (viscosa) δ1 diminui a uma taxa superior a δ como resultado do qual (δ1/δ) → 0.
Nessas condições, uma camada limite turbulenta com “viscosidade de desaparecimento” está se desenvolvendo. Nesta camada, η → 0 mas não é igual a zero e, neste aspecto, a camada difere do fluxo de fluido perfeito. O conceito de lei de atrito relativo, introduzido por S. S. Kutateladze e A. I. Leontiev (1990), indica
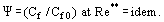
A lei é definida como a razão entre o coeficiente de atrito Cf para a condição em consideração e o valor de Cf0 para condições “standard” numa placa plana, impermeável, fluida por um fluxo incompressível, isotérmico, sendo ambos os coeficientes obtidos para Re** = Ueδ**/ν. É mostrado que em Re → ∞; η → 0; e Cf → 0, a variação relativa do coeficiente de atrito sob a influência de fatores perturbadores como gradiente de pressão, compressibilidade, não-isotermicidade, injeção (sucção) através de uma parede porosa etc., tem um valor finito.
As equações derivadas para o cálculo do valor de Ψ têm uma característica importante que torna Ψ independente de constantes empíricas de turbulência. De acordo com o conceito fundamental da “abordagem” integral, a equação de momento integral é transformada em:
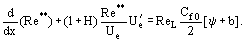
Here, ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) são os parâmetros de permeabilidade para o caso de injecção de um gás à densidade ρw através de uma parede permeável à velocidade de vw. Para determinar a função Re** = Re***
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) são os parâmetros de permeabilidade para o caso de injecção de um gás à densidade ρw através de uma parede permeável à velocidade de vw. Para determinar a função Re** = Re*** , é necessário calcular a distribuição
, é necessário calcular a distribuição Para este fim, aplica-se o princípio da sobreposição de fatores perturbadores
Para este fim, aplica-se o princípio da sobreposição de fatores perturbadores

Em Eq. 24, cada multiplicador representa a lei de atrito relativo, tendo em conta o efeito de um dos factores, entre eles a compressibilidade ΨM, a temperatura (ou Enthalpy) cabeça ΨT, a injecção ΨB, o gradiente de pressão ΨP e outros.
Os conceitos fundamentais da camada limite criam condições para explicar fenômenos como separação do fluxo da superfície sob a influência da inércia do fluxo, desaceleração do fluxo viscoso pela parede e gradiente de pressão adverso atuando no sentido ascendente = 0 ou < 0.
Se o gradiente de pressão for adverso na localização da superfície entre as seções ‘1-4’ (ver Figura 3), a distribuição de velocidade u = u(x,y) na camada limite muda gradualmente; tornando-se “menos cheia”, diminuindo a inclinação dos jatos de fluido que estão mais próximos da parede e possuindo menos quantidade de energia cinética (ver perfis de velocidade na Figura 3) que penetram muito a jusante na região de aumento de pressão. Em algumas seções, por exemplo a seção ‘4’, partículas fluidas que estão na linha de fluxo ‘a-a’ (linha pontilhada na Figura 3) – tendo esgotado completamente seu suprimento de energia cinética tornam-se desaceleradas (ua = 0).
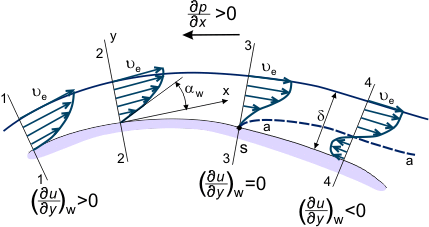
Figure 3. Camada limite no fluxo sobre uma superfície coberta.
Pressão estática e valor do gradiente de pressão não variam ao longo da espessura da camada limite. Portanto, partículas fluidas que estão mais próximas da parede do que a linha ‘a-a’ e que possuem ainda menos quantidade de energia começam a se mover na direção oposta sob a influência do gradiente de pressão na seção ‘4-4’ (ver Figura 3). Assim, a relação:

Desta forma, em alguns locais da superfície, o perfil de velocidade muda. Esta mudança é caracterizada pela alteração do sinal da derivada w de positivo (seção 2, Figura 3) para negativo (seção 4). Naturalmente, também é possível definir a seção onde w = 0 (seção 3, Figura 3). Isto é referido como a secção de separação da camada limite (correspondentemente o ponto ‘S’ na superfície desta secção é o ponto de separação). Ela é caracterizada pelo desenvolvimento de uma zona de fluxo inverso – o fluxo ao redor do corpo não é mais liso, a camada limite torna-se consideravelmente mais espessa e as linhas de fluxo externo se desviam da superfície do corpo que flui ao redor. A jusante do ponto de separação, a distribuição da pressão estática ao longo da espessura da camada não é estável e a distribuição da pressão estática ao longo da superfície não corresponde à distribuição da pressão no fluxo invisível externo.
A separação é seguida pelo desenvolvimento de zonas de fluxo inverso e redemoinhos, nos quais a energia cinética fornecida pelo fluxo externo se transforma em calor sob a influência de forças de fricção. A separação do fluxo, acompanhada pela dissipação de energia nas zonas de redemoinhos de fluxo inverso, resulta em efeitos indesejáveis como o aumento do arrasto dos veículos voadores ou perdas hidráulicas nos canais.
Por outro lado, os fluxos separados são utilizados em diferentes dispositivos para mistura intensiva de fluido (por exemplo, para melhorar a mistura de combustível e ar nas câmaras de combustão dos motores). Quando fluidos viscosos fluem em canais com secção transversal variável (gradiente de pressão alternada), a zona de separação pode ser local se a secção do difusor for seguida pela secção do confusor, onde o fluxo separado voltará a fixar-se à superfície (ver Figura 4a). Quando o fluxo se separa da borda de fuga do corpo (por exemplo, da borda de fuga da asa), a chamada esteira é formada pelas camadas de limite de “ligação” (ver Figura 4b).
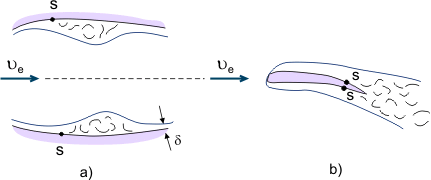
Figure 4. Fenômenos de separação das camadas de limite.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Matemática. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Matemática. Phys., 56:1-37.
Kutateladze, S. S. e Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.