- Objectivos de aprendizagem
- Redes
- Exemplo 1
- Exemplo 2
- Exercícios de revisão
- Respostas
- Prismas
- Área de superfície de um prisma usando redes
- Exemplo 3
- Exercícios de revisão
- Respostas
- Cilindros
- Área de superfície de um cilindro usando redes
- Exemplo 4
- Área de superfície de um cilindro Usando uma fórmula
- Exemplo 5
- Exemplo 6
- Exemplo 7
- Bolas
- Área de superfície de uma esfera
- Exemplo 8
- Exemplo 9
- Exercícios de revisão
- Respostas
Objectivos de aprendizagem
- Utilizar redes para representar prismas.
- Pesquisa da superfície de um prisma.
- Pesquisa da superfície de cilindros.
- Pesquisa da superfície de uma esfera.
>
Redes
Uma forma final de representar um sólido é utilizar uma rede. Se você cortar uma rede, você pode dobrá-la em um modelo de uma figura. As redes também podem ser usadas para analisar um único sólido. Aqui está um exemplo de uma rede para um cubo.
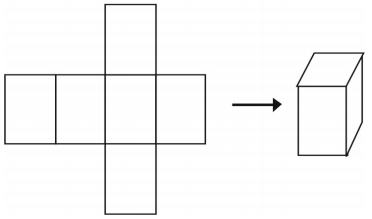
Há mais de uma maneira de fazer uma rede para uma única figura.
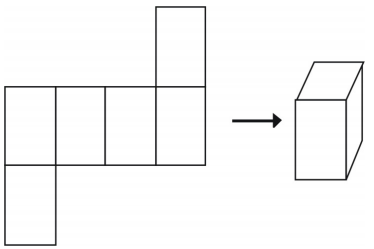
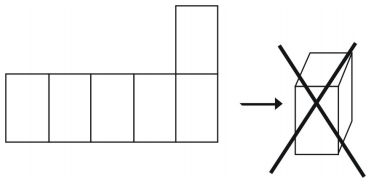
No entanto, nem todos os arranjos criarão um cubo.
Exemplo 1
>Que tipo de figura a rede cria? Desenhe a figura.
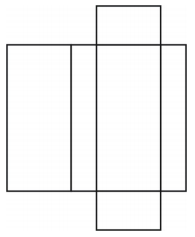
A rede cria um prisma retangular em forma de caixa, como mostrado abaixo.
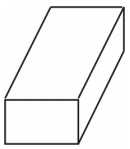
Exemplo 2
Que tipo de rede você pode desenhar para representar a figura mostrada? Desenhe a rede.
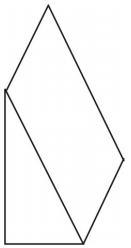
É mostrada uma rede para o prisma. Outras redes são possíveis.
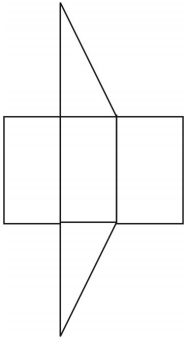
Exercícios de revisão
Desenhar uma rede para cada um dos seguintes:
Respostas
Prismas
Um prisma é uma figura tridimensional com um par de extremidades paralelas e congruentes, ou bases. Os lados de um prisma são paralelogramos. Os prismas são identificados pelas suas bases.
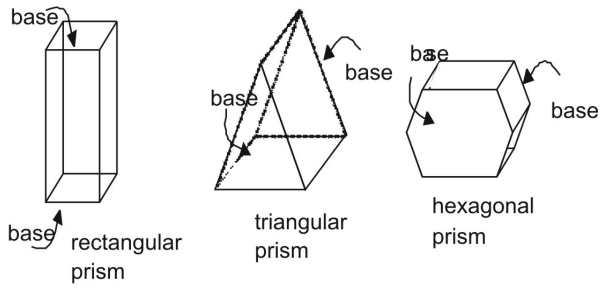
Área de superfície de um prisma usando redes
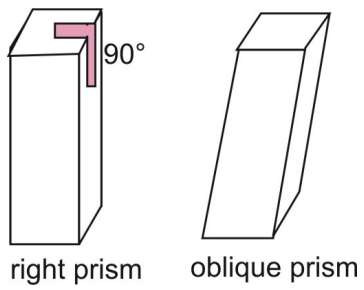
Os prismas acima são prismas certos. Em um prisma direito, os lados laterais são perpendiculares às bases do prisma. Compare um prisma direito com um oblíquo, em que os lados e bases não são perpendiculares.
Dois postulados que se aplicam à área são o Postulado de Congruência de Área e o Postulado de Adição de Área.
Possibilidade de usar uma rede e o postulado de adição de área para encontrar a área de superfície de um prisma direito.
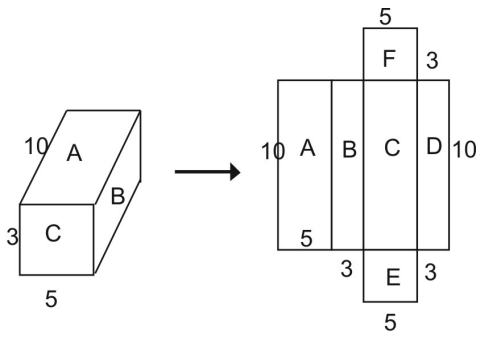
Da rede, você pode ver que a área de superfície de todo o prisma é igual à soma das figuras que compõem a rede:
Total area area = area A + area B + area C + area D + area E + area F
Usando a fórmula para a área de um retângulo, você pode ver que a área do retângulo A é:
A = l – w
A = 10 – 5 = 50 unidades quadradas
Simplesmente, as áreas dos outros rectângulos são inseridas novamente na equação acima.
Total área de superfície = área A + área B + área C + área D + área E + área F
Total área de superfície = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3)
Área total da superfície = 50 + 30 + 50 + 30 + 15 + 15
Área total da superfície = 190 unidades quadradas
Exemplo 3
Utilizar uma rede para encontrar a área da superfície do prisma.
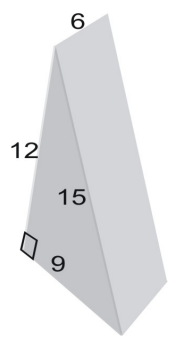
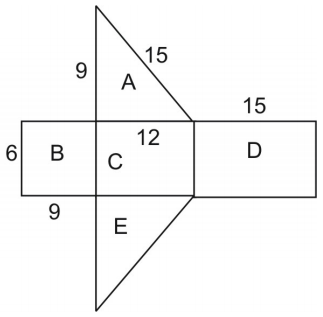
A área da rede é igual à área da superfície da figura. Para encontrar a área do triângulo, usamos a fórmula:
\displaystyle{A}==frac{1}{2}hb\\\\ onde h é a altura do triângulo e b é a sua base.
Nota que os triângulos A e E são congruentes para que possamos multiplicar a área do triângulo A por 2.
>texto estilo de exibição{area}=texto{area }A+texto{area }B+texto{area }C+texto{area }D+texto{area }E
texto estilo de exibição{ }=2(}text{area }A)+texto{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, a área de superfície é de 324 unidades quadradas.
Exercícios de revisão
Para cada um dos seguintes achados a superfície é um usando o método de redes e o perímetro
-


- A base de um prisma é um triângulo direito cujas pernas são 3 e 4 e mostram uma altura de 20. Qual é a área total do prisma?
- Um prisma hexagonal direito tem 24 polegadas de altura e tem bases que são hexágonos regulares medindo 8 polegadas de um lado. Qual é a área total da superfície?
- Qual é o volume do prisma no problema #4?
Nas perguntas seguintes, um celeiro tem a forma de um prisma pentagonal com dimensões mostradas em pés:

- Quantos pés quadrados (excluindo o telhado) existem na superfície do celeiro a ser pintado?
- Se um galão de tinta cobrir 250 pés quadrados, quantos galões de tinta são necessários para pintar o celeiro?
- Uma caixa de cartão é um cubo perfeito com uma borda de 17 polegadas. Quantos pés cúbicos pode suportar?
- Uma piscina tem 16 pés de largura, 32 pés de comprimento e tem uma profundidade uniforme de 4 pés. Quantos pés cúbicos de água consegue aguentar?
- A caixa de cereais tem 25 cm de comprimento, 9 cm de largura e 30 cm de altura. Quantos cereais aguenta?
Respostas
Redes e perímetro:
- 40.5 in2
- 838 cm2
- 252 unidades quadradas
- 1484.6 unidades quadradas
- 3990,7 polegadas cúbicas
O celeiro:
- 2450 pés quadrados
- 10 galões de tinta
- 2,85 pés cúbicos (tenha cuidado aqui. As unidades no problema são dadas em polegadas, mas a pergunta pede por pés.)
- 2048 pés cúbicos
- 6750 cm3
Cilindros
Um cilindro é uma figura tridimensional com um par de extremidades circulares paralelas e congruentes, ou bases. Um cilindro tem um único lado curvado que forma um retângulo quando disposto de forma plana.
Como com prismas, os cilindros podem ser direitos ou oblíquos. O lado de um cilindro direito é perpendicular às suas bases circulares. O lado de um cilindro oblíquo não é perpendicular às suas bases.
Área de superfície de um cilindro usando redes
É possível desconstruir um cilindro em uma rede.
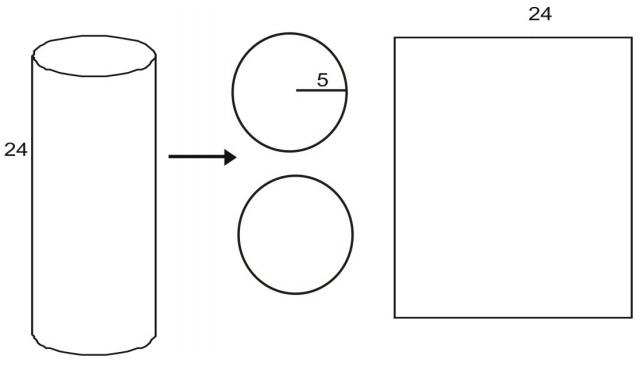
A área de cada base é dada pela área de um círculo:
A=\pi{r} ^2\\\\\\\\\\\i(5)^2\\i(5)^3543>A=25\i(25)(3.14)=78.5\\i(25)(3.14)=78.5\i(7.14)=78.5\i(7.14)=78.5\i(7.14)=78.5\i(7.14)=78.5\i(7.14)=78.5\i(7.14)=4518>A área da área lateral rectangular L é dada pelo produto de uma largura e altura. A altura é dada como 24. Você pode ver que a largura da área é igual à circunferência da base circular.
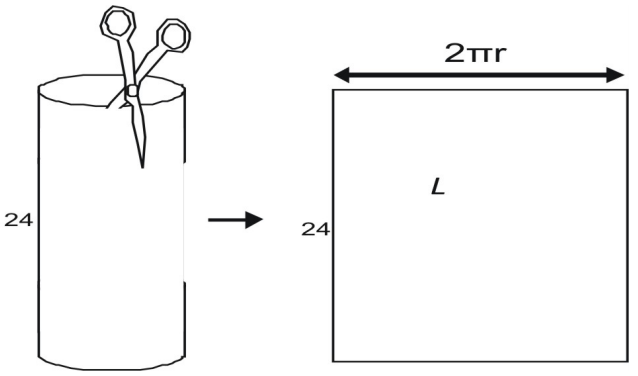
Para encontrar a largura, imagine separar um cilindro parecido com uma lata com uma tesoura. Quando você corta a área lateral, você vê que ela é igual à circunferência do topo da lata. A circunferência de um círculo é dada por C = 2πr, a área lateral, L, é
L=2{\pi}rh=3543>L=2{\pi}(5)(24){\pi}
L=240\pi}
L=approx(240)(3.14)=753.6\\\
Agora podemos encontrar a área de todo o cilindro usando A = (área de duas bases) + (área do lado lateral).
A=2(75.36)+753.6\\\\
A=904.32\\\
Vemos que a fórmula que usamos para encontrar a área total da superfície pode ser usada para qualquer cilindro direito.
Exemplo 4
Utilizar uma rede para encontrar a área de superfície do cilindro.
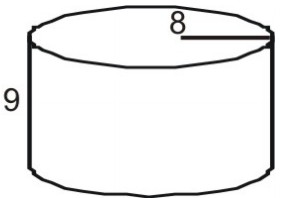
Primeiro desenho e etiqueta uma rede para a figura.
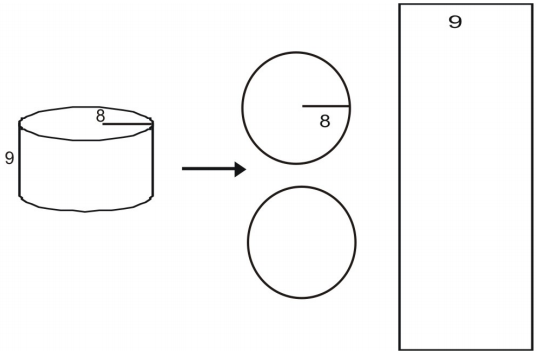
Calcular a área de cada base.
A=\pi{r}^2\\\\\
A=\pi(8)^2\\\\i(8)^3543>A=64\i(3)>A\i(64)14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\\\\\\\i
Veja a área de todo o cilindro.
A=2(200.96)+452.16\\i
A=854.08\\\\\76>
Assim, a área total de superfície é aproximadamente 854,08 unidades quadradas
Área de superfície de um cilindro Usando uma fórmula
Você viu como usar redes para encontrar a área total de superfície de um cilindro. O postulado pode ser quebrado para criar uma fórmula geral para todos os cilindros certos.
A = 2B + L

Note que a base, B, de qualquer cilindro é: B = πr2
A área lateral, L, de qualquer cilindro é:
L=texto{largura da área lateral}}cdot{altura do cilindro}
L=texto{circunferência da base}cdot{altura do cilindro}
L=2{r}cdot{h}
Pondo as duas equações juntas, obtemos:
Factoring out a from the equation gives:
The Surface Area of a Right Cylinder: Um cilindro direito com raio r e altura h pode ser expresso como:
A = 2πr2 + 2πrh
ou:
A = 2πr(r + h)
Pode usar as fórmulas para encontrar a área de qualquer cilindro direito.
Exemplo 5
Utilizar a fórmula para encontrar a área da superfície do cilindro.
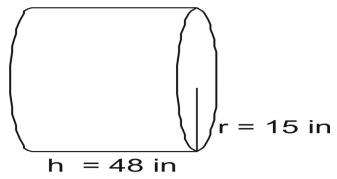
Escrever a fórmula e substituir nos valores e resolver.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\texto (polegadas quadradas)
Exemplo 6
Veja a área da superfície do cilindro.
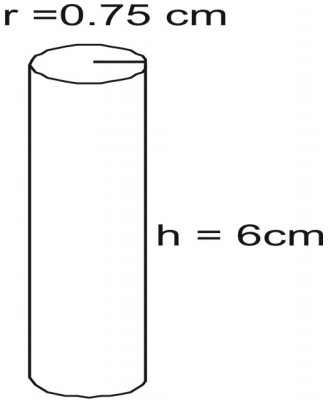
Escreva a fórmula e substitua nos valores e resolva.
A=2\pi{r}(r+h)\\\\
A=2(3.14)(0.75)\\
A=31.7925\texto (polegadas quadradas)
Exemplo 7
Perguntar a altura de um cilindro com raio de 4cm e superfície de 226,08 cm2.
Escrever a fórmula com a informação dada e resolver para h.
A=2\pi{r}(r+h)
226.08=2(3.14)(4)}
226.08=25.12\\\\
226.08=100.48+25.12h\\\
5=h\\
Bolas
Uma esfera é uma figura tridimensional que tem a forma de uma bola.

As esferas podem ser caracterizadas de três maneiras.
- Uma esfera é o conjunto de todos os pontos que se encontram a uma distância fixa r de um único ponto central O.
- Uma esfera é a superfície que resulta quando um círculo é rodado sobre qualquer um de seus diâmetros.
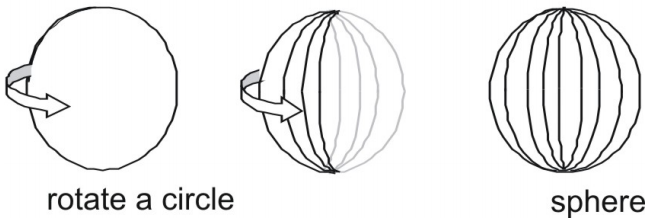
Área de superfície de uma esfera
Você pode inferir a fórmula para a área de superfície de uma esfera tomando medidas de esferas e cilindros. Aqui mostramos uma esfera com raio 3 e um cilindro direito com raio e altura 3 e expressamos a área em termos de π.
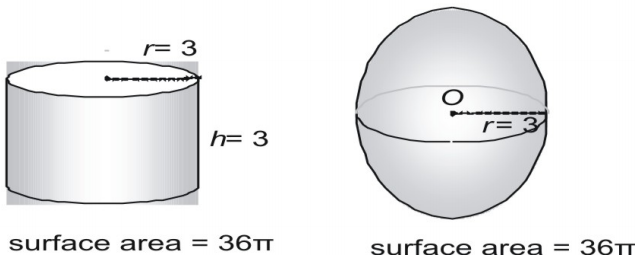
Tente agora um par maior, expressando a área de superfície em forma decimal.
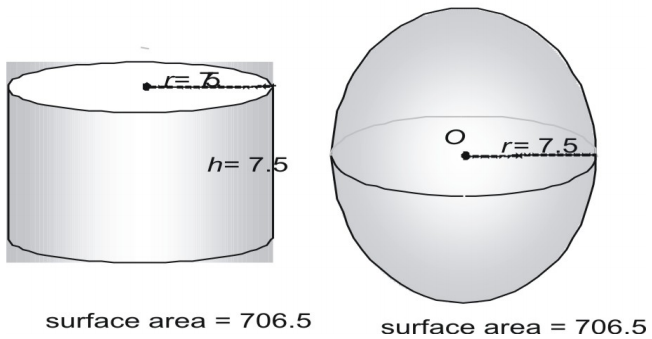
Vejam um terceiro par.
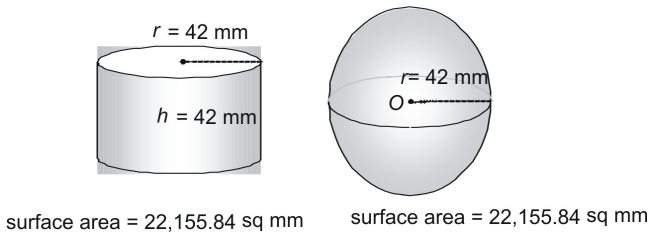
É coincidência que uma esfera e um cilindro cujo raio e altura são iguais ao raio da esfera tenham exatamente a mesma área de superfície? De modo algum! Na verdade, os antigos gregos utilizavam um método que mostrava que a seguinte fórmula pode ser usada para encontrar a área de superfície de qualquer esfera (ou qualquer cilindro em que ).
>
Exemplo 8
Pesquisa da área de superfície de uma esfera com um raio de 14 pés.
Utilizar a fórmula.
A=4\pi{r}^2\\\\i(14)^2\i(14)^2\i(196)
A=4\pi(196)}
A=784\pi(3543>2461.76\texto (pés quadrados usando }3.14\texto (para }\pi
Exemplo 9
Veja a área de superfície da figura seguinte em termos de π.
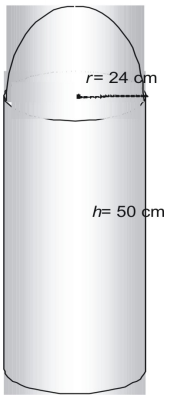
A figura é feita de uma meia esfera ou hemisfério, e um cilindro sem o seu topo.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half esfera})=2\pi(576)
A(\i(meia esfera))=1152\i(cm quadrados)
Agora encontre a área do cilindro sem o seu topo.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, a superfície total é de 1152\pi+2976\pi=4128\pi=7676>
Exercícios de revisão
- Passar o raio da esfera que tem um volume de 335 cm3.
- Determinar a área de superfície e volume desta forma:

- O raio de uma esfera é 4. Encontrar o seu volume e área de superfície total.
- Uma esfera tem um raio de 5. Um cilindro direito, tendo o mesmo raio tem o mesmo volume. Encontre a altura e a área total de superfície do cilindro.
- Esfera: volume = 296 cm3. Encontre o Diâmetro.
- Esfera: a área de superfície é 179 em2. Encontre o Raio.
- Bolas de tênis com diâmetro de 3,5 polegadas são vendidas em latas de três. A lata é um cilindro. Suponha que as bolas toquem a lata nos lados, em cima e em baixo. Qual é o volume do espaço não ocupado pelas bolas de ténis?
- Uma esfera tem uma superfície de 36π in2. Encontre o seu volume.
- A esfera gigante, operada por uma grua, tem a forma de um hemisfério de raio = 21 polegadas. O furo é preenchido com aço quente derretido. Quando o aço é vertido em um tanque cilíndrico de armazenamento que tem um raio de 28 polegadas, o aço derretido subirá a uma altura de quantas polegadas?
Respostas
Note que estes problemas usam π não 3.14.
- 1. Raio = 4,31 cm
- Área de superfície = 706,86 cm2
Volume = 1767,15 cm3 - Volume = 268,08 unidades3
Área de superfície = 201,06 unidades2 - Altura = 20/3 unidades área total de superfície = 366,52 unidades2
- Diâmetro = 8,27cm
- Radius = 3.77 polegadas
- Volume do cilindro = 32,16π in3 volume de bolas de ténis = 21,44π in3
Volume do espaço não ocupado pelas bolas de ténis = 33,68 in3 - Volume = 113,10 in3
- Altura do aço fundido no cilindro será de 7,88 polegadas



