Sol, 18 Jun 2006
1+1=2
Whitehead e o Principia Mathematica de Russell é famoso por tirar mil páginas para provar que 1+1=2. É claro que ele também prova muitas outras coisas. Se eles quisessem provar apenas que 1+1=2, provavelmente teria ocupado apenas metade do espaço.
Principia Mathematica é um livro estranho, que vale a pena analisar de um ponto de vista histórico e matemático. Ele foi escrito por volta de 1910, e a lógica matemática estava ainda em sua infância, recém-saída da transformação trabalhada por Peano e Frege. A notação é um pouco obscura, porque a notação matemática evoluiu substancialmente desde então. E muitas das técnicas simples que agora tomamos como garantidas estão ausentes. Como um programa de computador mal escrito, muitas das partes do Principia Mathematica são códigos repetidos, seções separadas que dizem essencialmente as mesmas coisas, porque os autores ainda não aprenderam as técnicas que permitiriam que essas seções fossem combinadas em uma só.
Por exemplo, a seção ∗22, “Cálculo de Classes”, começa definindo a relação de subconjuntos (∗22.01), e as operações de união de conjuntos e setintersecção (∗22.02 e .03), o complemento de um conjunto (∗22.04), e a diferença de dois conjuntos (∗22.05). Prova então a comutatividade e associatividade da união e intersecção de conjuntos (∗22.51, .52, .57,e .7), várias propriedades como !!alpha\cap\alpha = \alpha!! (∗22.5) e similares, trabalhando até teoremas como ∗22.92: !!alpha=alpha=alpha!!!.
Secção ∗23 é “Calculus of Relations” e começa quase exatamente da mesma forma, definindo a relação de subrelação (∗23.01), e as operações de união relacional e intersecção (∗23.02 e .03), o complemento de uma relação (∗23.04), e a diferença de duas relações (∗23.05). Itlater comprova a comutatividade e associatividade da união relacional e interseção (∗23.51, .52, .57,e .7), várias propriedades como !!\alpha= \alpha! …as suas propriedades, e assim por diante, e a secção ∗24 é duplicada em ∗25 numa série de teoremas sobre a existência de relações, a relação nula!!!!!! Lambda!!, a relação universal!!!!!!!!!!!, as suas propriedades, e assim por diante.
Foi assim que Whitehead e Russell o fizeram em 1910. Como é que o faríamos hoje? Uma relação entre S e T é definida como um subconjunto de S × T e é, portanto, um conjunto. União, intersecção, diferença e as outras operações são precisamente as mesmas para as relações que para os conjuntos, porque os conjuntos de relações são conjuntos. Todos os teoremas sobre uniões e interseções de relações, como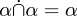 
, simplesmente desaparecem, porque já os provamos para conjuntos e as relações são conjuntos. A nullrelation é o conjunto nulo. A relação universal é o conjunto universal.
Uma enorme quantidade de outras máquinas desaparece em 2006, por causa da unificação de relações e conjuntos. O Principia Mathematica precisa de uma notação especial e uma definição tão especial para o resultado de restringir uma relação com os pêlos cujo primeiro elemento é um membro de um conjunto S particular, ou cujo segundo elemento é um membro de S, ou cujos dois elementos são membros de S; em 2006 usaríamos apenas a operação de setintersecção ordinária e falaríamos sobre R ∩(S×B) ou o que quer que seja.
Whitehead e Russell não puderam fazer isto em 1910 porque faltava uma peça de maquinaria crucial: o par encomendado. Em 1910 ninguém sabia como construir um par encomendado apenas com lógica e conjuntos. Em 2006 (ou mesmo1956), definiríamos o par encomendado <a, b> ao conjunto {{a}, {a, b}}. Então mostraríamos como ateorem que <a, b> = <c, d>if e somente se a=c e b=d, usando propriedades de conjuntos. Em seguida, definiríamos A×B como um conjunto de todos os p tais que p = <a,b> ∧ a ∈ A ∧ b∈ B. Depois definiríamos uma relação nos conjuntos A e B como um subconjunto de A×B. Depois teríamos tudo de ∗23 e ∗25 e muito de ∗33 e ∗35 e ∗36 de graça, e provavelmente muitas outras coisas também.
(A propósito, a coisa {{a}, {a, b}} foi inventada por Kuratowski. Normalmente é atribuída a Norbert Wiener, mas a idéia de Wiener, embora similar, foi na verdade mais complicada.)
Não há pares ordenados no Principia Mathematica, exceto implicitamente. Quase não existem pares. Whitehead e Russell querem basear tudo na lógica. Para Whitehead e Russell,a noção fundamental é a “função proposicional”, que é a afunção φ cuja saída é um valor de verdade. Para cada uma dessas funções, existe um conjunto correspondente, que eles denotam por !!\ que x\phi(x)!!, o conjunto de todos os xsuch que φ(x) é verdadeiro. Para Whitehead e Russell, a arelação está implícita por uma função proposicional de duas variáveis, análoga à forma como um conjunto está implícito por uma função proposicional de uma variável. Em 2006, nós dispensamos “funções de duas variáveis”, e apenas falamos de funções cujo (único) argumento é um par ordenado; uma relação então se torna o conjunto de todos os pares ordenados para o qual uma função é verdadeira.
Russell é suposto ter dito que a descoberta do Shefferstroke (um único operador lógico a partir do qual todos os outros operadores lógicos podem ser construídos) foi um tremendo avanço, e mudaria tudo. Isso nos parece estranho agora, porque a descoberta do Shefferstroke parece tão simples, e realmente não muda nada importante. Você só precisa anexar uma nota ao capítulo 1 inicial que diz que ∼p e p∨q são abreviações para p|p e p|p.|.q|q, respectivamente, provam os cinco axiomas fundamentais, e deixam tudo o resto na mesma. Mas Russellmight com alguma justiça disse a mesma coisa sobre a descoberta de que pares ordenados podem ser interpretados como conjuntos, uma simples descoberta que teria transformado o Principia Mathematica em um trabalho bem diferente.
Ainda, com esse pano de fundo no lugar, podemos discutir a provaPrincipia Mathematica de 1+1=2. Isto ocorre de forma bastante similar no Principia Mathematica, na seção ∗102. A versão Myabridged vai apenas para ∗56, mas isso é o suficiente para chegar ao importante teorema precursor, ∗54.43, escaneado abaixo:
A notação pode ser esmagadora, então vamos focar apenas no teorema, ignorar tudo o resto, até mesmo a marca de ajuda no fundo:
Este é o teorema que está a ser provado; o que se segue é o teorema à prova.
Agora eu devo explicar a notação, que mudou um pouco desde 1910. Primeiramente, o Principia Mathematica usa a notação “pontos” do Peano para desambiguar a precedência, onde agora usamos parênteses em seu lugar. A notação de pontos tem alguns que estão se acostumando, mas tem algumas vantagens distintas sobre os parênteses. A idéia é apenas que você indique o agrupamento colocando pontos, de modo que (1+2)×(3+4)×(5+6) seja escrito como1+2.×.3+4.×.5+6. A sub-fórmula do meio está entre pontos de parênteses. A sub-fórmula (1+2) está entre um par de pontos também, mas o ponto na extremidade esquerda é supérfluo, e nós omitimos; da mesma forma, a sub-fórmula (5+6) é delimitada por um ponto à esquerda e pelo final da fórmula à direita.
E se você precisar aninhar parênteses? Então você usa mais pontos. O ponto duplo (:) é como um único ponto, mas mais forte. Por exemplo, wewrite ((1+2)×3)+4 como 1+2 . × 3 : + 4, e o duplo dotisolata o 1+2 inteiro. × 3 em uma fórmula de um único ponto ao qual o +4 se aplica.
Por vezes você precisa de mais níveis de precedência, e então você usa pontos triplos (.: e :.) e quádruplos (:::). Esta fórmula, como você vê, tem pontos duplos e triplos. Traduzindo os pontos em notação de parênteses padrão, temos 54,43 dólares. \…eqiv (alfa, beta em 1)) $$. Isto é um pouco mais desorganizado do que a versão com os pontos, e fórmulas incomplicadas você pode ter problemas para descobrir quais são as parênteses que combinam com quais. Com os pontos, é sempre fácil. Então, acho que é um pouco lamentável que esta convenção tenha caído fora de uso.
O símbolo !!vdash!! não mudou; significa que a fórmula à qual se aplica é afirmada como verdadeira. !!supset!! é uma implicação lógica, e!!equiv!! é uma equivalência lógica. Λ é o conjunto vazio, que escrevemos hoje em dia como ∅. ∩ ∪ e ∈ têm os seus significados modernos: ∩ e ∪ são o cruzamento do conjunto e os unionoperators, e x∈y significa que x é o anelement do conjunto y.
Os restantes pontos são semânticos. α e β são conjuntos. 1denota o conjunto de todos os conjuntos que têm exatamente um elemento. Isto é, é o conjunto { c : existe um tal que c = {a } }. Teoremas cerca de 1 incluem, por exemplo:
- que Λ∉1 (∗52.21),
- que se α∈1 então existe algum x tal que α ={x} (∗52.1), e
- que {x}∈1 (∗52.22).
2 é de forma semelhante o conjunto de todos os conjuntos que têm exactamente dois elementos. O teorema animportante cerca de 2 é ∗54.3, que diz $$\ast54.3. \vdash 2 = o que é alfa (xexiste x)> .>x em alfa> .
Então aqui está o teorema ∗54.43 novamente:
Afirma que se os conjuntos α e β têm exatamente um elemento, então eles são desunidos (ou seja, não têm elementos incomuns) se e somente se sua união tem exatamente dois elementos.
A prova, que aparece no scan acima seguindo a palavra “Dem.”(abreviação para “demonstração”) vai assim:
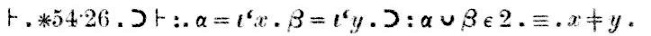
“Theorem ∗54.26implica que se α = {x} e β = {y}, thenα∪β tem 2 elementos se e somente se x é diferente de y”.
“Pelo teorema ∗51.231, este último bit (x é diferente de y) é verdadeiro se e somente se {x} e {y} sãodissociáveis”.
“Por ∗13.12, este último bit ({x} e {y} são disjoint) é verdadeiro se e somente se α e β forem disjoint”. A conclusão parcial neste ponto,que é rotulada (1), é que se α = {x} e β ={y}, então α∪β ∈ 2 se e apenas ifα∩β = Λ.
A prova continua: “A conclusão (1), com os teoremas ∗11.11 e ∗11.35, implica que se existe x e y para que α seja{x} e β seja {y}, então α∪β ∈ 2if e somente se α e β forem desjuntar”. Esta conclusão está etiquetada (2).
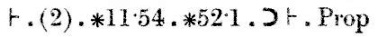
Finalmente, a conclusão (2), juntamente com os teoremas ∗11.54 e ∗52.1, implica o teorema que estávamos tentando provar.
Talvez a coisa a notar aqui seja o quão pequenos são os passos.∗54.26, dos quais este teorema depende fortemente, é quase o mesmo; afirma que {x}∪{y} ∈ 2 se e só se x≠y. ∗54.26, por sua vez, depende de ∗54.101, que diz que α tem 2 elementos se e somente se existir x andy, não o mesmo, de modo que α = {x} ∪{y}. ∗54.101 é apenas um pouco diferente da definição de 2. O teorema ∗51.231 diz que {x} e {y} são conjuntos se e apenas se x e y são diferentes.∗52.1 é uma propriedade básica de 1; vimos antes.
Os outros teoremas citados na demonstração são muito pequenos. ∗11.54 diz que você pode pegar uma asserção de que twothings existem e separá-la em duas asserções, cada uma delas afirmando que uma das coisas existe. ∗11.11 é ainda mais fino: diz que se φ(x, y) é sempre verdade, então você pode anexar um quantificador universal, e afirmar que φ(x, y) é verdadeiro para todos os x e y. ∗13.12 diz respeito à substituição de igual por igual: se x e y são iguais, então x possui uma propriedade ψ se e somente se y também for igual.
Não vi as partes posteriores do Principia Mathematica, porque minha cópia pára após a seção ∗56, e o material aritmético é muito posterior. Mas este teorema tem claramente o sentido de 1+1=2 nele, e o teorema posterior (∗110.643)que realmente afirma 1+1=2 depende muito deste teorema.
Embora eu não esteja completamente certo do que vai acontecer mais tarde(Já perdi muito tempo com isso para colocar mais tempo na versão completa da biblioteca) eu posso fazer uma adivinhação educada. O Principia Mathematica vai definir então o número 17 como sendo o conjunto de todos os conjuntos de 17 elementos, e similarmente para sempre o outro número; o uso do símbolo 2 para representar o conjunto de todos os conjuntos de 2 elementos prefigura isto. O conjunto de todos os conjuntos de elementos será então identificado como o “número cardinal”.
O Principia Mathematica irá definir a soma dos números cardinais p e qsom algo como isto: pegue um conjunto representativo a de p;a tem elementos p. Pegue um conjunto representativo bf de q; b tem elementos q. Deixe c =a∪b. Se c é um membro de algum número cardinal r, e se a e b são disjuntos, então o somatório de p e q é r.
Com esta definição, você pode provar as propriedades desejáveis habituais de adição, tais como x + 0 = x, x + y = y + x, e 1 + 1 = 2.
Em particular, 1+1=2 segue diretamente do teorema ∗54.43; é exatamente o que queremos, pois para calcular 1+1, devemos encontrar dois disjointrepresentantes de 1, e pegar seu sindicato; ∗54.43 afirma que o sindicato deve ser um elemento de 2, independentemente de qual representante escolhermos, para que 1+1=2.
Post scriptum: Peter Norvig diz que o circumflex na notaçãoPrincipia Mathematica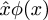 
é a fonte final do uso do wordlambda para denotar uma função anônima nas linguagens Lisp e Pythonprogramming. Tenho certeza que você sabe que estas linguagens recebem “lambda” pelo uso da letra grega λ por Alonzo Church rasgou a abstração da função em seu “λ-calculus”: Em Lisp,(lambda (u) B) é uma função que pega um argumento e retorna o valor de B; no λ-calculus,λu.B é uma função que pega um argumento e retorna o valor de B. Norvig diz que Church estava originalmente planejando escrever o functionλu.B como û.B, mas sua impressora não podia fazer acentos circunflexos. Então ele considerou mover o circunflexo para a esquerda e usar um lambda maiúsculo em vez:Λu.B. O maiúsculo Λ parecia muito parecido e ∧, o que era confuso, então ele usou letras minúsculas lambdaλ em vez.
Pós-scriptum: Todos sempre dizem “Russell and Whitehead”.Os resultados do Google para “Russell and Whitehead” superam aqueles para “Whitehead and Russell” em dois para um, por exemplo. Por quê? A capa e a página de título dizem “Alfred North Whitehead e Bertrand Russell,F.R.S.”. Como e quando é que o Whitehead perdeu na facturação superior?
link permanente