
Fern
Tady je nedávný dotaz od čtenáře Pehra ze Švédska:
Ahoj,
především, nádherné stránky. Líbí se mi.
Studoval jsem sekci polárních souřadnic v naději, že si rozšířím znalosti o rovnoramenné spirále. Interaktivní nástroje jsou skvělé, i když se mi nedaří odvodit přesné matematické řešení, proč je výsledná funkce pro zlatou spirálu
r = ae^(b(theta)).
Nějaké podklady k Pehrově otázce viz:
Polární souřadnice, křivky v polárních souřadnicích a rovnoramenná spirála
Spirály jsou v přírodě běžné a po staletí inspirovaly matematiky.

Aloe spirála

Spirální galaxie NGC 5194
Logaritmické spirály
Zlatá spirála, na kterou se Pehr ptá, je speciálním případem logaritmické spirály.
Logaritmické spirály rostou tak, že úhel přímky ze středu spirály k tečně ke křivce v tomto bodě je konstantní. Proto se jim také říká „rovnoramenné“ spirály.
Abychom si uvědomili, co to znamená, 3 ostré úhly vyznačené na následujícím obrázku kapradiny jsou přibližně 80°

Rovnoramenná kapradina
Při popisu spirál obvykle používáme funkce v polárních souřadnicích. V opačném případě, pokud použijeme obyčejné pravoúhlé souřadnice, se vzorce stávají velmi složitými.
Vzorec pro logaritmickou spirálu s použitím polárních souřadnic je:
r = aeθ cot b
kde
r je vzdálenost od počátku (nebo „pólu“)
a je konstanta
θ je úhel (v radiánech) od vodorovné osy. Souřadnice bodu na křivce v polárních souřadnicích jsou tedy dány vztahem (r, θ).
b je úhel (v radiánech – „rovný“ úhel), který svírá přímka ze středu spirály s tečnou ke spirále. Ve výše uvedeném případě kapradiny je b ≈ 1,4 radiánu (≈ 80°).
Důsledkem způsobu, jakým jsme definovali logaritmickou spirálu, je poměr vzdáleností od středu ke každému rameni sousední dvojice spirál konstantní.

Ramena spirály v konstantním poměru
Poměr
vzdálenost k prvnímu rameni: vzdálenost k druhému rameni
= 29:69
≈ 0. Z toho vyplývá, že poměr vzdáleností k prvnímu rameni je konstantní.42
Druhý poměr
vzdálenost k druhému rameni: vzdálenost k třetímu rameni
= 69:154
≈ 0,45
Vidíme, že poměry jsou téměř stejné. (Ve skutečné logaritmické spirále jsou naprosto stejné. Výběr počátečního bodu pro kapradinu není exaktní věda!)
Zlatá spirála
Zlatá spirála je speciálním případem logaritmické spirály.
Obecnou logaritmickou spirálu můžeme zapsat jako funkci v polárních souřadnicích pomocí t takto:
r(t) = aet cot b
Poznámka: Obvykle používáme pro nezávislou proměnnou θ, ale často používáme t, protože si můžeme představit, že spirálu sledujeme v čase. Kromě toho se to lépe píše!
Zlatá spirála má takovou zvláštní vlastnost, že na každou 1/4 otáčky (90° neboli π/2 v radiánech) se vzdálenost od středu spirály zvětší o zlatý řez φ = 1,6180.
Aby k tomu došlo, musí cot b nabýt hodnoty (která vychází z řešení naší funkce):
![]()
Použijeme-li tuto hodnotu a vezmeme-li jednoduchý případ, kdy a = 1, dostane naše funkce tvar:
r(t) = e0,30635t
Dále budeme používat vynikající bezplatný grafický nástroj GeoGebra.
Nastavení zlaté spirály pomocí programu GeoGebra
Pokud nyní v programu GeoGebra vykreslíme naši funkci na obyčejné pravoúhlé souřadnicové osy, dostaneme následující exponenciální křivku. Všimněte si, že s rostoucím t roste r stále rychleji (je strmější).
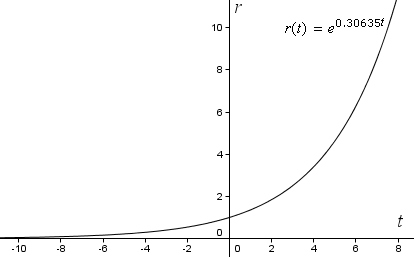
Abychom však viděli spirálu, musíme křivku vykreslit pomocí polárních souřadnic.
Pro převod polárního tvaru (který jsme získali) na obdélníkový tvar (který potřebujeme pro graf) v programu Geogebra musíme nastavit a vykreslit následující funkci:
a(t) = (r(t) cos(t), r(t) sin(t)).
Nahraďme si několik důležitých hodnot, abychom zjistili, co tento výraz znamená. Začneme-li v bodě t = 0, dostaneme počáteční bod křivky:
a(0) = (r(0) cos(0), r(0) sin(0)).
= (1×1, 1×0)
= (1, 0)
To tedy znamená, že začínáme 1 jednotku od počátku podél kladné osy x. Počáteční bod vidíte na následujícím grafu spirály.
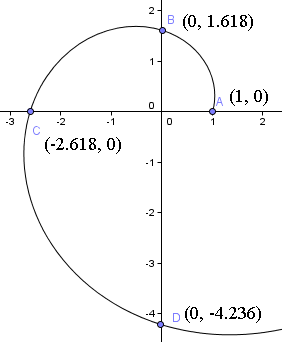
Dále se otočíme o čtvrt otáčky a zjistíme, že v bodě t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))).
= (1,618×0, 1,618×1)
= (0, 1,618)
Všimněte si, že nyní se nacházíme 1,618 jednotky od počátku po ose y nahoru. To znamená, že φ = 1,6180násobek vzdálenosti, ze které jsme vycházeli.
Dalším otočením o čtvrt otáčky se dostaneme na hodnotu t = π, kde:
a(π) = (r(π) cos(π), r(π) sin(π)).
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Jsme nyní 2,618 jednotky od počátku podél záporné osy x, neboli φ = 1,6180násobek vzdálenosti od počátku, ve které jsme byli při poslední čtvrtinové otáčce.
Poznámka:
φ2 = 2,6180
Naší další polohu, podél záporné osy y, bychom mohli zjistit prostým vynásobením této poslední hodnoty hodnotou φ = 1,6180, což nám dává:
φ3 = 4,23606…
Spirála tedy protne osu y v bodě (0, -4,236).
Jedna další čtvrtinová otáčka nás přivede na φ4 = 6,85410… jednotek podél kladné osy y, tedy (6,854, 0).
Na našem výše uvedeném grafu spirály vidíme, že tyto hodnoty jsou správné.
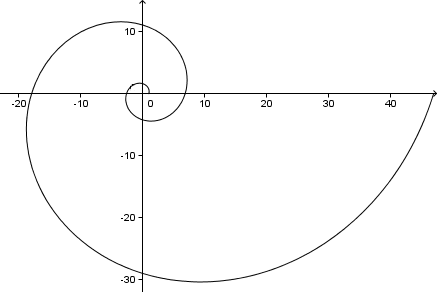
Pokud budeme pokračovat, dostaneme následující spirálu (jedná se o 2 úplné otáčky, neboli 4π = 720°):
Ještě na okraj, protože v této úloze
cot b = 0.30635
tedy
b = arccot 0,30635 = 1,274 radiánu neboli asi 73°
To je úhel, který svírají naše ramena spirály s přímkou ze středu spirály. Na výše uvedeném grafu vidíte, že každé rameno spirály svírá s osou x (a osou y nebo libovolnou přímkou od středu) úhel 73°.
Přiblížení zlaté spirály pomocí oblouků kružnice
Spirálu, která vypadá dost podobně jako zlatá spirála, můžeme získat pomocí oblouků kružnic, jejichž velikost se zvětšuje o zlatý řez, a to následujícím způsobem.
Začneme čtvercem 1×1 a nakreslíme oblouk se středem C procházející dvěma rohy tak, aby strany čtverce byly k oblouku tečné (to znamená, že se dotýkají pouze jednou).
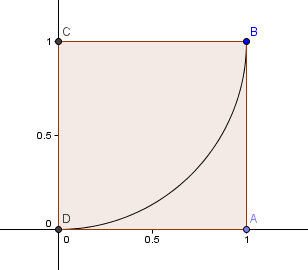
Dále umístíme čtverec o délce strany φ = 1. Na oblouk umístíme čtverec o délce strany φ = 1, který se dotýká pouze jednou.6180 nad naším prvním čtvercem a sestrojíme další kruhový oblouk se středem E jako předtím:
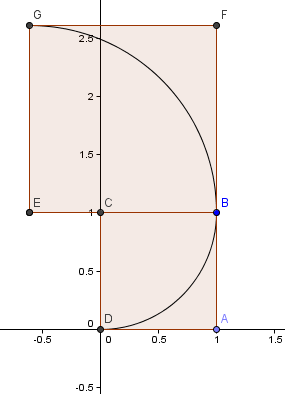
Náš další čtverec jde vlevo a má stranu φ2 = 2,6180 = 1 + φ. Je to čtverec s délkou strany φ.
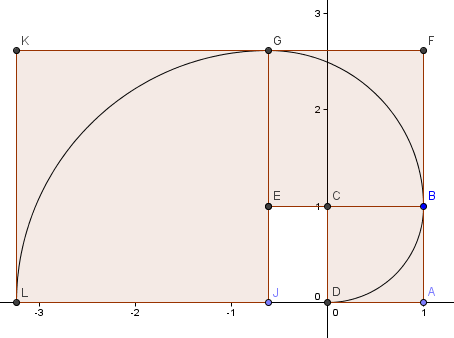
Pokračujeme ve vzoru (prošli jsme další celé kolo) a dostaneme spirálu, která se dost podobá naší Zlaté spirále z dřívějška.
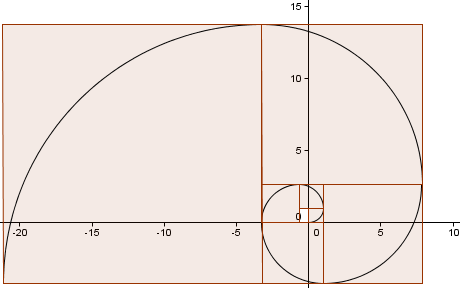
Jak blízko je naše aproximace?
V článku o Zlaté spirále na Wikipedii je obrázek, který tvrdí, že výše uvedená spirála a Zlatá spirála mají velmi blízký tvar.
Tady je ten obrázek:
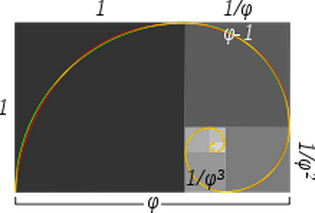
Titulek k obrázku uvádí:
Přibližná a pravá zlatá spirála: zelená spirála je vytvořena ze čtvrtkruhů tečných k vnitřku každého čtverce, zatímco červená spirála je zlatá spirála, zvláštní typ logaritmické spirály. Překrývající se části se zobrazují žlutě. Délka strany většího čtverce k následujícímu menšímu čtverci je ve zlatém řezu.
Můžeme to znovu vytvořit ?
Na obrázku níže je červená křivka první částí zlaté spirály, kterou jsme sestrojili výše, zatímco zelená křivka vychází z aproximace čtvrtoblouku, na které jsme právě pracovali.
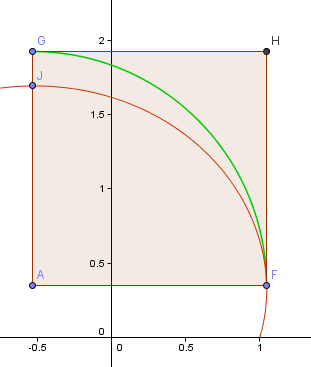
Bod F je „nejpravější“ bod na spirále, který bude mým výchozím bodem pro čtvrtoblouk. Bod J je nejvyšším bodem této části spirály.
Bod A je průsečíkem vodorovných a svislých přímek procházejících body F, respektive J, a to bude střed mého oblouku.
Nyní se oblouk GF vůbec nepřibližuje k související části spirály FJ.
Provedeme další krok a podíváme se, zda je další část lepší.
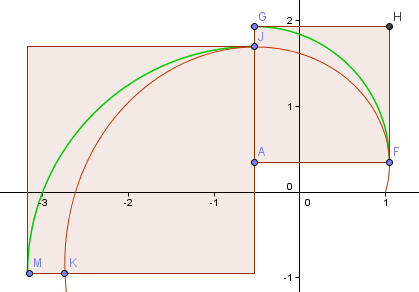
Jak vidíte, je to horší (podle očekávání, protože jsme se vzdálili od počátku a rameno spirály se zvětšuje).
Je jasné, že to nikdy nebude fungovat.
Ve své dřívější Zlaté spirále jsem však používal:
r(t) = e0,30635t
Konstanta a, měla hodnotu 1.
Chceme-li, aby naše aproximační oblouky dobře odpovídaly skutečné Zlaté spirále, musíme použít hodnotu (asi ne překvapivě)
a = φ = 1,618103399..
Tím získáme následující křivky, podobné grafu ve Wikipedii.
Červená křivka je Zlatá spirála,
r(t) = 1,618013 e0,30635t
Zelená křivka je soubor kruhových oblouků.
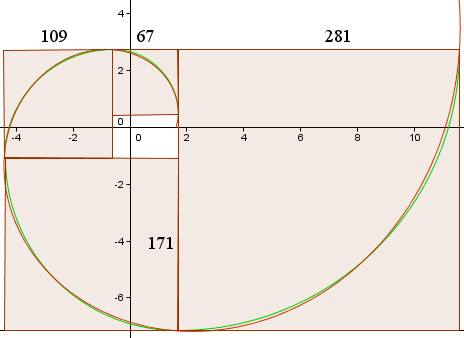
Zobrazeny jsou délky stran čtverců (v pixelech) a vidíme, že jsou přibližně v poměru 1,618013…
Zlatá spirála v médiích
Z Wolframova matematického světa:
V epizodě 4. série „Masterpiece“ (2008) kriminálního seriálu televize CBS „Myšlenky zločince“ jsou agenti jednotky FBI pro analýzu chování konfrontováni se sériovým vrahem, který používá Fibonacciho číselnou posloupnost k určení počtu obětí pro každou ze svých vražedných epizod. V této epizodě si postava doktora Reida také všimne, že místa vražd leží na grafu zlaté spirály a cesta do středu spirály umožňuje Reidovi určit místo vrahova působiště.
Tady jsou další zajímavé informace z Wolframova matematického světa:
Logaritmická spirála
Pro geeky – design pomocí zlaté spirály
Mnozí se domnívají, že designy využívající zlatý řez a zlatou spirálu jsou příjemné na pohled.
Podle zlaté spirály nedávno změnil design své hlavní stránky i Twitter.
Tady je skvělý článek od člověka, který zkonstruoval zlatou spirálu bez obrázků. (Hlavně pro ty, kteří se zajímají o webový design)
Zlatá spirála bez obrázků – pomocí CSS a jQuery
Jak v článku naznačuje, zlaté spirále je blízký i sloní chobot.

Sloní chobot – téměř Zlatá spirála
Závěr
Zlatá spirála je zajímavé téma – stojí za to se jím zabývat nejen kvůli příjemným návrhům, ale také kvůli zajímavé matematice, která za nimi stojí.
Doufám, že to pomohlo odpovědět na tvou otázku, Pehře!