
Fern
Hier volgt een recente vraag van lezer Pehr uit Zweden:
Hoi,
Ten eerste, prachtige site.
Ik heb de sectie over poolcoördinaten bestudeerd in de hoop mijn kennis over de gelijkzijdige spiraal uit te breiden. De interactieve hulpmiddelen zijn geweldig, maar ik heb moeite om de exacte wiskundige oplossing af te leiden voor de vraag waarom de resulterende functie voor de gulden spiraal
r = ae^(b(theta))
Voor enige achtergrond bij de vraag van Pehr, zie:
Polaire coördinaten, krommen in polaire coördinaten en gelijkzijdige spiraal
Spiralen komen veel voor in de natuur en hebben wiskundigen eeuwenlang geïnspireerd.

loeispiraal

Spiraalstelsel NGC 5194
Logaritmische spiralen
De Gouden Spiraal waar Pehr naar vraagt, is een speciaal geval van de logaritmische spiraal.
Logaritmische spiralen groeien zo dat de hoek van een lijn vanuit het middelpunt van de spiraal naar de raaklijn aan de kromme in dat punt constant is. Daarom worden ze ook wel “gelijkzijdige” spiralen genoemd.
Om te zien wat dit betekent, zijn de 3 scherpe hoeken die in de volgende afbeelding van de varen zijn aangegeven ongeveer 80°

Equi-hoekige varen
Wij gebruiken normaal gesproken functies in poolcoördinaten als we spiralen beschrijven. Als we anders gewone rechthoekige coördinaten gebruiken, worden de formules erg ingewikkeld.
De formule voor een logaritmische spiraal met poolcoördinaten is:
r = aeθ cot b
waar
r de afstand tot de oorsprong (of “pool”) is
a is een constante
θ is de hoek (in radialen) vanaf de horizontale as. De coördinaten van een punt op de kromme in poolcoördinaten worden dus gegeven door (r, θ).
b is de hoek (in radialen – de “gelijke” hoek) die de lijn vanuit het middelpunt van de spiraal maakt met de raaklijn aan de spiraal. In het geval van de varen hierboven is b ≈ 1,4 radialen (≈ 80°).
Als gevolg van de manier waarop we de logaritmische spiraal hebben gedefinieerd, is de verhouding van de afstanden van het middelpunt tot elke spiraalarm van een aangrenzend paar constant.

Spiraalarmen bij een constante verhouding
De verhouding
afstand tot de eerste arm: afstand tot de tweede arm
= 29:69
≈ 0.42
De andere verhouding
afstand tot de tweede arm: afstand tot de derde arm
= 69:154
≈ 0.45
We zien dat de verhoudingen bijna gelijk zijn. (In een echte logaritmische spiraal zijn ze precies hetzelfde. Het kiezen van het beginpunt voor de varen is geen exacte wetenschap)!
Gouden Spiraal
De Gouden Spiraal is een speciaal geval van de logaritmische spiraal.
We kunnen de algemene logaritmische spiraal als volgt schrijven als een functie in poolcoördinaten met t:
r(t) = aet cot b
Noot: Normaal gebruiken we θ voor de onafhankelijke variabele, maar we gebruiken vaak t omdat we kunnen denken dat de spiraal in de tijd wordt uitgetekend. Bovendien is het gemakkelijker te typen!
De gulden spiraal heeft de bijzondere eigenschap dat voor elke 1/4 draai (90° of π/2 in radialen) de afstand tot het middelpunt van de spiraal toeneemt met de gulden snede φ = 1,6180.
Om dit te laten gebeuren, moet cot b de waarde aannemen (die komt uit het oplossen van onze functie):
![]()
Gebruik makend van deze waarde, en uitgaande van het eenvoudige geval waarin a = 1, wordt onze functie:
r(t) = e0,30635t
We zullen vanaf hier het uitstekende gratis grafiekprogramma GeoGebra gebruiken.
De Gouden Spiraal opstellen met GeoGebra
Als we nu in GeoGebra onze functie op gewone rechthoekige coördinatenassen uitzetten, krijgen we de volgende exponentiële kromme. Merk op dat r steeds sneller toeneemt (hij wordt steiler) naarmate t toeneemt.
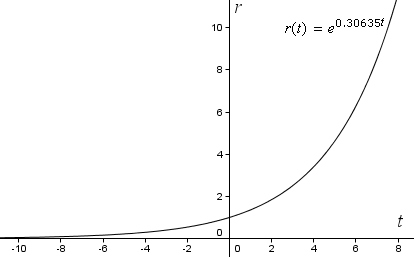
Maar om een spiraal te zien, moeten we de kromme grafisch weergeven met behulp van poolcoördinaten.
Om de poolvorm (die we hebben) om te zetten in een rechthoekige vorm (die we nodig hebben voor de grafiek) in Geogebra, moeten we de volgende functie opstellen en grafisch weergeven:
a(t) = (r(t) cos(t), r(t) sin(t))
Laten we een paar belangrijke waarden substitueren om te zien wat deze uitdrukking betekent. Beginnend bij t = 0, krijgen we het beginpunt van de kromme:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Dit betekent dus dat we 1 eenheid vanaf de oorsprong langs de positieve x-as beginnen. U kunt het beginpunt zien in de volgende grafiek van de spiraal.
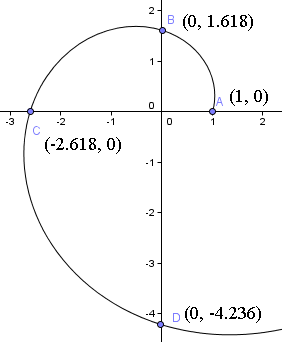
Daarna draaien we een kwartslag en vinden we op t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Merk op dat we nu 1,618 eenheden vanaf de oorsprong op de y-as staan. Dat wil zeggen, φ = 1,6180 maal de afstand van waar we begonnen.
Een volgende rotatie van een kwartslag brengt ons op t = π, waarbij:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
We zijn nu 2,618 eenheden van de oorsprong verwijderd langs de negatieve x-as, of φ = 1,6180 maal de afstand tot de oorsprong die we bij de laatste kwartslag hadden.
Note:
φ2 = 2.6180
We kunnen onze volgende positie, langs de negatieve y-as, berekenen door deze laatste waarde te vermenigvuldigen met φ = 1.6180, wat ons oplevert:
φ3 = 4.23606…
Dus de spiraal snijdt de y-as bij (0, -4,236).
Een kwartslag meer brengt ons op φ4 = 6,85410… eenheden langs de positieve y-as, dat is (6,854, 0).
We kunnen zien dat deze waarden kloppen op onze spiraalgrafiek hierboven.
Als we verder gaan, krijgen we een spiraal als volgt (dit zijn 2 volledige omwentelingen, of 4π = 720°):
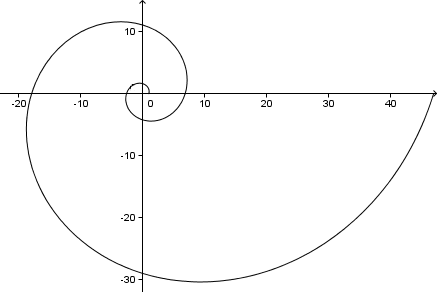
Terzijde, aangezien in dit probleem
cot b = 0.30635
dan
b = arccot 0.30635 = 1.274 radialen of ongeveer 73°
Dit is de hoek die onze spiraalarmen maken met een lijn vanuit het middelpunt van de spiraal. In de grafiek hierboven zie je dat elke spiraalarm een hoek van 73° maakt met de x-as (en y-as, of een willekeurige lijn vanuit het middelpunt).
Benaderen van de Gouden Spiraal met cirkelbogen
We kunnen een spiraal verkrijgen die erg lijkt op de Gouden Spiraal door cirkelbogen te gebruiken die in grootte toenemen met de Gulden Snede, en wel als volgt.
We beginnen met een vierkant van 1×1 en tekenen een boog, middelpunt C, door 2 hoeken zodanig dat de zijden van het vierkant raken aan de boog (dat wil zeggen dat ze elkaar slechts eenmaal raken).
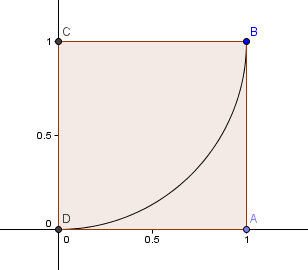
Daarna plaatsen we een vierkant met zijde lengte φ = 1.6180 boven ons eerste vierkant en construeren weer een cirkelboog met middelpunt E, zoals hiervoor:
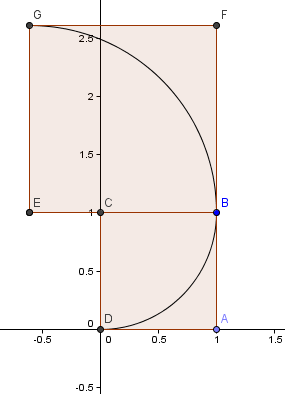
Ons volgende vierkant gaat naar links en heeft zijden φ2 = 2.6180 = 1 + φ.
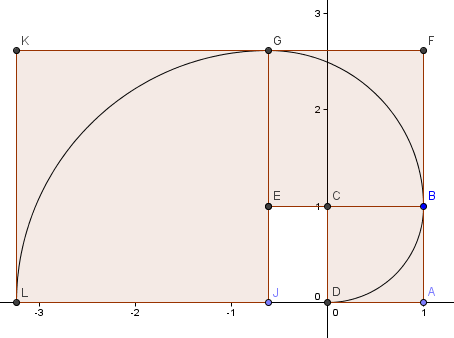
We vervolgen het patroon (we hebben weer een volledige ronde afgelegd) en krijgen een spiraal die veel lijkt op onze Gouden Spiraal van daarnet.
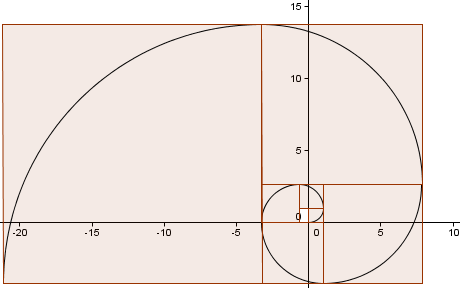
Hoe dichtbij is onze benadering?
Wikipedia’s artikel over de Gouden Spiraal heeft een afbeelding die beweert dat de bovenstaande spiraal en de Gouden Spiraal qua vorm heel dicht bij elkaar liggen.
Hier is die afbeelding:
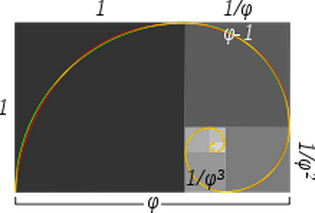
In het bijschrift bij de afbeelding staat:
Benaderde en echte gouden spiralen: de groene spiraal is gemaakt van kwartcirkels die raken aan het binnenste van elk vierkant, terwijl de rode spiraal een gouden spiraal is, een speciaal type logaritmische spiraal. Overlappende delen verschijnen geel. De lengte van de zijde van een groter vierkant tot het volgende kleinere vierkant is in de gulden snede.
Kunnen we dit nabootsen ?
In de afbeelding hieronder is de rode kromme het eerste deel van de Gouden Spiraal die we hierboven construeerden, terwijl de groene kromme gebaseerd is op de kwartdraai benadering waar we net mee bezig waren.
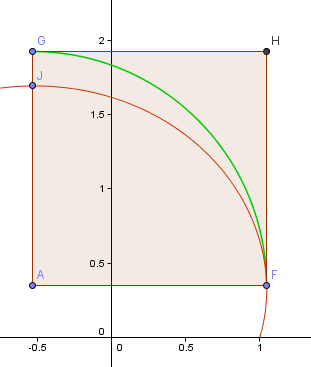
Het punt F is het “meest rechtse” punt op de spiraal, dat mijn startpunt zal zijn voor de kwartdraai boog. Het punt J is het hoogste punt van dit gedeelte van de spiraal.
Punt A is het snijpunt van de horizontale en verticale lijnen die respectievelijk door F en J gaan en dit zal het middelpunt van mijn boog zijn.
Nu ligt de boog GF helemaal niet in de buurt van het verwante gedeelte van de spiraal FJ.
Laten we nog een stap doen en kijken of het volgende deel beter is.
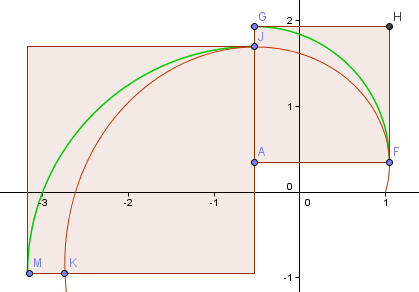
Zoals je ziet, is het slechter (zoals verwacht, want we zijn verder van de oorsprong af komen te staan en de spiraalarm wordt groter).
Het is duidelijk dat dit nooit gaat werken.
Hoewel, in mijn eerdere Gouden Spiraal gebruikte ik:
r(t) = e0.30635t
De constante a, had waarde 1.
Als we willen dat onze benaderende bogen goed passen bij de werkelijke Gulden Spiraal, moeten we een waarde gebruiken van (waarschijnlijk niet verrassend)
a = φ = 1,618103399..
Dit geeft ons de volgende krommen, vergelijkbaar met de grafiek in Wikipedia.
De rode kromme is de Gouden Spiraal,
r(t) = 1,618013 e0,30635t
De groene kromme is de verzameling van cirkelbogen.
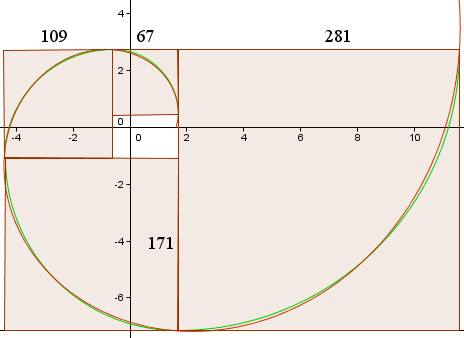
De zijlengtes van de vierkanten (in pixels) zijn weergegeven en we zien dat ze ongeveer in de verhouding 1,618013 staan…
Gouden spiraal in de media
Van Wolfram’s Mathworld:
In de aflevering “Masterpiece” (2008) van seizoen 4 van het CBS-misdaaddrama “Criminal Minds” worden de agenten van de FBI Behavioral Analysis Unit geconfronteerd met een seriemoordenaar die de getalreeks van Fibonacci gebruikt om het aantal slachtoffers te bepalen voor elk van zijn moordepisodes. In deze aflevering merkt personage Dr. Reid ook op dat de locaties van de moorden op de grafiek van een gouden spiraal liggen, en als Reid naar het midden van de spiraal gaat, kan hij de locatie van de uitvalsbasis van de moordenaar bepalen.
Hier is meer interessante informatie uit Wolfram’s Mathworld:
Logaritmische spiraal
Voor de geeks – ontwerpen met behulp van de Gulden Spiraal
Velen zijn van mening dat ontwerpen waarbij gebruik wordt gemaakt van de Gulden Snede en de Gulden Spiraal een lust voor het oog zijn.
Zelfs Twitter heeft onlangs zijn hoofdpagina opnieuw ontworpen met behulp van de Gulden Spiraal.
Hier is een geweldig artikel van een man die heeft geconstrueerd een gouden spiraal zonder afbeeldingen. (Vooral voor degenen die geïnteresseerd zijn in webdesign)
Gouden spiraal zonder afbeeldingen – met behulp van CSS en jQuery
Zoals hij suggereert in het artikel, een olifant slurf is ook dicht bij de Gouden Spiraal.

Elifantenslurf – bijna een Gouden Spiraal
Conclusie
De Gouden Spiraal is een interessant onderwerp – een die het waard is om verder te onderzoeken, niet alleen vanwege de leuke ontwerpen die erbij betrokken zijn, maar ook vanwege de interessante wiskunde erachter.
Ik hoop dat dit helpt om je vraag te beantwoorden, Pehr!