
Fern
Aqui está uma pergunta recente do leitor Pehr na Suécia:
Hi,
Primeiro de todos, site maravilhoso. Adorei.
Estive estudando a seção de coordenadas polares na esperança de expandir meus conhecimentos sobre a espiral equiangular. As ferramentas interativas são ótimas, embora eu esteja tendo dificuldade em derivar a solução matemática exata para a função resultante para a espiral dourada é
r = ae^(b(theta))
Para algum fundo sobre a pergunta de Pehr, veja:
Coordenadas Polares, Curvas em Coordenadas Polares e Espiral Equi-angular
Espirais são comuns na natureza e têm inspirado matemáticos por séculos.
>
 >
>
Espiral aloé
>
Galáxia Espiral NGC 5194
Espiral Logarítmica
A Espiral Dourada que Pehr está perguntando é um caso especial da espiral logarítmica.
As espirais logarítmicas crescem de tal forma que o ângulo de uma linha desde o centro da espiral até à tangente à curva naquele ponto é constante. Por isso também são conhecidas como espirais “equi-angulares”.
Para ver o que isto significa, os 3 ângulos agudos marcados na seguinte imagem de samambaia são aproximadamente 80°

Fambaia equi-angular
Usamos normalmente funções em coordenadas polares quando descrevemos espirais. Caso contrário, se utilizarmos coordenadas rectangulares ordinárias, as fórmulas tornam-se muito complexas.
A fórmula para uma espiral logarítmica utilizando coordenadas polares é:
r = aeθ cot b
where
r é a distância da origem (ou “pólo”)
a é uma constante
θ é o ângulo (em radianos) do eixo horizontal. Assim as coordenadas de um ponto da curva em coordenadas polares são dadas por (r, θ).
b é o ângulo (em radianos – o ângulo “igual”) que a linha do centro da espiral faz com a tangente à espiral. No caso da samambaia acima, b ≈ 1,4 radianos (≈ 80°).
Como consequência da forma como definimos a espiral logarítmica, a relação das distâncias do centro para cada braço espiral de um par adjacente é constante.

Braços espirais a uma relação constante
A relação
distância para o primeiro braço: distância para o segundo braço
= 29:69
≈ 0.42
A outra relação
distância ao segundo braço: distância ao terceiro braço
= 69:154
≈ 0.45
Vemos que as relações são quase as mesmas. (Em uma espiral logarítmica real, elas são exatamente as mesmas. Escolher o ponto de partida para o feto não é uma ciência exacta!)
Espiral Dourada
A Espiral Dourada é um caso especial da espiral logarítmica.
Podemos escrever a espiral logarítmica geral como uma função em coordenadas polares usando t da seguinte forma:
r(t) = aet cot b
Note: Normalmente, usamos θ para a variável independente, mas muitas vezes usamos t pois podemos pensar que a espiral é traçada ao longo do tempo. Além disso, é mais fácil de digitar!
A Espiral Dourada tem a propriedade especial de que para cada 1/4 de volta (90° ou π/2 em radianos), a distância do centro da espiral aumenta pela razão dourada φ = 1.6180.
Para que isso ocorra, a cot b deve tomar o valor (que vem da resolução da nossa função):
![]()
Usando este valor, e tomando o caso simples onde a = 1, a nossa função torna-se:
r(t) = e0.30635t
Usaremos a excelente ferramenta gráfica gratuita GeoGebra a partir daqui.
Configurando a Espiral Dourada usando o GeoGebra
Agora se fizermos gráficos da nossa função em eixos de coordenadas rectangulares normais no GeoGebra, obtemos a seguinte curva exponencial. Note que r aumenta a uma taxa cada vez maior (torna-se mais íngreme) à medida que t aumenta.
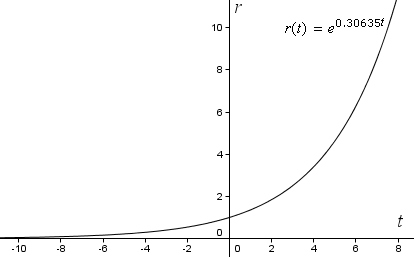
Mas para ver uma espiral, precisamos de fazer o gráfico da curva usando coordenadas polares.
Para converter a forma polar (que temos) para rectangular (que precisamos para o gráfico) na Geogebra, precisamos de configurar e fazer o gráfico da seguinte função:
a(t) = (r(t) cos(t), r(t) sin(t))
Vamos substituir alguns valores importantes para ver o que esta expressão significa. Começando em t = 0, obtemos o ponto de partida da curva:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
> Então significa que começamos 1 unidade a partir da origem ao longo do eixo x positivo. Você pode ver o ponto de partida no gráfico seguinte da espiral.
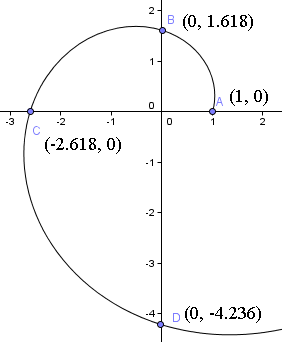
Próximo, giramos um quarto de volta e encontramos em t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Nota que agora somos 1,618 unidades da origem até o eixo y. Ou seja, φ = 1,6180 vezes a distância de onde começamos.
Uma outra rotação de um quarto de volta leva-nos a t = π, onde:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2.618×1, -2.618×0)
= (-2.618, 0)
Estamos agora a 2.618 unidades de distância da origem ao longo do eixo x negativo, ou φ = 1.6180 vezes a distância da origem que estávamos no último quarto de volta.
Nota:
φ2 = 2,6180
Podemos calcular a nossa próxima posição, ao longo do eixo y negativo, multiplicando apenas este último valor por φ = 1,6180, dando-nos:
φ3 = 4,23606…
Então a espiral irá cortar o eixo y a (0, -4,236).
Mais um quarto de volta nos levará a φ4 = 6,85410… unidades ao longo do eixo y positivo, ou seja (6,854, 0).
Podemos ver que estes valores estão correctos no nosso gráfico em espiral acima.
Se continuarmos, obteremos uma espiral da seguinte forma (isto é 2 revoluções completas, ou 4π = 720°):
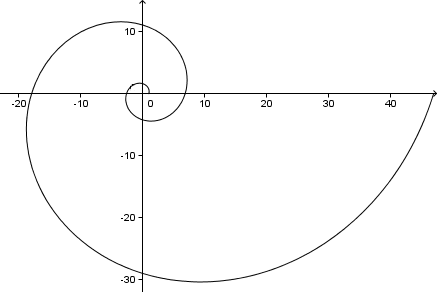
Como um aparte, já que neste problema
cot b = 0.30635
then
b = arccot 0,30635 = 1,274 radianos ou cerca de 73°
Este é o ângulo que os nossos braços espirais fazem com uma linha a partir do centro da espiral. Você pode ver no gráfico acima que cada braço espiral faz um ângulo de 73° com o eixo x (e eixo y, ou qualquer linha do centro).
Aproximando a Espiral Dourada usando arcos de um círculo
Podemos obter uma espiral que se parece bastante com a Espiral Dourada usando arcos de círculos que aumentam de tamanho pela Razão Dourada, como se segue.
Comecemos com um quadrado de 1×1 e desenhamos um arco, centro C, através de 2 cantos de forma que os lados do quadrado sejam tangentes ao arco (ou seja, tocam-se apenas uma vez).
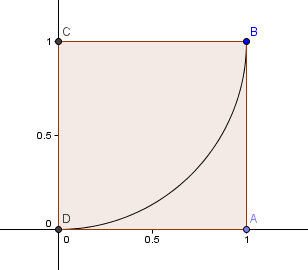
Próximo, colocamos um quadrado com comprimento lateral φ = 1.6180 acima do nosso primeiro quadrado e construímos outro arco circular, centro E, como antes:
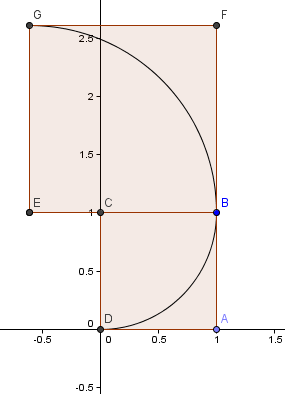
O nosso próximo quadrado vai à esquerda e tem lados φ2 = 2.6180 = 1 + φ.
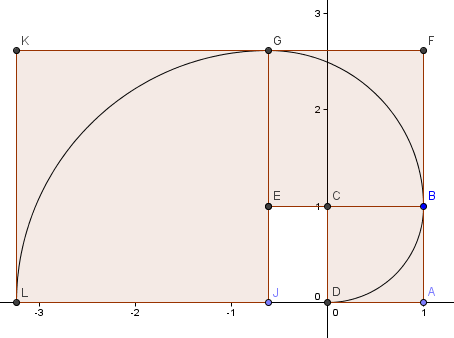
Continuamos o padrão (fomos outra volta completa) e obtemos uma espiral que se parece muito com a nossa Espiral Dourada de antes.
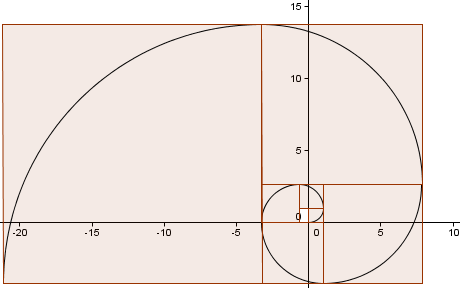
Quão perto está a nossa aproximação?
O artigo da Wikipedia sobre a Espiral Dourada tem uma imagem que afirma que a espiral acima e a Espiral Dourada estão muito próximas em forma.
Aqui está aquela imagem:
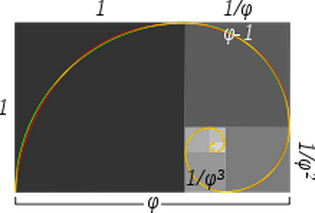
O título da imagem diz:
Espiral dourada aproximada e verdadeira: a espiral verde é feita a partir de quartos de círculo tangentes ao interior de cada quadrado, enquanto a espiral vermelha é uma espiral dourada, um tipo especial de espiral logarítmica. As porções sobrepostas aparecem amarelas. O comprimento do lado de um quadrado maior para o quadrado menor seguinte está na proporção áurea.
Podemos recriar isto ?
Na imagem abaixo, a curva vermelha é a primeira parte da Espiral Dourada que construímos acima, enquanto a curva verde é baseada na aproximação quarto de volta em que estávamos a trabalhar.
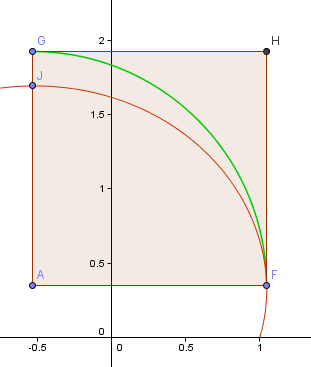
O ponto F é o ponto “mais direito” na espiral, que será o meu ponto de partida para o arco quarto de volta. O ponto J é o ponto mais alto desta porção da espiral.
Ponto A é a intersecção das linhas horizontais e verticais que passam por F e J respectivamente e este será o centro do meu arco.
Agora, o arco GF não está nada perto da porção relacionada da espiral FJ.
Vamos dar mais um passo e ver se a próxima parte é melhor.
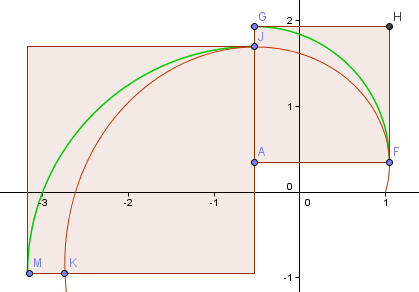
Como pode ver, é pior (como é de esperar, uma vez que nos afastámos mais da origem e o braço em espiral está a ficar maior).
Claramente, isto nunca vai funcionar.
No entanto, na minha anterior Espiral Dourada eu estava usando:
r(t) = e0.30635t
A constante a, tinha valor 1.
Se quisermos que os nossos arcos aproximados sejam um bom ajuste para a Espiral Dourada real, precisamos usar um valor de (provavelmente não surpreendentemente)
a = φ = 1.618103399…
Esta dá-nos as seguintes curvas, semelhantes ao gráfico na Wikipedia.
A curva vermelha é a Espiral Dourada,
r(t) = 1.618013 e0.30635t
A curva verde é a colecção de arcos circulares.
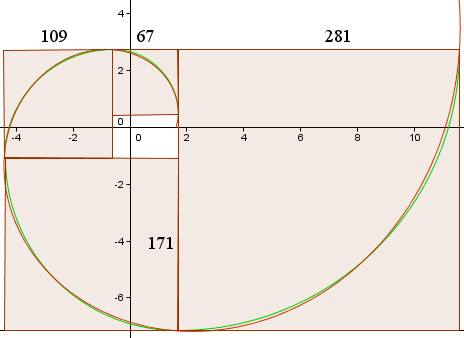
O comprimento lateral dos quadrados (em pixels) é mostrado e podemos ver que estão aproximadamente na proporção 1,618013…
Espiral dourada na mídia
Do Mundo Matemático da Wolfram:
No episódio 4 da temporada “Masterpiece” (2008) do drama criminal “Criminal Minds” da CBS-TV, os agentes da Unidade de Análise Comportamental do FBI são confrontados por um assassino em série que usa a sequência numérica de Fibonacci para determinar o número de vítimas para cada um dos seus episódios de morte. Neste episódio, o personagem Dr. Reid também nota que as localizações dos assassinatos estão no gráfico de uma espiral dourada, e ir para o centro da espiral permite a Reid determinar a localização da base de operações do assassino.
Aqui estão informações mais interessantes do Mathworld da Wolfram:
Espiral Logarítmica
Para os geeks – design usando a Espiral Dourada
É acreditado por muitos que designs usando a Golden Ratio e a Espiral Dourada são agradáveis ao olho.
Even Twitter recentemente redesenhou sua página principal usando a Espiral Dourada.
Aqui está um ótimo artigo de um cara que construiu uma espiral dourada sem imagens. (Principalmente para aqueles interessados em Web design)
Espiral dourada sem imagens – usando CSS e jQuery
Como ele sugere no artigo, a tromba de um elefante também está perto da Espiral Dourada.

Tronco de elefante – quase uma Espiral Dourada
Conclusão
A Espiral Dourada é um tópico interessante – um tópico que vale a pena buscar não só pelos agradáveis desenhos envolvidos, mas também pela interessante matemática por trás deles.
Espero que isso ajude a responder a sua pergunta, Pehr!