Sun, 18 Jun 2006
1+1=2
Whitehead og Russells Principia Mathematica er berømte for at bruge tusind sider på at bevise, at 1+1=2. Selvfølgelig beviser den også en masse andre ting. Hvis de kun havde ønsket at bevise, at 1+1=2, ville det sandsynligvis kun have taget halvt så meget plads.
Principia Mathematica er en mærkelig bog, som er værd at se nærmere på ud fra et historisk synspunkt såvel som et matematisk synspunkt. Den blev skrevet omkring 1910, og den matematiske logik var dengang stadig i sin vorden, frisk fra den transformation, som Peano og Frege havde foretaget af den. Notationen er noget uklar, fordi den matematiske notation har udviklet sig betydeligt siden da. Og mange af de enkle teknikker, som vi i dag tager for givet, er fraværende.Ligesom et dårligt skrevet computerprogram er en stor del af Principia Mathematicas hovedbestanddel gentagelseskode, separate afsnit, der stort set siger de samme ting, fordi forfatterne endnu ikke har lært de teknikker, der ville gøre det muligt at kombinere disse afsnit til ét.
For eksempel begynder afsnit ∗22, “Calculus of Classes”, med at definere undermængderelationen (∗22.01) og operationerne for mængdeunion og mængdeintersektion (∗22.02 og .03), komplementet af en mængde (∗22.04) og forskellen af to mængder (∗22.05). Derefter beviser den kommutativitet og associativitet af mængders sammenslutning og sammensnittet af mængder (∗22.51, .52, .57 og .7), forskellige egenskaber som !!\alpha\cap\alpha = \alpha!! (∗22.5) og lignende, og arbejder sig frem til sætninger som ∗22.92: !!\alpha\subset\beta \rightarrow \alpha\cup(\beta -\alpha)!!!.
Afsnit ∗23 er “Calculus of Relations” og begynder på næsten nøjagtig samme måde med at definere subrelationsrelationen (∗23.01), og operationerne for relationel union og intersektion (∗23.02 og .03), komplementet til en relation (∗23.04) og forskellen af to relationer (∗23.05). Itlater beviser kommutativitet og associativitet af relationel union og intersektion (∗23.51, .52, .57,og .7), forskellige egenskaber som !!\alpha\dot\cap\alpha = \alpha!! (∗22.5) og lignende, og arbejder sig frem til sætninger som ∗23.92: !!\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot-\alpha)!!!.
Det afsnit ∗24 handler om eksistensen af mængder, nulmængden !!\Lambda!!, den universelle mængde !!{\rm V}!!!, deres egenskaber osv., og så er afsnit ∗24 duplikeret i ∗25 i en række sætninger om eksistensen af relationer, nulrelationen !!\dot\Lambda!!, den universelle relation !!\dot {\rm V}!!, deres egenskaber osv.
Det var sådan Whitehead og Russell gjorde det i 1910. Hvordan ville vi gøre det i dag? En relation mellem S og T er defineret som en delmængde afS × T og er derfor en mængde. Union, intersektion, forskel og de andre operationer er præcis de samme for relationer som for mængder, fordi relationer er mængder. Alle sætninger om unioner og krydsninger af relationer, som f.eks.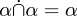 
, forsvinder bare, fordi vi allerede har bevist dem for mængder, og relationer er mængder. Nulrelationen er nulmængden. Den universelle relation er den universelle mængde.
En enorm mængde andet maskineri forsvinder i 2006 på grund af foreningen af relationer og mængder. Principia Mathematica har brug for en særlig notation og en særlig definition af resultatet af at begrænse en relation til de par, hvis første element er et medlem af en bestemt mængde S, eller hvis andet element er et medlem af S, eller hvis begge elementer er medlemmer af S; i 2006 ville vi bare bruge den almindelige mængdeintersektionsoperation og tale om R ∩(S×B) eller hvad ved jeg.
Whitehead og Russell kunne ikke gøre dette i 1910, fordi der manglede en afgørende del af maskineriet: det ordnede par. I 1910 var der ingen, der vidste, hvordan man kunne opbygge et ordnet par ud fra blot logik og mængder. I 2006 (eller endog1956) ville vi definere det ordnede par <a, b> som mængden {{a}, {a, b}}}. Derefter ville vi vise som et teorem, at <a, b> = <c, d>, hvis og kun hvis a=c og b=d, ved hjælp af mængdens egenskaber. Derefter definerer vi A×B som mængden af alle p således, at p = <a,b> ∧ a ∈ A ∧ b∈ B. Derefter definerer vi en relation mellem mængderneA og B som en delmængde af A×B. Så ville vi få alle ∗23 og ∗25 og en masse ∗33 og ∗35 og ∗36 gratis, og sandsynligvis også en masse andre ting.
(I øvrigt blev {{a}, {a, b}}-tingen opfundet af Kuratowski. Det tilskrives normalt Norbert Wiener, menWieners idé var faktisk mere kompliceret, selv om den lignede den.)
Der er ingen ordnede par i Principia Mathematica,undtagen implicit. Der er næsten ikke engang nogen mængder. Whitehead ogRussell ønsker at basere alt på logik. For Whitehead og Russell er det grundlæggende begreb den “propositionelle funktion”, som er en funktion φ, hvis output er en sandhedsværdi. For hver sådan funktion findes der en tilsvarende mængde, som de betegner med !!\hat x\phi(x)!!, dvs. mængden af alle x således, at φ(x) er sand. For Whitehead og Russell er en arelation impliceret af en propositionel funktion af to variabler, analogt med den måde, hvorpå en mængde er impliceret af en propositionel funktion af én variabel. I 2006 undlader vi at bruge “funktioner af to variabler” og taler blot om funktioner, hvis (eneste) argument er et ordnet par; en relation bliver så mængden af alle ordnede par, for hvilke en funktion er sand.
Russell skulle have sagt, at opdagelsen af Shefferstroke (en enkelt logisk operatør, hvorfra alle andre logiske operatører kan bygges) var et enormt fremskridt og ville ændre alting. Det virker mærkeligt for os i dag, for opdagelsen af Sheffer-stregen virker så enkel, og den ændrer ikke rigtig noget vigtigt. Man skal blot tilføje en note i begyndelsen af kapitel 1, der siger, at ∼p og p∨q er forkortelser for henholdsvis p|p og p|p.|.q|q, bevise de fem fundamentale aksiomer og lade alt andet være som før. Men Russell kunne med en vis retfærdighed have sagt det samme om opdagelsen af, at ordnede par kan fortolkes som mængder, en simpel opdagelse, som virkelig ville have forvandlet Principia Mathematica til et helt andet værk.
Men med denne baggrund på plads kan vi diskutere Principia Mathematicas bevis for 1+1=2. Dette forekommer ret sent i Principia Mathematica, i afsnit ∗102. Min forkortede version går kun til ∗56, men det er langt nok til at nå frem til den vigtige forløber-sætning, ∗54.43, som er scannet nedenfor:
Notationen kan være overvældende, så lad os fokusere på sætningen og ignorere alt andet, selv den nyttigebemærkning nederst i teksten:
Dette er den sætning, der bevises; det, der følger, er beviset.
Nu skal jeg forklare notationen, som har ændret sig noget siden1910. For det første bruger Principia Mathematica Peanos “prikker”-notation til at afklare præcedens, hvor vi nu bruger parenteser i stedet. Punktnotationen kræver lidt tilvænning, men har nogle klare fordele i forhold til parenteser. Idéen er blot, at man angiver gruppering ved at sætte prikker ind, således at (1+2)×(3+4)& gange(5+6) skrives som1+2.×.3+4.×.5+6. Den midterste underformel står mellem et par prikker. Underformlen (1+2) er også mellem et par prikker, men prikken i venstre ende er overflødig, og vi udelader den; på samme måde er underformlen (5+6) afgrænset af en prik i venstre side og af slutningen af formlen i højre side.
Hvad sker der, hvis du har brug for at indlejre parenteser? Så bruger du flere prikker. En dobbelt prik (:) er som en enkelt prik, men stærkere. Vi skriver f.eks. ((1+2)×3)+4 som 1+2 . × 3 : + 4, og den dobbelte prik adskiller hele 1+2 . × 3-udtrykket til en enkelt underformel, som +4 gælder for.
Sommetider har man brug for flere præcedensniveauer, og så bruger man triplet prik (.: og :.) og firdobbelt (::). Denne formel har, som du kan se, dobbelte og tredobbelte prikker. Hvis vi omsætter prikkerne til standardparenteser, får vi $$$\ast54,43. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2))))$$$. Dette ser noget mere uoverskueligt ud end versionen med prikker, og i ukomplicerede formler kan man have problemer med at finde ud af, hvilke parenteser der passer til hvilke. Med prikkerne er det altid nemt. Så jeg synes, det er lidt uheldigt, at denne konvention er gået ud af brug.
Symbolet !!\vdash!! er uændret; det betyder, at den formel, som det gælder for, påstås at være sand. !!\supset!! er logisk implikation, og !!\equiv!! er logisk ækvivalens. Λ er den tomme mængde, som vi i dag skriver ∅. ∩ ∪ og ∈ har deres modernebetydninger: ∩ og ∪ er mængdesnittet og unionoperatorerne, og x∈y betyder, at x er et element i mængden y.
De resterende punkter er semantiske. α og β er mængder. 1betegner mængden af alle mængder, der har præcis ét element. Det vil sige,det er mængden { c : der findes en sådan a, at c = {a } }. Sætninger om 1 omfatter f.eks.:
- at Λ∉1 (∗52.21),
- at hvis α∈1 så er der en x sådan at α ={x} (∗52.1), og
- at {x}∈1 (∗52.22).
2 er på samme måde mængden af alle mængder, der har præcis to elementer. En vigtig sætning om 2 er ∗54.3, som siger $$$\ast54.3. \vdash 2 = \hat\alpha\{ (\existerer x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\i 1 \}.$$$I Principia Mathematica notation skrives {x}, mængden, der indeholder x og intet andet, som ι’x, så denne sætning siger, at 2 er identisk med mængden af alle α, således atα har et element x , som, når det fjernes fra α, efterlader en mængde med 1 element.
Så her er sætning ∗54.43 igen:
Det hævder, at hvis mængderne α og β hver har præcis ét element, så er de disjoint (dvs. de har ingen elementer til fælles), hvis og kun hvis deres union har præcis to elementer.
Beviset, som vises i scanningen ovenfor efter ordet “Dem.” (forkortelse for “demonstration”) lyder således:
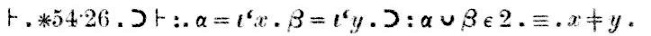
“Sætning ∗54.26implicerer, at hvis α = {x} og β = {y}, såα∪β har 2 elementer, hvis og kun hvis x erforskellig fra y.”
“Ifølge sætning ∗51.231 er denne sidste del (x er forskellig fray) sandt, hvis og kun hvis {x} og {y} erdisjoint.”
“Ifølge ∗13.12 er denne sidste bit ({x} og {y} er disjoint) sandt, hvis og kun hvis α og β selv er disjoint.” Den delvise konklusion på dette punkt,som er mærket (1), er, at hvis α = {x} og β ={y}, så er α∪β ∈ 2 hvis og kun hvisα∩β = Λ.
Beviset fortsætter: “Konklusion (1), med sætningerne ∗11.11 og ∗11.35,indebærer, at hvis der findes x og y, således at α er{x} og β er {y}, så α∪β ∈ 2hvis og kun hvis α og β er disjunkte.” Denne konklusion er mærket med (2).
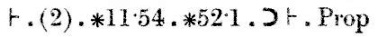
Slutteligt indebærer konklusion (2), sammen med sætningerne ∗11.54 og ∗52.1,den sætning, som vi forsøgte at bevise.
Måske er det, man skal lægge mærke til her, hvor meget små trinene er. ∗54.26, som denne sætning er stærkt afhængig af, er næsten den samme; den hævder, at {x}∪{y} ∈ 2, hvis og kun hvis x≠y. ∗54.26 afhænger igen af ∗54.101, som siger, at α har 2 elementer, hvis og kun hvis der findes x ogy, der ikke er ens, således at α = {x} ∪{y}. ∗54.101 er bare en lille smule forskellig fra definitionen af 2. Sætning ∗51.231 siger, at {x} og {y} er disjoint hvis og kun hvis x og y er forskellige.∗52.1 er en grundlæggende egenskab af 1; vi har set den før.
De andre sætninger, der citeres i demonstrationen, er meget små tekniske spørgsmål. ∗11.54 siger, at man kan tage en påstand om, at to ting eksisterer, og adskille den i to påstande, der hver især påstår, at den ene af tingene eksisterer. ∗11.11 er endnu slankere: den siger, at hvis φ(x, y) altid er sandt, så kan man vedhæfte en universel kvantifikator og hævde, at φ(x, y) er sandt for alle x og y. ∗13.12 drejer sig om substitution af ligemænd for ligemænd: hvis x og y er ens, så besidder x en egenskab ψ hvis og kun hvis y også gør det.
Jeg har ikke set de senere dele af Principia Mathematica, fordi mit eksemplar stopper efter afsnit ∗56, og de aritmetiske ting er meget senere. Men denne sætning har tydeligvis betydningen af 1+1=2 i sig, og den senere sætning (∗110.643)der faktisk hævder 1+1=2 afhænger stærkt af denne sætning.
Men selv om jeg ikke er helt sikker på, hvad der kommer til at ske senere (jeg har allerede spildt alt for meget tid på dette til at bruge mere tid på at få den fulde version fra biblioteket), kan jeg lave et kvalificeret gæt. Principia Mathematica vil definere tallet 17 som værende mængden af alle 17-elementers mængder, og det samme gælder for alle andre tal; brugen af symbolet 2 til at repræsentere mængden af alle 2-elementers mængder er et tegn på dette. Disse sæt af alle sæt af en vis størrelse vil derefter blive identificeret som “kardinaltallene”.
Principia Mathematica vil definere summen af kardinaltallene p og q på følgende måde: man tager en repræsentativ mængde fra p; a har p elementer. Tag et repræsentativt sæt bfra q; b har q elementer. Lad c =a∪b. Hvis c er en del af et kardinaltal r, og hvis a og b er adskilte, er summen af p og q lig med r.
Med denne definition kan man bevise de sædvanlige ønskelige egenskaber ved addition, f.eks. x + 0 = x, x + y = y + x og 1 + 1 = 2.
I særdeleshed følger 1+1=2 direkte af sætning ∗54.43; det er lige hvad vi ønsker, for for for at beregne 1+1 skal vi finde to usammenhængende repræsentanter for 1 og tage deres forening; ∗54.43 hævder, at foreningen skal være et element af 2, uanset hvilke repræsentanter vi vælger, så 1+1=2.
Post scriptum: Peter Norvig siger, at omskrivningen iPrincipia Mathematica-notationen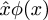 
er den ultimative kilde til brugen af ordetlambda til at betegne en anonym funktion i programmeringssprogene Lisp og Python. Jeg er sikker på, at du ved, at disse sprog har fået “lambda” fra Alonzo Churchs brug af det græske bogstav λ til at repræsentere funktionsabstraktion i sin “λ-kalkule”: I Lisp er(lambda (u) B) en funktion, der tager et argumentu og returnerer værdien af B; i λ-kalkulen er λu.B en funktion, der tager et argumentu og returnerer værdien af B. Norvig siger, at Church oprindeligt havde planlagt at skrive funktionenλu.B som û.B, men at hans printer ikke kunne lave omvendte accenter. Så han overvejede at flyttecirkumflexen til venstre og bruge et stort lambda i stedet:Λu.B. Det store Λ lignede for megetelogisk og ∧, hvilket var forvirrende, så han brugte i stedet lille lambdaλ.
Post post scriptum: Alle siger altid “Russell og Whitehead”.Google-resultaterne for “Russell og Whitehead” overgår f.eks. dem for “Whitehead og Russell” med to til en. Hvorfor? På omslaget og på titelbladet står der “Alfred North Whitehead og Bertrand Russell,F.R.S.”. Hvordan og hvornår har Whitehead mistet sin førsteplads?
permanent link