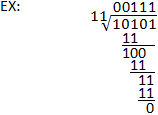Utiliza las siguientes calculadoras para realizar la suma, la resta, la multiplicación o la división de dos valores binarios, así como para convertir valores binarios en valores decimales, y viceversa.

Cálculo binario-Sumar, restar, multiplicar, o Dividir
Convertir Valor Binario a Valor Decimal
Convertir Valor Decimal a Valor Binario
Calculadora Hexadecimal Relacionada | Calculadora de Subredes IP
El sistema binario es un sistema numérico que funciona virtualmente idéntico al sistema numérico decimal con el que la gente está probablemente más familiarizada. Mientras que el sistema numérico decimal utiliza el número 10 como base, el sistema binario utiliza el 2. Además, aunque el sistema decimal utiliza los dígitos del 0 al 9, el sistema binario sólo utiliza el 0 y el 1, y cada dígito se denomina bit. Aparte de estas diferencias, las operaciones como la suma, la resta, la multiplicación y la división se calculan siguiendo las mismas reglas que en el sistema decimal.
Casi toda la tecnología y los ordenadores modernos utilizan el sistema binario debido a su facilidad de implementación en los circuitos digitales utilizando puertas lógicas. Es mucho más sencillo diseñar hardware que sólo necesita detectar dos estados, encendido y apagado (o verdadero/falso, presente/ausente, etc.). Utilizar un sistema decimal requeriría un hardware que pudiera detectar 10 estados para los dígitos del 0 al 9, y es más complicado.
A continuación se muestran algunas conversiones típicas entre valores binarios y decimales:
Conversión Binaria/Decimal
| Decimal | Binario |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Aunque trabajar con el binario puede parecer inicialmente confuso, entender que cada valor de lugar binario representa 2n, al igual que cada lugar decimal representa 10n, debería ayudar a clarificar. Tomemos como ejemplo el número 8. En el sistema numérico decimal, el 8 se sitúa en el primer lugar decimal a la izquierda del punto decimal, lo que significa el lugar 100. Esencialmente esto significa:
8 × 100 = 8 × 1 = 8
Usando el número 18 para comparar:
(1 × 101) + (8 × 100) = 10 + 8 = 18
En binario, el 8 se representa como 1000. Leyendo de derecha a izquierda, el primer 0 representa el 20, el segundo el 21, el tercero el 22 y el cuarto el 23; igual que en el sistema decimal, pero con una base de 2 en lugar de 10. Como 23 = 8, se introduce un 1 en su posición y se obtiene 1000. Usando 18, o 10010 como ejemplo:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
El proceso paso a paso para convertir del sistema decimal al binario es:
- Encuentra la mayor potencia de 2 que esté dentro del número dado
- Resta ese valor al número dado
- Encuentra la mayor potencia de 2 dentro del resto encontrado en el paso 2
- Repite hasta que no haya resto
- Introduce un 1 por cada valor de lugar binario que se haya encontrado, y un 0 para el resto
Usando el objetivo de 18 de nuevo como un ejemplo, a continuación es otra manera de visualizar esto:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instancias dentro de 18 | 1 | 0 | 0 | 1 | 0 |
| Objetivo: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
La conversión del sistema binario al decimal es más sencilla. Determina todos los valores de lugar donde ocurre el 1, y encuentra la suma de los valores.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Entonces: 16 + 4 + 2 + 1 = 23.
Suma binaria
La suma binaria sigue las mismas reglas que la suma en el sistema decimal, excepto que en lugar de arrastrar un 1 cuando los valores sumados son iguales a 10, el arrastre se produce cuando el resultado de la suma es igual a 2. Consulte el ejemplo siguiente para obtener una aclaración.
Note que en el sistema binario:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, el arrastre del 1, es decir 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
La única diferencia real entre la suma binaria y la decimal es que el valor 2 en el sistema binario es el equivalente al 10 en el sistema decimal. Observa que los 1 en superíndice representan dígitos que se arrastran. Un error común que hay que tener en cuenta al realizar una suma binaria es el caso en el que 1 + 1 = 0 también tiene un 1 arrastrado de la columna anterior a su derecha. El valor en la parte inferior debería ser el 1 del 1 arrastrado en lugar del 0. Esto se puede observar en la tercera columna desde la derecha en el ejemplo anterior.
Resta binaria
De forma similar a la suma binaria, hay pocas diferencias entre la resta binaria y la decimal, excepto las que surgen de utilizar sólo los dígitos 0 y 1. El préstamo se produce en cualquier caso en el que el número que se resta es mayor que el número del que se resta. En la resta binaria, el único caso en el que es necesario tomar prestado es cuando se resta 1 de 0. Cuando esto ocurre, el 0 de la columna que toma prestado se convierte esencialmente en «2» (cambiando el 0-1 en 2-1 = 1) mientras que se reduce el 1 de la columna de la que se toma prestado en 1. Si la columna siguiente también es 0, habrá que tomar prestado de cada columna subsiguiente hasta que una columna con un valor de 1 pueda reducirse a 0. Consulte el ejemplo siguiente para aclararlo.
Note que en el sistema binario:
- 0 – 0 = 0
0 – 1 = 1, se toma prestado 1, resultando -1 arrastrado
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Nótese que los superíndices mostrados son los cambios que se producen en cada bit al tomar prestado. La columna que se toma prestada obtiene esencialmente 2 al tomarla prestada, y la columna de la que se toma prestada se reduce en 1.
Multiplicación binaria
La multiplicación binaria es posiblemente más sencilla que su homóloga decimal. Dado que los únicos valores utilizados son 0 y 1, los resultados que deben sumarse son o bien el mismo que el primer término, o bien 0. Obsérvese que en cada fila posterior hay que añadir 0 de marcador de posición, y el valor se desplaza hacia la izquierda, al igual que en la multiplicación decimal. La complejidad en la multiplicación binaria surge de la tediosa adición binaria que depende de cuántos bits hay en cada término. Refiérase al ejemplo de abajo para aclararlo.
Note que en el sistema binario:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Como puede verse en el ejemplo anterior, el proceso de multiplicación binaria es el mismo que el de la multiplicación decimal. Observe que el marcador de posición 0 está escrito en la segunda línea. Normalmente el marcador de posición 0 no está presente visualmente en la multiplicación decimal. Aunque se puede hacer lo mismo en este ejemplo (con el marcador de posición 0 asumido en lugar de explícito), se incluye en este ejemplo porque el 0 es relevante para cualquier calculadora de suma/resta binaria, como la que se proporciona en esta página. Si no se mostrara el 0, sería posible cometer el error de excluir el 0 al sumar los valores binarios mostrados arriba. Observe de nuevo que en el sistema binario, cualquier 0 a la derecha de un 1 es relevante, mientras que cualquier 0 a la izquierda del último 1 del valor no lo es.
EX:
- 1 0 1 0 1 0 0
= 0 0 1 0 1 0 1 0 0
≠ 1 0 1 0 0 0
División binaria
El proceso de división binaria es similar a la división larga en el sistema decimal. El dividendo se sigue dividiendo por el divisor de la misma manera, con la única diferencia significativa del uso de la resta binaria en lugar de la decimal. Tenga en cuenta que una buena comprensión de la resta binaria es importante para llevar a cabo la división binaria. Consulte el ejemplo siguiente, así como la sección de sustracción binaria para aclararlo.