La presión indica la fuerza normal por unidad de superficie en un punto dado que actúa sobre un plano determinado. Dado que en un fluido en reposo no hay tensiones de cizallamiento – la presión en un fluido es independiente de la dirección.
Para los fluidos -líquidos o gases- en reposo el gradiente de presión en la dirección vertical depende sólo del peso específico del fluido.
Cómo cambia la presión con la elevación en un fluido puede expresarse como
Δp = – γ Δh (1)
donde
Δp = cambio de presión (Pa, psi)
Δh = cambio en la altura (m, in)
γ = peso específico del fluido (N/m3, lb/ft3)
El gradiente de presión en dirección vertical es negativo – la presión disminuye hacia arriba.
Peso específico
El peso específico de un fluido puede expresarse como:
γ = ρ g (2)
donde
ρ = densidad del fluido (kg/m3, slugs/ft3)
g = aceleración de la gravedad (9.81 m/s2, 32,174 pies/s2)
En general, el peso específico – γ – es constante para los fluidos. Para los gases el peso específico – γ – varía con la elevación (y la compresión).
La presión ejercida por un fluido estático depende sólo de
- la profundidad del fluido
- la densidad del fluido
- la aceleración de la gravedad
Presión estática en un fluido
Para un fluido incompresible -como un líquido- la diferencia de presión entre dos elevaciones puede expresarse como:
Δp = p2 – p1
= – γ (h2 – h1) (3)
donde
p2 = presión en el nivel 2 (Pa, psi)
p1 = presión en el nivel 1 (Pa, psi)
h2 = nivel 2 (m, ft)
h1 = nivel 1 (m, ft)
(3) puede transformarse en:
Δp = p1 – p2
= γ (h2 – h1) (4)
o
p1 – p2 = γ Δh (5)
donde
Δh = h2 – h1 = diferencia de elevación – el dept hacia abajo desde la ubicación h2 a h1 (m, ft)
o
p1 = γ Δh + p2 (6)
Ejemplo – Presión en un fluido
La presión absoluta a la profundidad del agua de 10 m se puede calcular como:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 o Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
donde
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = presión a nivel de superficie = presión atmosférica = 101,3 kPa
La presión manométrica puede calcularse estableciendo p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
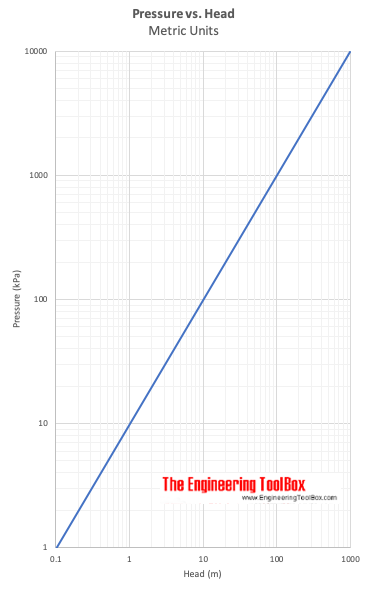
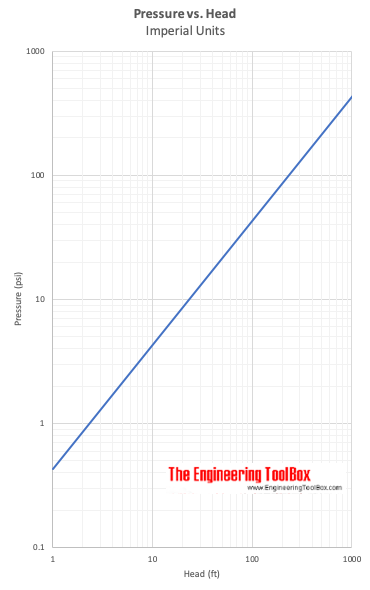
Presión vs. Cabeza
(6) puede transformarse en:
Δh = (p2 – p1) / γ (7)
Δh expresa la cabeza – la diferencia de altura de una columna de fluido de peso específico – γ – necesaria para dar una diferencia de presión Δp = p2 – p1.
Ejemplo – Presión vs. Altura
Una diferencia de presión de 5 psi (lbf/in2) equivale a la altura en el agua
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11,6 pies de agua
o cabeza en Mercurio
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0,85 pies de mercurio
El peso específico del agua es 62.4 (lb/ft3) y el peso específico del mercurio es de 847 (lb/ft3).
- Velocidad – Presión Dinámica vs. Altura