Utilisez les calculatrices suivantes pour effectuer l’addition, la soustraction, la multiplication ou la division de deux valeurs binaires, ainsi que pour convertir des valeurs binaires en valeurs décimales, et vice versa.

Calcul binaire-Ajouter, soustraire, multiplier, ou diviser
Convertir une valeur binaire en valeur décimale
Convertir une valeur décimale en valeur binaire
Calculatrice hexadécimale connexe | Calculatrice de sous-réseau IP
Le système binaire est un système numérique qui fonctionne de manière pratiquement identique au système numérique décimal avec lequel les gens sont probablement plus familiers. Alors que le système numérique décimal utilise le nombre 10 comme base, le système binaire utilise 2. En outre, bien que le système décimal utilise les chiffres 0 à 9, le système binaire n’utilise que 0 et 1, et chaque chiffre est appelé un bit. Hormis ces différences, les opérations telles que l’addition, la soustraction, la multiplication et la division sont toutes calculées selon les mêmes règles que le système décimal.
Presque toute la technologie moderne et les ordinateurs utilisent le système binaire en raison de sa facilité de mise en œuvre dans les circuits numériques utilisant des portes logiques. Il est beaucoup plus simple de concevoir un matériel qui ne doit détecter que deux états, marche et arrêt (ou vrai/faux, présent/absent, etc.). L’utilisation d’un système décimal nécessiterait un matériel capable de détecter 10 états pour les chiffres de 0 à 9, ce qui est plus compliqué.
Voici quelques conversions typiques entre les valeurs binaires et décimales :
Conversion binaire/décimal
| Décimal | Binaire |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Bien que travailler avec le binaire puisse initialement sembler déroutant, comprendre que chaque valeur de place binaire représente 2n, tout comme chaque place décimale représente 10n, devrait aider à clarifier. Prenons l’exemple du nombre 8. Dans le système numérique décimal, 8 est positionné à la première place décimale à gauche de la virgule, signifiant la place 100. Cela signifie essentiellement :
8 × 100 = 8 × 1 = 8
En utilisant le nombre 18 pour la comparaison :
(1 × 101) + (8 × 100) = 10 + 8 = 18
En binaire, 8 est représenté par 1000. En lisant de droite à gauche, le premier 0 représente 20, le deuxième 21, le troisième 22 et le quatrième 23 ; tout comme le système décimal, sauf que la base est 2 plutôt que 10. Comme 23 = 8, un 1 est entré à sa place, ce qui donne 1000. En utilisant 18, ou 10010 comme exemple:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Le processus étape par étape pour convertir du système décimal au système binaire est :
- Trouver la plus grande puissance de 2 qui se trouve dans le nombre donné
- Soustraire cette valeur du nombre donné
- Trouver la plus grande puissance de 2 dans le reste trouvé à l’étape 2
- Répéter jusqu’à ce qu’il n’y ait plus de reste
- Entrer un 1 pour chaque valeur de place binaire qui a été trouvée, et un 0 pour le reste
En utilisant à nouveau la cible de 18 comme exemple, voici une autre façon de visualiser cela :
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instances dans 18 | 1 | 0 | 0 | 1 | 0 |
| Cible : 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
La conversion du système binaire au système décimal est plus simple. Déterminez toutes les valeurs de place où 1 apparaît, et trouvez la somme des valeurs.
EX : 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Hence : 16 + 4 + 2 + 1 = 23.
Addition binaire
L’addition binaire suit les mêmes règles que l’addition dans le système décimal, sauf qu’au lieu de reporter un 1 lorsque les valeurs ajoutées sont égales à 10, le report a lieu lorsque le résultat de l’addition est égal à 2. Reportez-vous à l’exemple ci-dessous pour plus de précisions.
Notez que dans le système binaire :
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, le report du 1, soit . 10
EX :
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
La seule différence réelle entre l’addition binaire et décimale est que la valeur 2 dans le système binaire est l’équivalent de 10 dans le système décimal. Notez que les 1 en exposant représentent les chiffres qui sont reportés. Une erreur courante à laquelle il faut faire attention lorsqu’on effectue une addition binaire est le cas où 1 + 1 = 0 a également un 1 reporté de la colonne précédente à sa droite. La valeur en bas devrait alors être 1 à partir du 1 reporté plutôt que 0. Cela peut être observé dans la troisième colonne à partir de la droite dans l’exemple ci-dessus.
Soustraction binaire
De même que l’addition binaire, il y a peu de différences entre la soustraction binaire et décimale, sauf celles qui découlent de l’utilisation des seuls chiffres 0 et 1. L’emprunt se produit dans tous les cas où le nombre qui est soustrait est plus grand que le nombre dont il est soustrait. Dans la soustraction binaire, le seul cas où l’emprunt est nécessaire est lorsque 1 est soustrait de 0. Lorsque cela se produit, le 0 dans la colonne d’emprunt devient essentiellement « 2 » (changeant le 0-1 en 2-1 = 1) tout en réduisant le 1 dans la colonne qui est empruntée de 1. Si la colonne suivante est également 0, l’emprunt devra se produire à partir de chaque colonne suivante jusqu’à ce qu’une colonne avec une valeur de 1 puisse être réduite à 0. Se référer à l’exemple ci-dessous pour clarification.
Notez que dans le système binaire :
- 0 – 0 = 0
0 – 1 = 1, emprunt de 1, ce qui entraîne un report de -1
1 – 0 = 1
1 – 1 = 0
EX1 :
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2 :
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Notez que les exposants affichés sont les changements qui se produisent sur chaque bit lors de l’emprunt. La colonne emprunteuse obtient essentiellement 2 de l’emprunt, et la colonne qui est empruntée est réduite de 1.
Multiplication binaire
La multiplication binaire est sans doute plus simple que sa contrepartie décimale. Puisque les seules valeurs utilisées sont 0 et 1, les résultats qui doivent être ajoutés sont soit les mêmes que le premier terme, soit 0. Notez que dans chaque ligne suivante, des 0 placeholder doivent être ajoutés, et la valeur décalée vers la gauche, tout comme dans la multiplication décimale. La complexité de la multiplication binaire provient de l’addition binaire fastidieuse qui dépend du nombre de bits de chaque terme. Reportez-vous à l’exemple ci-dessous pour plus de clarté.
Notez que dans le système binaire :
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX :
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Comme on peut le voir dans l’exemple ci-dessus, le processus de la multiplication binaire est le même que celui de la multiplication décimale. Notez que le caractère de remplacement 0 est écrit dans la deuxième ligne. En général, le caractère de remplacement 0 n’est pas présent visuellement dans la multiplication décimale. Bien qu’il soit possible de faire la même chose dans cet exemple (le caractère de remplissage 0 étant supposé plutôt qu’explicite), il est inclus dans cet exemple parce que le 0 est pertinent pour toute calculatrice d’addition/soustraction binaire, comme celle fournie sur cette page. Sans l’affichage du 0, il serait possible de faire l’erreur d’exclure le 0 lors de l’addition des valeurs binaires affichées ci-dessus. Notez à nouveau que dans le système binaire, tout 0 à droite d’un 1 est pertinent, tandis que tout 0 à gauche du dernier 1 de la valeur ne l’est pas.
EX:
- 1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 1 0 0 0
Division binaire
Le processus de division binaire est similaire à la division longue dans le système décimal. Le dividende est toujours divisé par le diviseur de la même manière, la seule différence significative étant l’utilisation de la soustraction binaire plutôt que décimale. Notez qu’une bonne compréhension de la soustraction binaire est importante pour effectuer une division binaire. Reportez-vous à l’exemple ci-dessous, ainsi qu’à la section sur la soustraction binaire pour obtenir des précisions.
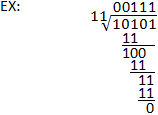
.