La pression indique la force normale par unité de surface en un point donné agissant sur un plan donné. Comme il n’y a pas de contraintes de cisaillement présentes dans un fluide au repos – la pression dans un fluide est indépendante de la direction.
Pour les fluides – liquides ou gaz – au repos, le gradient de pression dans la direction verticale ne dépend que du poids spécifique du fluide.
Comment la pression change avec l’élévation dans un fluide peut être exprimée comme
Δp = – γ Δh (1)
où
Δp = changement de pression (Pa, psi)
Δh = changement de hauteur (m, in)
γ = poids spécifique du fluide (N/m3, lb/ft3)
Le gradient de pression dans la direction verticale est négatif – la pression diminue vers le haut.
Poids spécifique
Le poids spécifique d’un fluide peut être exprimé comme suit :
γ = ρ g (2)
où
ρ = densité du fluide (kg/m3, limaces/pied3)
g = accélération de la gravité (9.81 m/s2, 32,174 ft/s2)
En général, le poids spécifique – γ – est constant pour les fluides. Pour les gaz, le poids spécifique – γ – varie avec l’élévation (et la compression).
La pression exercée par un fluide statique dépend uniquement
- de la profondeur du fluide
- de la densité du fluide
- de l’accélération de la pesanteur
Pression statique dans un fluide
Pour un fluide incompressible – comme un liquide – la différence de pression entre deux élévations peut être exprimée comme :
Δp = p2 – p1
= – γ (h2 – h1) (3)
où
p2 = pression au niveau 2 (Pa, psi)
p1 = pression au niveau 1 (Pa, psi)
h2 = niveau 2 (m, ft)
h1 = niveau 1 (m, ft)
(3) peut être transformé en :
Δp = p1 – p2
= γ (h2 – h1) (4)
ou
p1 – p2 = γ Δh (5)
où
Δh = h2 – h1 = différence d’élévation – la dépt vers le bas de l’emplacement h2 à h1 (m, ft)
ou
p1 = γ Δh + p2 (6)
Exemple – Pression dans un fluide
La pression absolue à une profondeur d’eau de 10 m peut être calculée comme suit :
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 ou Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
où
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = pression au niveau de la surface = pression atmosphérique = 101,3 kPa
La pression manométrique peut être calculée en fixant p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
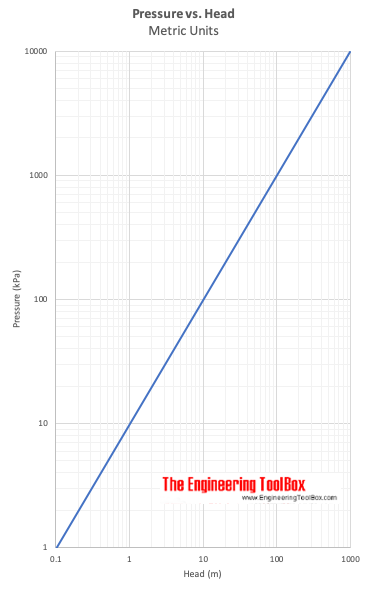
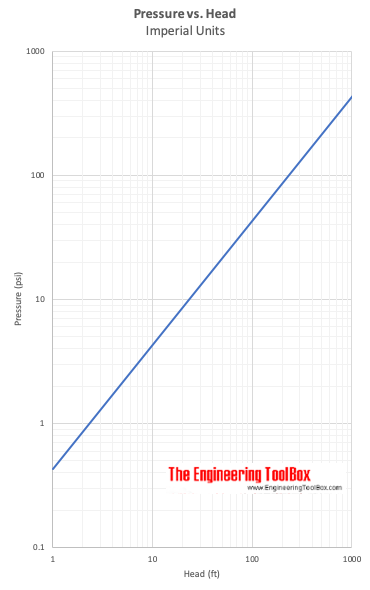
Pression vs. Tête
(6) peut être transformé en :
Δh = (p2 – p1) / γ (7)
Δh exprime la tête – la différence de hauteur d’une colonne de fluide de poids spécifique – γ – nécessaire pour donner une différence de pression Δp = p2 – p1.
Exemple – Pression par rapport à la hauteur de chute
Une différence de pression de 5 psi (lbf/in2) équivaut à une hauteur de chute dans l’eau
(5 lbf/in2) (12 po/pi) (12 po/pi) / (62.4 lb/pi3)
= 11,6 pi d’eau
ou à la tête dans le mercure
(5 lbf/in2) (12 po/pi) (12 po/pi) / (847 lb/pi3)
= 0,85 pi de mercure
Le poids spécifique de l’eau est de 62.4 (lb/ft3) et le poids spécifique du mercure est de 847 (lb/ft3).
- Vélocité – Pression dynamique en fonction de la hauteur
.