
Fern
Ecco una domanda recente del lettore Pehr in Svezia:
Ciao,
Prima di tutto, sito meraviglioso. Lo adoro.
Ho studiato la sezione delle coordinate polari sperando di espandere le mie conoscenze sulla spirale equiangolare. Gli strumenti interattivi sono fantastici, anche se sto avendo difficoltà a ricavare la soluzione matematica esatta del perché la funzione risultante per la spirale aurea è
r = ae^(b(theta))
Per un po’ di background sulla domanda di Pehr, vedi:
Coordinate polari, curve in coordinate polari e spirale equilatera
Le spirali sono comuni in natura e hanno ispirato i matematici per secoli.

Spirale Aloe

Galassia a spirale NGC 5194
Spirali logaritmiche
La spirale aurea di cui Pehr chiede informazioni è un caso speciale della spirale logaritmica.
Le spirali logaritmiche crescono in modo tale che l’angolo di una linea dal centro della spirale alla tangente alla curva in quel punto è costante. Questo è il motivo per cui sono anche conosciute come spirali “equi-angolari”.
Per vedere cosa significa, i 3 angoli acuti segnati nella seguente immagine della felce sono circa 80°

Ferna equi-angolare
Noi normalmente usiamo funzioni in coordinate polari quando descriviamo spirali. Altrimenti, se usiamo coordinate rettangolari ordinarie, le formule diventano molto complesse.
La formula per una spirale logaritmica usando le coordinate polari è:
r = aeθ cot b
dove
r è la distanza dall’origine (o “polo”)
a è una costante
θ è l’angolo (in radianti) dall’asse orizzontale. Quindi le coordinate di un punto sulla curva in coordinate polari è dato da (r, θ).
b è l’angolo (in radianti – l’angolo “uguale”) che la linea dal centro della spirale fa con la tangente alla spirale. Nel caso della felce di cui sopra, b ≈ 1,4 radianti (≈ 80°).
Come conseguenza del modo in cui abbiamo definito la spirale logaritmica, il rapporto delle distanze dal centro a ciascun braccio della spirale di una coppia adiacente è costante.

Bracci della spirale a rapporto costante
Il rapporto
distanza al primo braccio: distanza al secondo braccio
= 29:69
≈ 0.42
L’altro rapporto
distanza dal secondo braccio: distanza dal terzo braccio
= 69:154
≈ 0,45
Vediamo che i rapporti sono quasi uguali. (In una vera spirale logaritmica, sono esattamente gli stessi. La scelta del punto di partenza della felce non è una scienza esatta!)
Spirale aurea
La spirale aurea è un caso speciale della spirale logaritmica.
Possiamo scrivere la spirale logaritmica generale come una funzione in coordinate polari usando t come segue:
r(t) = aet cot b
Nota: Normalmente, usiamo θ per la variabile indipendente, ma spesso usiamo t perché possiamo pensare che la spirale sia tracciata nel tempo. Inoltre, è più facile da scrivere!
La spirale aurea ha la proprietà speciale per cui per ogni 1/4 di giro (90° o π/2 in radianti), la distanza dal centro della spirale aumenta del rapporto aureo φ = 1,6180.
Perché questo avvenga, cot b deve assumere il valore (che viene dalla risoluzione della nostra funzione):
![]()
Utilizzando questo valore, e prendendo il caso semplice in cui a = 1, la nostra funzione diventa:
r(t) = e0.30635t
Da qui in poi useremo l’eccellente strumento grafico gratuito GeoGebra.
Impostazione della spirale aurea con GeoGebra
Ora, se tracciamo la nostra funzione sugli assi delle coordinate ordinarie rettangolari in GeoGebra, otteniamo la seguente curva esponenziale. Si noti che r aumenta sempre di più (diventa più ripida) all’aumentare di t.
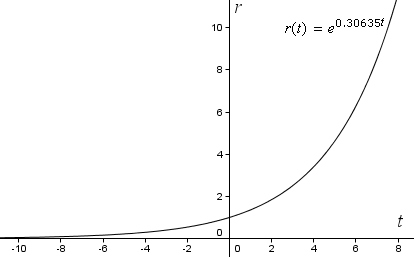
Ma per vedere una spirale, dobbiamo tracciare la curva utilizzando le coordinate polari.
Per convertire la forma polare (che abbiamo) in forma rettangolare (che ci serve per il grafico) in Geogebra, dobbiamo impostare e tracciare la seguente funzione:
a(t) = (r(t) cos(t), r(t) sin(t))
Sostituiamo alcuni valori importanti per vedere cosa significa questa espressione. Partendo da t = 0, otteniamo il punto di partenza della curva:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Quindi significa che partiamo a 1 unità dall’origine lungo l’asse x positivo. Potete vedere il punto di partenza nel seguente grafico della spirale.
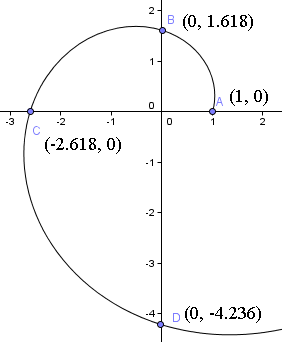
In seguito, ruotiamo di un quarto di giro e troviamo a t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Nota che ora siamo a 1,618 unità dall’origine sull’asse y. Cioè, φ = 1,6180 volte la distanza da cui siamo partiti.
Un’altra rotazione di un quarto di giro ci porta a t = π, dove:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Ora siamo a 2,618 unità di distanza dall’origine lungo l’asse x negativo, o φ = 1,6180 volte la distanza dall’origine che eravamo all’ultimo quarto di giro.
Nota:
φ2 = 2,6180
Possiamo calcolare la nostra prossima posizione, lungo l’asse y negativo, moltiplicando semplicemente quest’ultimo valore per φ = 1,6180, dandoci:
φ3 = 4,23606…
Così la spirale taglierà l’asse y a (0, -4.236).
Un altro quarto di giro ci porterà a φ4 = 6.85410… unità lungo l’asse y positivo, cioè (6.854, 0).
Possiamo vedere che questi valori sono corretti sul nostro grafico a spirale sopra.
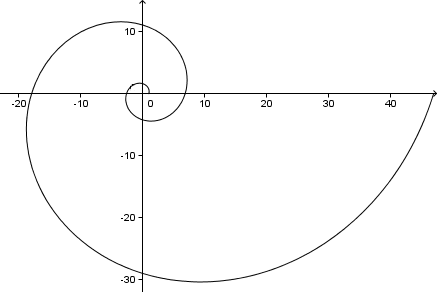
Se continuiamo, otterremo una spirale come la seguente (si tratta di 2 giri completi, o 4π = 720°):
A parte, poiché in questo problema
cot b = 0.30635
allora
b = arccot 0.30635 = 1.274 radianti o circa 73°
Questo è l’angolo che i nostri bracci della spirale fanno con una linea dal centro della spirale. Puoi vedere nel grafico qui sopra che ogni braccio della spirale fa un angolo di 73° con l’asse x (e l’asse y, o qualsiasi linea dal centro).
Approssimazione della Spirale Aurea usando archi di cerchio
Possiamo ottenere una spirale che sembra abbastanza simile alla Spirale Aurea usando archi di cerchio che aumentano in dimensione per il Rapporto Aureo, come segue.
Partiamo con un quadrato 1×1 e disegniamo un arco, centro C, attraverso 2 angoli tali che i lati del quadrato siano tangenti all’arco (cioè, si toccano una sola volta).
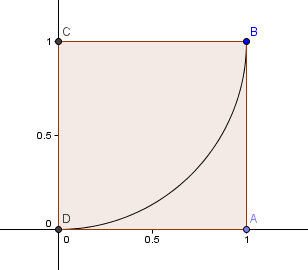
Poi, mettiamo un quadrato con lato di lunghezza φ = 1.6180 sopra il nostro primo quadrato e costruiamo un altro arco circolare, centro E, come prima:
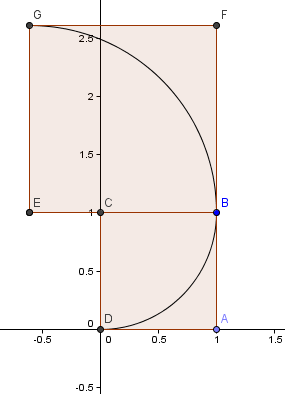
Il nostro prossimo quadrato va a sinistra e ha lati φ2 = 2,6180 = 1 + φ.
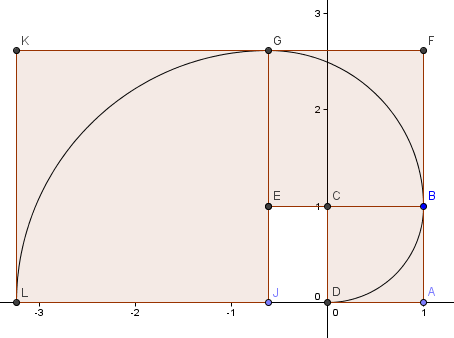
Continuiamo lo schema (abbiamo fatto un altro giro completo) e otteniamo una spirale che assomiglia molto alla nostra Spirale Aurea di prima.
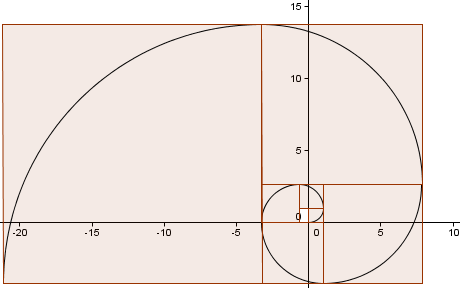
Quanto è vicina la nostra approssimazione?
Ecco l’immagine:
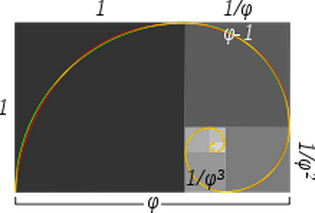
La didascalia dell’immagine afferma:
Spirali d’oro approssimate e vere: la spirale verde è fatta da quarti di cerchio tangenti all’interno di ogni quadrato, mentre la spirale rossa è una spirale aurea, un tipo speciale di spirale logaritmica. Le porzioni sovrapposte appaiono gialle. La lunghezza del lato di un quadrato più grande al successivo quadrato più piccolo è nel rapporto aureo.
Possiamo ricrearlo?
Nell’immagine qui sotto, la curva rossa è la prima parte della spirale aurea che abbiamo costruito sopra, mentre la curva verde è basata sull’approssimazione del quarto di giro su cui stavamo lavorando.
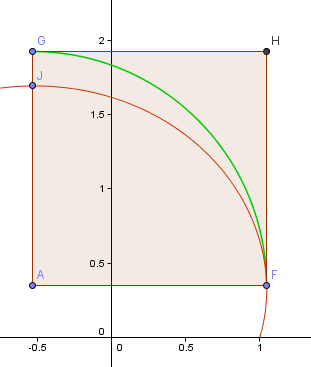
Il punto F è il punto “più a destra” della spirale, che sarà il mio punto di partenza per l’arco del quarto di giro. Il punto J è il punto più alto di questa porzione di spirale.
Il punto A è l’intersezione delle linee orizzontale e verticale che passano rispettivamente per F e J e questo sarà il centro del mio arco.
Ora, l’arco GF non è affatto vicino alla porzione relativa della spirale FJ.
Facciamo un altro passo e vediamo se la parte successiva è migliore.
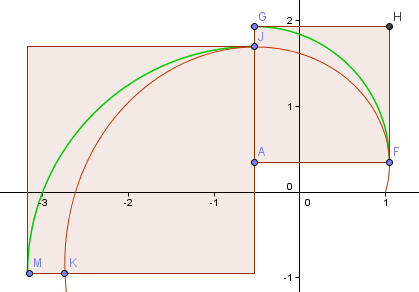
Come potete vedere, è peggio (come previsto, dato che ci siamo allontanati di più dall’origine e il braccio della spirale sta diventando più grande).
E’ chiaro che questo non funzionerà mai.
Tuttavia, nella mia precedente Spirale Aurea stavo usando:
r(t) = e0.30635t
La costante a, aveva valore 1.
Se vogliamo che i nostri archi approssimati si adattino bene alla Spirale Aurea reale, dobbiamo usare un valore di (probabilmente non sorprendente)
a = φ = 1,618103399..
Questo ci dà le seguenti curve, simili al grafico in Wikipedia.
La curva rossa è la Spirale Aurea,
r(t) = 1,618013 e0,30635t
La curva verde è l’insieme degli archi circolari.
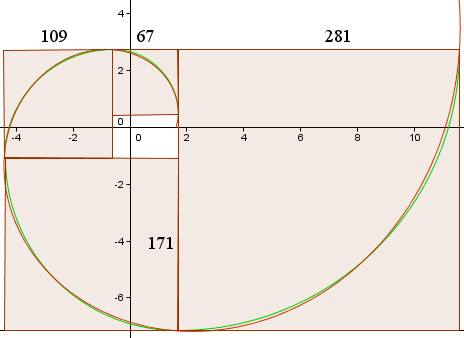
Sono mostrate le lunghezze dei lati dei quadrati (in pixel) e possiamo vedere che sono approssimativamente nel rapporto 1,618013…
La spirale dorata nella media
Da Wolfram’s Mathworld:
Nell’episodio della quarta stagione “Masterpiece” (2008) del crime drama della CBS-TV “Criminal Minds”, gli agenti dell’Unità di Analisi Comportamentale dell’FBI si confrontano con un serial killer che usa la sequenza numerica di Fibonacci per determinare il numero di vittime per ogni suo episodio di omicidio. In questo episodio, il personaggio Dr. Reid nota anche che i luoghi degli omicidi si trovano sul grafico di una spirale d’oro, e andare al centro della spirale permette a Reid di determinare la posizione della base operativa dell’assassino.
Ecco altre informazioni interessanti da Wolfram’s Mathworld:
Spirale logaritmica
Per i geek – design usando la spirale aurea
Sono in molti a credere che i design che usano il rapporto aureo e la spirale aurea siano piacevoli alla vista.
Anche Twitter ha recentemente ridisegnato la sua pagina principale usando la spirale aurea.
Qui c’è un grande articolo di un tizio che ha costruito una spirale aurea senza immagini. (Soprattutto per chi è interessato al Web design)
Spirale d’oro senza immagini – usando CSS e jQuery
Come suggerisce nell’articolo, anche la proboscide di un elefante è vicina alla spirale d’oro.

Tronco d’elefante – quasi una Spirale Aurea
Conclusione
La Spirale Aurea è un argomento interessante – uno che vale la pena seguire non solo per i piacevoli disegni coinvolti, ma anche per l’interessante matematica dietro di essi.
Spero che questo aiuti a rispondere alla tua domanda, Pehr!