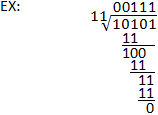A következő számológépek segítségével elvégezheti két bináris érték összeadását, kivonását, szorzását vagy osztását, valamint a bináris értékeket decimális értékekké alakíthatja, és fordítva.

Bináris számítás – összeadás, kivonás, szorzás, or Divide
Convert Binary Value to Decimal Value
Convert Decimal Value to Binary Value
Related Hex Calculator | IP Subnet Calculator
A bináris rendszer olyan számrendszer, amely gyakorlatilag ugyanúgy működik, mint az emberek által valószínűleg jobban ismert decimális számrendszer. Míg a decimális számrendszer a 10-es számot használja alapként, addig a bináris rendszer a 2-es számot. Továbbá, bár a tízes számrendszer a 0-tól 9-ig terjedő számjegyeket használja, a bináris rendszer csak 0-t és 1-et, és minden egyes számjegyet bitnek nevezünk. Ezektől a különbségektől eltekintve az olyan műveletek, mint az összeadás, kivonás, szorzás és osztás, a decimális rendszerrel azonos szabályok szerint számíthatók ki.
Szinte az összes modern technológia és számítógép a bináris rendszert használja, mivel a logikai kapuk segítségével könnyen megvalósítható a digitális áramkörökben. Sokkal egyszerűbb olyan hardvert tervezni, amelynek csak két állapotot kell érzékelnie, a be- és kikapcsolt állapotot (vagy igaz/hamis, jelen/hiányos stb.). A decimális rendszer használatához olyan hardverre lenne szükség, amely 10 állapotot képes érzékelni a 0-tól 9-ig terjedő számjegyekhez, és ez sokkal bonyolultabb.
Az alábbiakban néhány tipikus átalakítást mutatunk be a bináris és a decimális értékek között:
Bináris/Decimális átalakítás
| Decimális | Bináris |
| 0 | 0 |
| 0 | |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Míg a bináris számokkal való munka kezdetben zavarónak tűnhet, annak megértése, hogy minden bináris helyérték 2n-t jelent, ahogyan minden decimális hely 10n-t jelent, segíthet a tisztánlátásban. Vegyük például a 8-as számot. A decimális számrendszerben a 8 a tizedesponttól balra lévő első tizedesjegyen áll, ami a 100-as helyet jelenti. Ez lényegében azt jelenti:
8 × 100 = 8 × 1 = 8
Hasonlításképpen a 18-as számot használva:
(1 × 101) + (8 × 100) = 10 + 8 = 18
Binárisan a 8-at 1000-nek ábrázoljuk. Jobbról balra olvasva az első 0 a 20-at, a második a 21-et, a harmadik a 22-t, a negyedik a 23-at jelenti; ugyanúgy, mint a decimális rendszerben, csak 10 helyett 2-es bázissal. Mivel a 23 = 8, a helyére egy 1-est írunk, ami 1000-et eredményez. A 18, vagy 10010 példájával:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
A decimális rendszerről a bináris rendszerre való átváltás lépésről lépésre történik:
- Keresd meg a legnagyobb 2-es hatványt, amely az adott számon belül van
- Vond ki ezt az értéket az adott számból
- Keresd meg a legnagyobb 2-es hatványt a 2. lépésben talált maradékon belül
- Ismételd meg, amíg nincs maradék
- Írj be 1-et minden egyes megtalált bináris helyértékhez, és egy 0-t a maradékhoz
Ismét a 18-as célt használva példaként, az alábbiakban ezt egy másik módon szemléltethetjük:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instances within 18 | 1 | 0 | 0 | 1 | 0 |
| Target: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
A bináris rendszerből a decimális rendszerbe való átváltás egyszerűbb. Határozzuk meg az összes helyértéket, ahol 1 előfordul, és találjuk meg az értékek összegét.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Ezért:
Bináris összeadás
A bináris összeadás ugyanazokat a szabályokat követi, mint a decimális rendszerben az összeadás, kivéve, hogy az 1-es átvitel helyett, amikor az összeadott értékek egyenlőek 10-zel, az átvitel akkor történik, amikor az összeadás eredménye egyenlő 2-vel. A magyarázatért tekintse meg az alábbi példát.
Megjegyezzük, hogy a bináris rendszerben:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, az 1 átvitele, azaz. 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
A bináris és decimális összeadás között az egyetlen valódi különbség, hogy a bináris rendszerben a 2 érték a decimális rendszerben a 10 értéknek felel meg. Figyeljük meg, hogy a feliratos 1-es számjegyek az átvitt számjegyeket jelentik. A bináris összeadás során gyakran előforduló hiba az, amikor az 1 + 1 = 0 esetében az előző oszlopból a jobb oldali oszlopba is átvitt 1-es van. Az alsó értéknek ekkor az átvitt 1-ből 1-nek kell lennie, nem pedig 0-nak. Ez a fenti példában jobbról a harmadik oszlopban figyelhető meg.
Bináris kivonás
A bináris összeadáshoz hasonlóan a bináris és a decimális kivonás között is kevés különbség van, kivéve azokat, amelyek abból adódnak, hogy csak a 0 és 1 számjegyeket használjuk. A kölcsönzés minden olyan esetben előfordul, amikor a kivonandó szám nagyobb, mint az a szám, amelyből kivonjuk. A bináris kivonásnál csak akkor van szükség kölcsönzésre, ha 0-ból kivonunk 1-et. Ilyenkor a kölcsönzött oszlopban lévő 0 lényegében “2” lesz (a 0-1 2-1 = 1-re változik), miközben a kölcsönzött oszlopban lévő 1-et 1-gyel csökkentjük. Ha a következő oszlop is 0, akkor minden további oszlopból kölcsönzésre van szükség, amíg az 1 értékű oszlopot 0-ra nem lehet csökkenteni. A magyarázatért lásd az alábbi példát.
Megjegyezzük, hogy a bináris rendszerben:
- 0 – 0 = 0
0 – 1 = 1, 1 kölcsönzése, ami -1 átvitelt eredményez
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Megjegyezzük, hogy a megjelenített szuperindexek az egyes bitekben kölcsönzéskor bekövetkező változások. A kölcsönző oszlop lényegében 2-t kap a kölcsönzésből, és az oszlop, amelyből kölcsönöznek, 1-gyel csökken.
Bináris szorzás
A bináris szorzás vitathatatlanul egyszerűbb, mint a decimális megfelelője. Mivel csak 0 és 1 értékeket használunk, az összeadandó eredmények vagy megegyeznek az első kifejezéssel, vagy 0. Vegyük észre, hogy minden további sorban helyőrző 0-kat kell hozzáadni, és az értéket balra kell eltolni, akárcsak a tizedes szorzásnál. A bináris szorzás bonyolultsága a fárasztó bináris összeadásból adódik, amely attól függ, hogy hány bit van az egyes tagokban. Lásd az alábbi példát a tisztázás érdekében:
Megjegyezzük, hogy a bináris rendszerben:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Mint a fenti példából is látható, a bináris szorzás folyamata ugyanaz, mint a decimális szorzásé. Figyeljük meg, hogy a 0 helyőrzőt a második sorba írjuk. Általában a 0 helyőrző a tizedes szorzásnál vizuálisan nincs jelen. Bár ugyanez ebben a példában is megtehető (a 0 helyőrzőt inkább feltételezzük, mint kifejezzük), ebben a példában azért szerepel, mert a 0 releváns bármely bináris összeadás/kivonás számológép számára, mint amilyen az ezen az oldalon található. A 0 feltüntetése nélkül elkövethető lenne az a hiba, hogy a 0-t kizárjuk a fent látható bináris értékek összeadásakor. Ismét megjegyezzük, hogy a bináris rendszerben az 1-től jobbra lévő bármely 0 releváns, míg az érték utolsó 1-től balra lévő bármely 0 nem.
EX:
- 1 0 1 0 1 1 1 0 0
= 0 0 1 0 1 0 1 1 1 1 0 0
≠ 1 0 1 1 0 1 1 0 0 0 0 0
Bináris osztás
A bináris osztás folyamata hasonló a hosszú osztáshoz a decimális rendszerben. Az osztót továbbra is ugyanúgy osztjuk az osztóval, az egyetlen lényeges különbség az, hogy nem decimális, hanem bináris kivonást alkalmazunk. Vegyük figyelembe, hogy a bináris kivonás jó ismerete fontos a bináris osztás elvégzéséhez. Lásd az alábbi példát, valamint a bináris kivonásról szóló részt a magyarázatért.