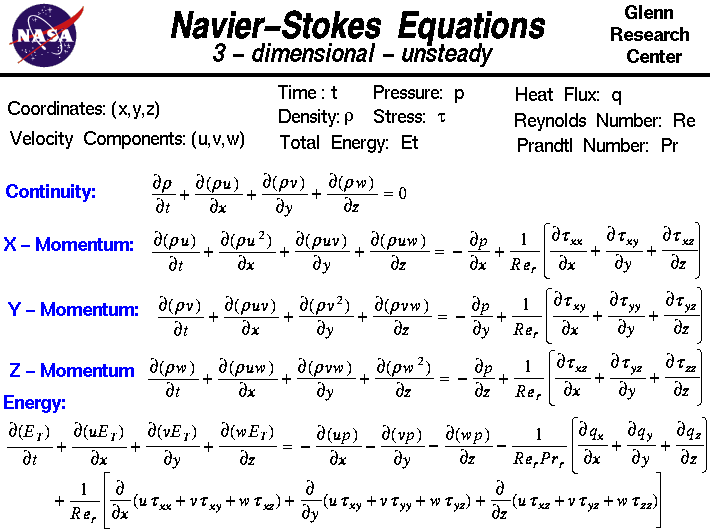
Op deze dia tonen we de driedimensionale ongestage vorm van de Navier-Stokes Vergelijkingen.Deze vergelijkingen beschrijven hoe de snelheid, druk, temperatuur en dichtheid van een bewegende vloeistof met elkaar in verband staan.De vergelijkingen werden onafhankelijk van elkaar afgeleid door G.G. Stokes, in Engeland, en M. Navier, in Frankrijk, in de vroege jaren 1800. De vergelijkingen zijn uitbreidingen van de Vergelijkingen van Euler en omvatten de effecten van viscositeit op de stroming. Deze vergelijkingen zijn zeer complex, maar aan ingenieursstudenten wordt geleerd hoe ze af te leiden in een proces dat veel lijkt op de afleiding die we presenteren op de webpagina over behoud van momentum.
De vergelijkingen zijn een stel gekoppelde differentiaalvergelijkingen en kunnen in theorie voor een gegeven stromingsprobleem worden opgelost met behulp van methoden uit de calculus.Maar in de praktijk zijn deze vergelijkingen te moeilijk om analytisch op te lossen.In het verleden hebben ingenieurs de vergelijkingen verder benaderd en vereenvoudigd totdat zij een groep vergelijkingen hadden die zij konden oplossen.Onlangs zijn computers met hoge snelheid gebruikt om benaderingen van de vergelijkingen op te lossen met behulp van een verscheidenheid van technieken zoals eindige verschillen, eindige volumes, eindige elementen en spectrale methoden.Dit studiegebied wordt Computational Fluid Dynamics of CFD genoemd.
De Navier-Stokes vergelijkingen bestaan uit een tijdsafhankelijke continuïteitsvergelijking voor massabehoud, drie tijdsafhankelijke momentbehoudsvergelijkingen en een tijdsafhankelijke energiebehoudsvergelijking.Er zijn vier onafhankelijke variabelen in het probleem, dex, y, en z ruimtelijke coördinaten van een domein, en de tijd t. Er zijn zes afhankelijke variabelen; de druk p, dichtheid r, en temperatuur T (die in de energievergelijking is vervat via de totale energie Et) en drie componenten van de snelheidsvector; de u-component is in de x-richting, de v-component in de y-richting, en de w-component in de z-richting.De differentiaalvergelijkingen zijn dus partiële differentiaalvergelijkingen en niet de gewone differentiaalvergelijkingen die je in het begin van de calculusles bestudeert.
Je zult merken dat het differentiaalsymbool anders is dan het gebruikelijke “d /dt” of “d /dx” dat je voor gewone differentiaalvergelijkingen ziet. Het symbool “
” wordt gebruikt om partiële afgeleiden aan te geven. Het symbool geeft aan dat we alle afhankelijke variabelen vast moeten houden, behalve de variabele naast het symbool, wanneer we een afgeleide berekenen. De reeks vergelijkingen zijn:
Continuïteit: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = -. p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = -. p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = -. p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energie: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
-. 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
waar Re het getal vanReynolds is, dat een gelijksoortigheidsparameter is die de verhouding is tussen de schaling van de traagheid van de stroming en de viskeuze krachten in de stroming. De q-variabelen zijn de warmtefluxcomponenten en Pr is het Prandtl-getal, dat een gelijkenisparameter is die de verhouding aangeeft tussen de visceuze spanningen en de thermische spanningen.De tau-variabelen zijn componenten van de spanningstensor.Een tensor ontstaat wanneer men twee vectoren op een bepaalde manier vermenigvuldigt. Onze snelheidsvector heeft drie componenten; de spanningstensor heeft negen componenten. Elke component van de spanningstensor is zelf een tweede afgeleide van de snelheidscomponenten.
De termen aan de linkerkant van de impulsvergelijkingen worden de convectietermen van de vergelijkingen genoemd.Convectie is een fysisch proces dat optreedt in een gasstroom waarbij een eigenschap wordt getransporteerd door de geordende beweging van de stroom.De termen aan de rechterkant van de impulsvergelijkingen die worden vermenigvuldigd met het inverse Reynoldsgetal worden de diffusietermen genoemd.Diffusie is een fysisch proces dat optreedt in een gasstroom waarin een eigenschap wordt getransporteerd door de willekeurige beweging van de moleculen van het gas.Diffusie is gerelateerd aan de spanningstensor en aan de viscositeit van het gas. Turbulentie, en het ontstaan van grenslagen, zijn het resultaat van diffusie in de stroming. De Euler vergelijkingen bevatten alleen de convectietermen van de Navier-Stokes vergelijkingen en kunnen daarom geen grenslagen modelleren. Er is een speciale vereenvoudiging van de Navier-Stokes vergelijkingen die grenslaagstromingen beschrijven.
Merk op dat alle afhankelijke variabelen in elke vergelijking voorkomen.Om een stromingsprobleem op te lossen, moet je alle vijf vergelijkingen tegelijk oplossen; daarom noemen we dit een gekoppeld stelsel van vergelijkingen.Er zijn eigenlijk nog enkele andere vergelijkingen die nodig zijn om dit stelsel op te lossen. We tonen slechts vijf vergelijkingen voor zes onbekenden. Een staticavergelijking relateert de druk, temperatuur en dichtheid van het gas.En we moeten alle termen van de spanningstensor specificeren.In CFD worden de termen van de spanningstensor vaak benaderd door een turbulentiemodel.
Activiteiten:
Rondleidingen
Navigatie ..
Beginner’s Guide Home Page