Sun, 18 Jun 2006
1+1=2
Whitehead en Russells Principia Mathematica is beroemd om de duizend pagina’s die nodig zijn om te bewijzen dat 1+1=2. Natuurlijk bewijst het ook een heleboel andere dingen. Als ze alleen hadden willen bewijzen dat 1+1=2, zou het waarschijnlijk maar half zoveel ruimte in beslag hebben genomen.
Principia Mathematica is een vreemd boek, dat zowel vanuit historisch als vanuit wiskundig oogpunt de moeite van het bekijken waard is. Het werd geschreven rond 1910, en de mathematische logica stond toen nog in de kinderschoenen, vers van de transformatie die er door Peano en Frege aan was gewerkt. De notatie is enigszins onduidelijk, omdat de wiskundige notatie sindsdien sterk is geëvolueerd. En veel van de eenvoudige technieken die we nu als vanzelfsprekend beschouwen zijn afwezig. Net als een slecht geschreven computerprogramma bestaat veel van Principia Mathematica uit herhalingscode, afzonderlijke secties die in wezen dezelfde dingen zeggen, omdat de auteurs nog niet de technieken hebben geleerd die het mogelijk zouden maken deze secties tot één geheel te combineren.
Zo begint paragraaf ∗22, “Klassenrekening”, met het definiëren van de deelverzamelingsrelatie (∗22.01), en de operaties van vereniging en doorsnijding van verzamelingen (∗22.02 en .03), het complement van een verzameling (∗22.04), en het verschil van twee verzamelingen (∗22.05). Het bewijst vervolgens de commutativiteit en associativiteit van vereniging en doorsnijding van verzamelingen (∗22.51, .52, .57,en .7), verschillende eigenschappen zoals ! (∗22.5) en dergelijke, uitmondend in stellingen als ∗22.92: ∗23 is “Relatierekening” en begint op bijna precies dezelfde manier met de definitie van de deelrelatie (∗23.01), en de operaties van relationele unie en intersectie (∗23.02 en .03), het complement van een relatie (∗23.04), en het verschil van twee relaties (∗23.05). Itlater bewijst de commutativiteit en associativiteit van relationele unie en intersectie (∗23.51, .52, .57,en .7), diverse eigenschappen zoals ! (∗22.5) en dergelijke, uitmondend in stellingen als ∗23.92: !hun eigenschappen, enzovoort, en dan wordt sectie ∗24 gedupliceerd in ∗25 in een serie stellingen over het bestaan van relaties, de null-relatie !!!, de universele relatie !!!, hun eigenschappen, enzovoort.
Zo deden Whitehead en Russell het in 1910. Hoe zouden we het vandaag de dag doen? Een relatie tussen S en T wordt gedefinieerd als een deelverzameling vanS × T en is dus een verzameling. Unie, intersectie, verschil en de andere operaties zijn voor relaties precies hetzelfde als voor verzamelingen, want relaties zijn verzamelingen. Alle stellingen over unies en intersecties van relaties, zoals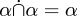 
, gaan gewoon weg, want die hebben we al bewezen voor verzamelingen en relaties zijn verzamelingen. De nul-relatie is de nul-verzameling. De universele relatie is de universele verzameling.
In 2006 verdwijnt een enorme hoeveelheid andere machinerie, vanwege de eenwording van relaties en verzamelingen. Principia Mathematica heeft een speciale notatie en een speciale definitie nodig voor het resultaat van de beperking van een relatie tot die paren waarvan het eerste element lid is van een bepaalde verzameling S, of waarvan het tweede element lid is van S, of waarvan beide elementen lid zijn van S; in 2006 zouden we gewoon de gewone doorsnedeoperatie voor verzamelingen gebruiken en het hebben over R ∩(S×B) of wat dan ook.
Whitehead en Russell konden dit in 1910 niet doen omdat een cruciaal stuk machinerie ontbrak: het geordende paar. In 1910 wist niemand hoe je een geordend paar kon samenstellen uit alleen maar logica en verzamelingen. In 2006 (of zelfs in 1956) zouden we het geordend paar <a, b> definiëren als de verzameling {{a}, {a, b}}. Dan zouden we als stelling aantonen dat <a, b> = <c, d> als en slechts als a=c en b=d, met behulp van eigenschappen van verzamelingen. Dan zouden we A×B definiëren als de verzameling van alle p zo dat p = <a,b> ∧ a ∈ A ∧ b∈ B. Dan zouden we een relatie op de verzamelingenA en B definiëren als een deelverzameling van A×B. Dan zouden we alle ∗23 en ∗25 en een heleboel ∗33 en ∗35 en ∗36 gratis krijgen, en waarschijnlijk nog een heleboel andere dingen ook.
(Tussen haakjes, het {{a}, {a, b}} ding is uitgevonden door Kuratowski. Het wordt meestal toegeschreven aan Norbert Wiener, maar Wiener’s idee, hoewel vergelijkbaar, was eigenlijk ingewikkelder.)
Er zijn geen geordende paren in Principia Mathematica, behalve impliciet. Er zijn zelfs nauwelijks verzamelingen. Whitehead en Russell willen alles baseren op logica. Voor Whitehead en Russell is het fundamentele begrip de “propositionele functie”, dat is een functie φ waarvan de uitgang een waarheidswaarde is. Voor elke functie is er een bijbehorende verzameling, die zij aanduiden met φ(x)!!, de verzameling van alle x zodat φ(x) waar is. Voor Whitehead en Russell wordt een vergelijking geïmpliceerd door een propositionele functie van twee variabelen, analoog aan de manier waarop een verzameling wordt geïmpliceerd door een propositionele functie van één variabele. In 2006 zien we af van “functies van twee variabelen”, en spreken we gewoon over functies waarvan het (enige) argument een geordend paar is; een relatie wordt dan de verzameling van alle geordende paren waarvoor een functie waar is.
Russell zou gezegd hebben dat de ontdekking van de Shefferstroke (een enkele logische operator van waaruit alle andere logische operatoren kunnen worden opgebouwd) een enorme vooruitgang was, en alles zou veranderen. Dit komt ons nu vreemd voor, omdat de ontdekking van de Sheffertakt zo eenvoudig lijkt, en het verandert werkelijk niets belangrijks. Je hoeft alleen maar aan het begin van hoofdstuk 1 een noot toe te voegen waarin staat dat ∼p en p∨q afkortingen zijn voor respectievelijk p|p en p|p.|.q|q, de vijf fundamentele axioma’s te bewijzen, en verder alles bij het oude te laten. Maar Russell zou met enig recht hetzelfde gezegd kunnen hebben over de ontdekking dat geordende paren geïnterpreteerd kunnen worden als verzamelingen, een eenvoudige ontdekking die de Principia Mathematica werkelijk in een heel ander werk zou hebben veranderd.
Hoe dan ook, met die achtergrond op zijn plaats, kunnen we hetPrincipia Mathematica bewijs van 1+1=2 bespreken. Dit komt vrij laat in de Principia Mathematica voor, in sectie 102. Mijn verkorte versie gaat maar tot ∗56, maar dat is ver genoeg om tot de belangrijke voorloperstelling te komen, ∗54.43, hieronder gescand:
De notatie kan overweldigend zijn, dus laten we ons alleen concentreren op de stelling, al het andere negeren, zelfs de nuttige opmerking onderaan:
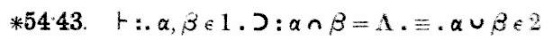
Dit is de stelling die bewezen wordt; wat volgt is het bewijs.
Nu moet ik de notatie uitleggen, die enigszins veranderd is sinds1910. Ten eerste, Principia Mathematica gebruikt Peano’s “punten” notatie om de voorrang te ontcijferen, waar we nu haakjes gebruiken. De puntnotatie is even wennen, maar heeft een aantal duidelijke voordelen ten opzichte van de haakjes. Het idee is gewoon dat je groepering aangeeft door punten in te voegen, zodat (1+2)×(3+4)×(5+6) wordt geschreven als1+2.×.3+4.×.5+6. De middelste subformule staat tussen een aantal punten. De subformule (1+2) staat ook tussen een paar puntjes, maar het puntje aan de linkerkant is overbodig en laten we weg; op dezelfde manier wordt de subformule (5+6) afgebakend door een puntje aan de linkerkant en door het einde van de formule aan de rechterkant.
Wat als je haakjes moet nesten? Dan gebruik je meer punten. Een dubbele punt (:) is als een enkele punt, maar sterker. We schrijven bijvoorbeeld ((1+2)×3)+4 als 1+2 . × 3 : + 4, en het dubbele puntje isoleert de hele 1+2 . × 3 uitdrukking in een enkele deel-formule waarop de +4 van toepassing is.
Soms heb je meer niveaus van voorrang nodig, en dan gebruik je tripledots (.: en :.) en quadruple (::). Deze formule heeft, zoals je ziet, dubbele en driedubbele punten. Als we de punten omzetten in standaardparenthese-notatie, krijgen we $54,43. \((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$. Dit ziet er wat rommeliger uit dan de versie met de punten, en bij ingewikkelde formules kun je moeite hebben om uit te zoeken welke haakjes bij welke passen. Met de punten is het altijd gemakkelijk. Ik vind het dus een beetje jammer dat deze conventie in onbruik is geraakt.
Het symbool Λ is niet veranderd; het betekent dat de formule waarop het van toepassing is, als waar wordt beschouwd. Λ is logische implicatie, en Λ is logische equivalentie. Λ is de lege set, die we tegenwoordig schrijven als ∅. ∩ ∪ en ∈ hebben hun moderne betekenis: ∩ en ∪ zijn de set intersection en de union operatoren, en x∈y betekent dat x een element is van set y.
De overige punten zijn semantisch. α en β zijn verzamelingen. 1 staat voor de verzameling van alle verzamelingen die precies één element hebben. Dat wil zeggen, de verzameling { c : er bestaat a zodat c = {a } }. Stellingen over 1 zijn bijvoorbeeld:
- dat Λ∉1 (∗52.21),
- dat als α∈1 dan is er een zekere x zodanig dat α ={x} (∗52.1), en
- dat {x}∈1 (∗52.22).
2 is op dezelfde manier de verzameling van alle verzamelingen die precies twee elementen hebben. Een belangrijke stelling over 2 is ∗54.3, die $$$54.3 zegt. \vdash 2 = (x bestaat) \> .\3977>x \in\alpha \3977> . \
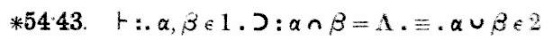
De stelling luidt dat als de verzamelingen α en β elk precies één element hebben, zij disjunct zijn (d.w.z. geen gemeenschappelijke elementen hebben) als en slechts als hun unie precies twee elementen heeft.
Het bewijs, dat in de scan hierboven staat na het woord “Dem.” (kort voor “demonstratie”), gaat als volgt:
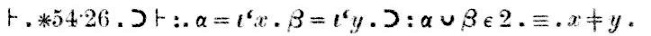
“Stelling ∗54.26 houdt in dat als α = {x} en β = {y}, danα∪β 2 elementen heeft als en slechts als x verschillend is van y.”
“Volgens stelling ∗51.231 is dit laatste (x is verschillend vany) waar als en slechts als {x} en {y} ongelijk zijn.”
“Volgens ∗13.12 is dit laatste stukje ({x} en {y} zijn disjunct) waar als en slechts als α en β zelf disjunct zijn.” De deelconclusie op dit punt, die is gelabeld met (1), is dat als α = {x} en β = {y}, dan α∪β ∈ 2 als en slechts alsα∩β = Λ.
Het bewijs gaat verder: “Conclusie (1), met de stellingen ∗11.11 en ∗11.35,impliceert dat als er x en y bestaan zodat α is{x} en β is {y}, dan α∪β ∈ 2 als en slechts als α en β disjunct zijn.” Deze conclusie wordt gelabeld als (2).
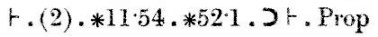
Tot slot, conclusie (2), samen met de stellingen ∗11.54 en ∗52.1, impliceert de stelling die we probeerden te bewijzen.
Misschien valt hier op hoe klein de stapjes zijn.∗54.26, waar deze stelling sterk van afhangt, is bijna hetzelfde; zij stelt dat {x}∪{y} ∈ 2 als en slechts als x≠y. ∗54.26 hangt op zijn beurt af van ∗54.101, die zegt dat α 2 elementen heeft als en slechts als er x eny bestaan, niet dezelfde, zodat α = {x} ∪{y}. ∗54.101 is maar een heel klein beetje anders dan de definitie van 2. Stelling ∗51.231 zegt dat {x} en {y} ongelijk zijn als en slechts als x en y verschillend zijn.∗52.1 is een basiseigenschap van 1; we zagen het al eerder.
De andere stellingen die in de demonstratie worden aangehaald zijn heel kleine technische dingetjes. ∗11.54 zegt dat je een bewering dat twee dingen bestaan, kunt splitsen in twee beweringen, die elk beweren dat een van de dingen bestaat. ∗11.11 is nog slanker: het zegt dat als φ(x, y) altijd waar is, dan kun je er een universele kwantor aan koppelen, en beweren dat φ(x, y) waar is voor alle x en y. ∗13.12 betreft de vervanging van gelijken door gelijken: als x en y gelijk zijn, dan bezit x een eigenschap ψ als en slechts als y die ook bezit. Ik heb de latere delen van Principia Mathematica nog niet gezien, want mijn exemplaar stopt na hoofdstuk 56, en het rekenkundige gedeelte is veel later. Maar deze stelling heeft duidelijk de betekenis van 1+1=2 in zich, en de latere stelling (∗110.643)die eigenlijk 1+1=2 beweert hangt sterk van deze stelling af.
Hoewel ik niet helemaal zeker weet wat er later gaat gebeuren (ik heb hier al veel te veel tijd aan verspild om er nog meer tijd in te steken om de volledige versie uit de bibliotheek te halen) kan ik wel een beredeneerde gok maken. Principia Mathematica gaat het getal 17 definiëren als de verzameling van alle verzamelingen van 17 elementen, en evenzo voor elk ander getal; het gebruik van het symbool 2 om de verzameling van alle verzamelingen van 2 elementen voor te stellen is hier een voorbode van. De verzamelingen van alle verzamelingen van een bepaalde grootte worden dan aangeduid als de “kardinale getallen”.
In de Principia Mathematica zal de som van kardinale getallen p en q als volgt worden gedefinieerd: neem een representatieve verzameling a uit p;a heeft p elementen. Neem een representatieve verzameling b uit q; b heeft q elementen. Zij c =a∪b. Als c lid is van een of ander kardinaal getal r, en als a en b disjunct zijn, dan is de som van p en q r.
Met deze definitie kun je de gebruikelijke wenselijke eigenschappen van optellen bewijzen, zoals x + 0 = x, x + y = y + x, en 1 + 1 = 2.
In het bijzonder volgt 1+1=2 direct uit stelling ∗54.43; het is precies wat we willen, want om 1+1 te berekenen, moeten we twee aaneengesloten representanten van 1 vinden, en hun unie nemen; ∗54.43 stelt dat de unie een element van 2 moet zijn, ongeacht welke representanten we kiezen, zodat 1+1=2.
Post scriptum: Peter Norvig zegt dat de circumflex in de PRincipia Mathematica notatie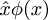 
de uiteindelijke bron is van het gebruik van het woord lambda om een anonieme functie aan te duiden in de programmeertalen Lisp en Python. U weet ongetwijfeld dat deze talen “lambda” ontlenen aan het gebruik van de Griekse letter λ door Alonzo Church om functie-abstractie weer te geven in zijn “λ-calculus”: In Lisp is(lambda (u) B) een functie die een argumentu neemt en de waarde van B teruggeeft; in de λ-calculus is λu.B een functie die een argumentu neemt en de waarde van B teruggeeft. Norvig zegt dat Church oorspronkelijk van plan was de functieλu.B als û.B te schrijven, maar zijn printer kon geen circumflex-accenten aanbrengen. Dus overwoog hij het circonflexe naar links te verplaatsen en in plaats daarvan een hoofdletter lambda te gebruiken: Λu.B. De hoofdletter Λ leek te veel op logica en ∧, wat verwarrend was, dus gebruikte hij in plaats daarvan kleine letters lambdaλ.
Post post scriptum: Iedereen zegt altijd “Russell en Whitehead”. De Google-resultaten voor “Russell en Whitehead” zijn bijvoorbeeld twee keer zo groot als die voor “Whitehead en Russell”. Waarom? Op de omslag en de titelpagina staat “Alfred North Whitehead and Bertrand Russell, F.R.S.”. Hoe en wanneer heeft Whitehead de eerste plaats verloren?
permanente link