- Leerdoelen
- Netten
- Voorbeeld 1
- Voorbeeld 2
- Oefeningen
- Antwoorden
- Prisma’s
- Oppervlakte van een prisma met behulp van netten
- Voorbeeld 3
- Herhalingsoefeningen
- Antwoorden
- Cilinders
- Oppervlakte van een cilinder met behulp van netten
- Voorbeeld 4
- Oppervlakte van een cilinder met behulp van een formule
- Voorbeeld 5
- Voorbeeld 6
- Voorbeeld 7
- Bollen
- Oppervlakte van een bol
- Voorbeeld 8
- Voorbeeld 9
- Oefeningen
- Antwoorden
Leerdoelen
- Netten begrijpen.
- Netten gebruiken om prisma’s voor te stellen.
- De oppervlakte van een prisma bepalen.
- De oppervlakte van cilinders bepalen.
- De oppervlakte van een bol bepalen.
Netten
Een laatste manier om een vaste stof weer te geven is door een net te gebruiken. Als je een net uitknipt, kun je het vouwen tot een model van een figuur. Netten kunnen ook worden gebruikt om een enkel massief te analyseren. Hier is een voorbeeld van een net voor een kubus.
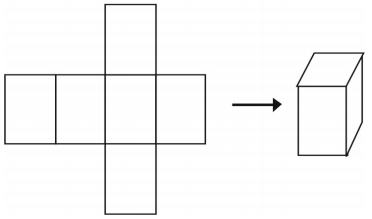
Er is meer dan één manier om een net te maken voor een enkele figuur.
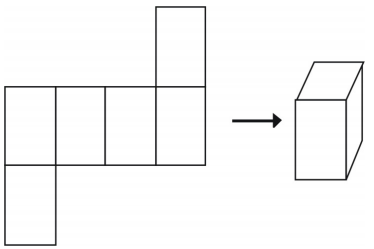
Niet alle opstellingen zullen echter een kubus opleveren.
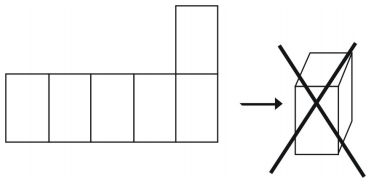
Voorbeeld 1
Wat voor figuur levert het net op? Teken de figuur.
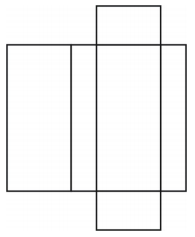
Het net creëert een doosvormig rechthoekig prisma zoals hieronder is afgebeeld.
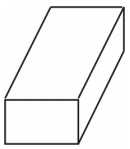
Voorbeeld 2
Welk soort net kun je tekenen om de afgebeelde figuur weer te geven? Teken het net.
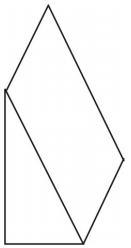
Een net voor het prisma is afgebeeld. Andere netten zijn mogelijk.
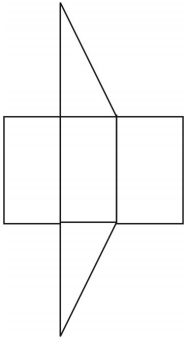
Oefeningen
Teken een net voor elk van de volgende:
Antwoorden
Prisma’s
Een prisma is een driedimensionale figuur met een paar evenwijdige en congruente uiteinden, of bases. De zijden van een prisma zijn parallellogrammen. Prisma’s worden geïdentificeerd aan de hand van hun bases.
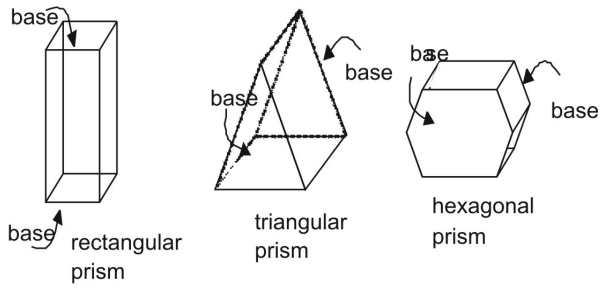
Oppervlakte van een prisma met behulp van netten
De prisma’s hierboven zijn rechtse prisma’s. In een recht prisma staan de laterale zijden loodrecht op de grondvlakken van het prisma. Vergelijk een recht prisma met een schuin prisma, waarbij de zijden en grondvlakken niet loodrecht op elkaar staan.
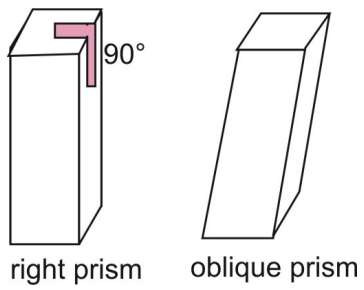
Twee postulaten die van toepassing zijn op oppervlakte zijn het Oppervlakte Congruentie Postulaat en het Oppervlakte Toevoeging Postulaat.
Je kunt een net en het Oppervlakte Optelpostulaat gebruiken om de oppervlakte van een recht prisma te vinden.
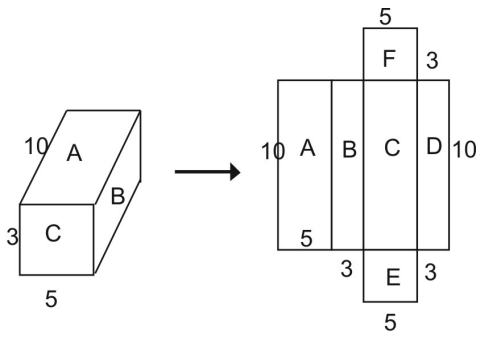
U kunt uit het net aflezen dat de oppervlakte van het hele prisma gelijk is aan de som van de figuren die het net vormen:
Totale oppervlakte = oppervlakte A + oppervlakte B + oppervlakte C + oppervlakte D + oppervlakte E + oppervlakte F
Uit de formule voor de oppervlakte van een rechthoek kunt u afleiden dat de oppervlakte van rechthoek A is:
A = l – b
A = 10 – 5 = 50 vierkante eenheden
Op dezelfde manier worden de oppervlakten van de andere rechthoeken weer in de bovenstaande vergelijking ingevoegd.
Totale oppervlakte = oppervlakte A + oppervlakte B + oppervlakte C + oppervlakte D + oppervlakte E + oppervlakte F
Totale oppervlakte = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 3)
Totale oppervlakte = 50 + 30 + 50 + 30 + 15 + 15
Totale oppervlakte = 190 vierkante eenheden
Voorbeeld 3
Gebruik een net om de oppervlakte van het prisma te vinden.
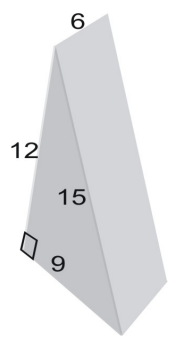
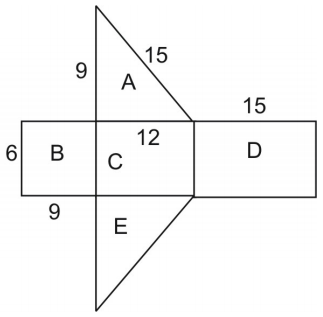
De oppervlakte van het net is gelijk aan de oppervlakte van de figuur. Om de oppervlakte van de driehoek te vinden, gebruiken we de formule:
Hierbij is h de hoogte van de driehoek en b de basis.
Merk op dat de driehoeken A en E congruent zijn, zodat we de oppervlakte van driehoek A met 2 kunnen vermenigvuldigen.
Displaystyle:oppervlakte=2(\text{area }A)++\text{area }B+\text{area }C+\text{area }D+\text{area }E)
Displaystyle:\text{area }=2(\text{area }A)++\text{area } }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, is de oppervlakte 324 vierkante eenheden.
Herhalingsoefeningen
Voor elk van het volgende vind je de oppervlakte zijn a met behulp van de methode van netten en de omtrek


- Het grondvlak van een prisma is een rechthoekige driehoek waarvan de benen 3 en 4 zijn en de hoogte 20 is. Wat is de totale oppervlakte van het prisma?
- Een rechts zeshoekig prisma is 24 inch hoog en heeft een basis van regelmatige zeshoeken van 8 inch aan één zijde. Wat is de totale oppervlakte?
- Wat is het volume van het prisma in opgave 4?
In de volgende vragen heeft een schuur de vorm van een vijfhoekig prisma met afmetingen in voeten:

- Hoeveel vierkante voeten (exclusief het dak) zijn er op het te schilderen oppervlak van de schuur?
- Als een gallon verf 250 vierkante meter beslaat, hoeveel gallon verf is er dan nodig om de schuur te schilderen?
- Een kartonnen doos is een perfecte kubus met een rand van 15 cm. Hoeveel kubieke meter kan er in?
- Een zwembad is 1 meter breed, 2 meter lang en gelijkmatig 1 meter diep. Hoeveel kubieke meter water kan er in?
- Een cornflakesdoos is 25 cm lang, 9 cm breed en 30 cm hoog. Hoeveel graan kan er in?
Antwoorden
Netten en omtrek:
- 40,5 in2
- 838 cm2
- 252 vierkante eenheden
- 1484.6 vierkante eenheden
- 3990,7 kubieke centimeter
De schuur:
- 2450 vierkante voet
- 10 liter verf
- 2,85 kubieke voet (wees hier voorzichtig. De eenheden in de opgave zijn gegeven in inches, maar de vraag vraagt om feet.)
- 2048 cubic feet
- 6750 cm3
Cilinders
Een cilinder is een driedimensionale figuur met een paar evenwijdige en congruente cirkelvormige uiteinden, of bases. Een cilinder heeft een enkele gekromde zijde die bij platlegging een rechthoek vormt.
Zoals bij prisma’s kunnen cilinders recht of schuin zijn. De zijde van een rechtse cilinder staat loodrecht op de cirkelvormige basis. De zijde van een schuine cilinder staat niet loodrecht op de bases.
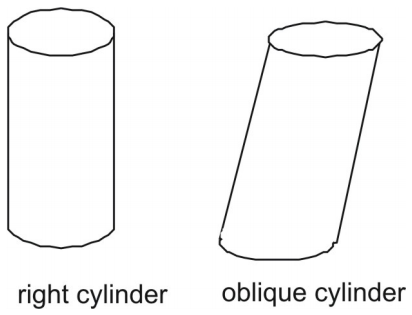
Oppervlakte van een cilinder met behulp van netten
Je kunt een cilinder ontleden tot een net.
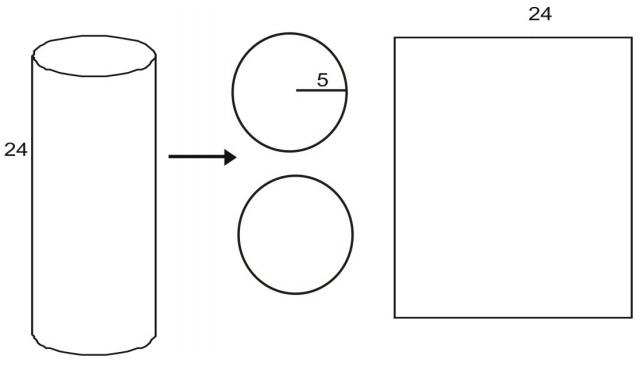
De oppervlakte van elk grondvlak wordt gegeven door de oppervlakte van een cirkel:
A={r}^2
A=(5)^2
A=25(25)(3,14)=78,5
De oppervlakte van het rechthoekige zijvlak L wordt gegeven door het product van een breedte en een hoogte. De hoogte is gegeven als 24. Je ziet dat de breedte van de oppervlakte gelijk is aan de omtrek van de cirkelvormige basis.
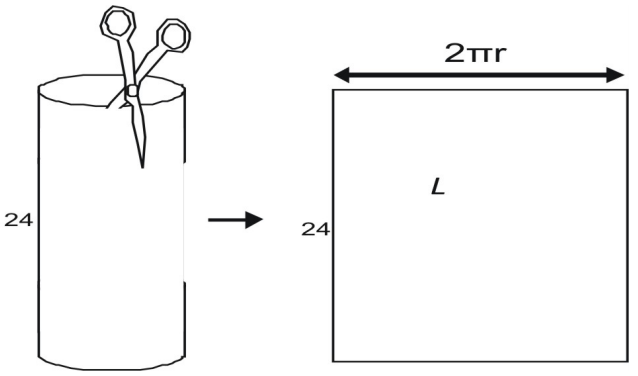
Om de breedte te vinden, stel je voor dat je een blikachtige cilinder met een schaar uit elkaar haalt. Als je de laterale oppervlakte afknipt, zie je dat deze gelijk is aan de omtrek van de bovenkant van het blikje. De omtrek van een cirkel is gegeven door C = 2πr, de zijdelingse oppervlakte, L, is
L=2{³(5)(24)
L=2{³(5)(24)
L=240{³(240)(3.14)=753,6
Nu kunnen we de oppervlakte van de hele cilinder vinden met A = (oppervlakte van twee grondvlakken) + (oppervlakte van de laterale zijde).
A=2(75,36)+753,6
A=904,32
U ziet dat de formule die we hebben gebruikt om de totale oppervlakte te vinden, voor elke rechte cilinder kan worden gebruikt.
Voorbeeld 4
Gebruik een net om de oppervlakte van de cilinder te vinden.
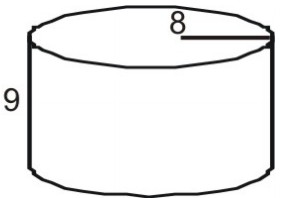
Teken en etiketteer eerst een net voor de figuur.
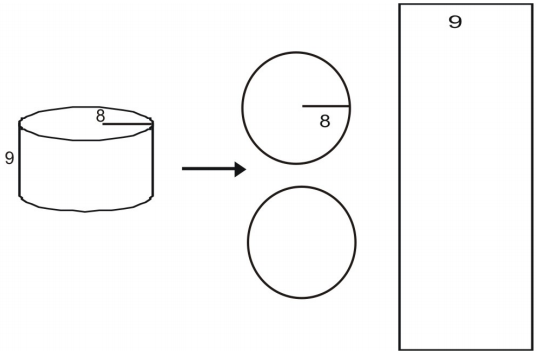
Bereken de oppervlakte van elk grondvlak.
A=(8)^2A=(8)^2>
A=(64)^2(3.14)=200.96>
A=(8)^2(3.14)=200.9614)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16
Bepaal de oppervlakte van de hele cilinder.
A=2(200.96)+452.16
A=854.08
Dus de totale oppervlakte is ongeveer 854,08 vierkante eenheden
Oppervlakte van een cilinder met behulp van een formule
Je hebt gezien hoe je netten kunt gebruiken om de totale oppervlakte van een cilinder te vinden. Het postulaat kan worden uitgesplitst om een algemene formule te maken voor alle rechte cilinders.
A = 2B + L

Merk op dat het grondvlak, B, van een willekeurige cilinder is: B = πr2
Het laterale oppervlak, L, voor een willekeurige cilinder is:
L=:breedte van de laterale oppervlakte}
L=:omtrek van het grondvlak}
L=2:pi{r}
De twee vergelijkingen samengevoegd krijgen we:
Factoren van a uit de vergelijking geeft:
De oppervlakte van een rechte cilinder: Een rechte cilinder met straal r en hoogte h kan worden uitgedrukt als:
A = 2πr2 + 2πrh
of:
A = 2πr(r + h)
Je kunt de formules gebruiken om de oppervlakte van een willekeurige rechte cilinder te vinden.
Voorbeeld 5
Gebruik de formule om de oppervlakte van de cilinder te vinden.
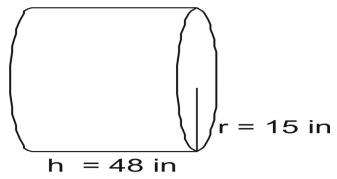
Schrijf de formule en vul de waarden in en los op.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.
Voorbeeld 6
Vind de oppervlakte van de cilinder.
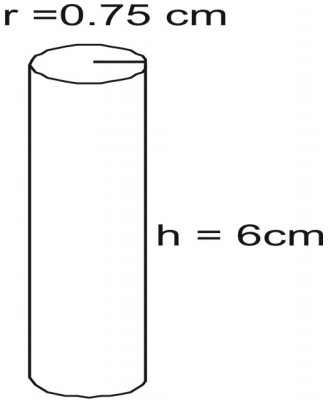
Schrijf de formule en vul de waarden in en los op.
A=2(r+h)-pi{r}(r+h)-A=2(3,14)(0,75)-A=31.7925 Vierkante inches
Voorbeeld 7
Vind de hoogte van een cilinder met een straal van 4 cm en een oppervlakte van 226,08 cm².
Schrijf de formule met de gegeven informatie en los op voor h.
A=2(3,14)(4)‛(r+h)‛226,08=2(3,14)(4)‛226,08=25,12‛226,08=100,48+25,12h‛5=h‛
Bollen
Een bol is een driedimensionale figuur die de vorm heeft van een bol.

Bollen kunnen op drie manieren worden gekarakteriseerd.
- Een bol is de verzameling van alle punten die op een vaste afstand r van een enkel middelpunt O liggen.
- Een bol is het oppervlak dat ontstaat als een cirkel om een van zijn diameters wordt gedraaid.
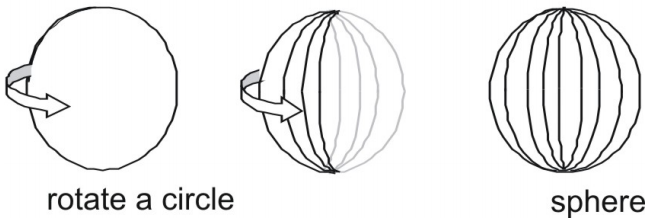
Oppervlakte van een bol
U kunt de formule voor de oppervlakte van een bol afleiden door metingen te verrichten aan bollen en cilinders. Hier tonen we een bol met een straal van 3 en een rechter cilinder met zowel een straal als een hoogte van 3 en drukken we de oppervlakte uit in termen van π.
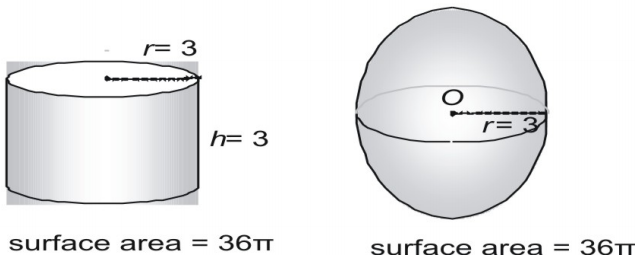
Nu proberen we een groter paar, waarbij we de oppervlakte in decimale vorm uitdrukken.
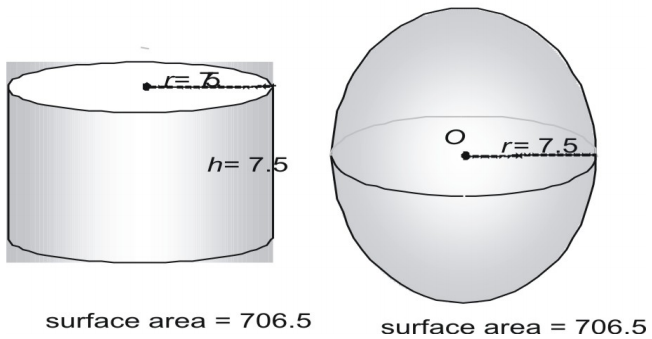
Kijk eens naar een derde paar.
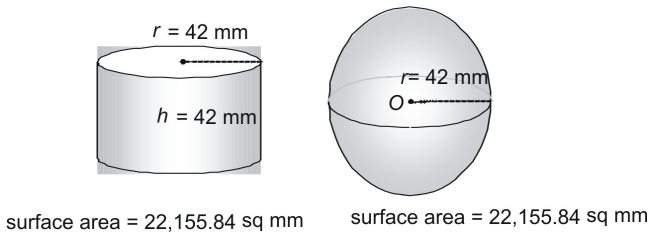
Is het toeval dat een bol en een cilinder waarvan de straal en hoogte gelijk zijn aan de straal van de bol precies dezelfde oppervlakte hebben? Helemaal niet! In feite gebruikten de oude Grieken een methode die aantoonde dat de volgende formule kan worden gebruikt om de oppervlakte van elke bol (of elke cilinder waarin ) te vinden.
Voorbeeld 8
Bepaal de oppervlakte van een bol met een straal van 14 voet.
Gebruik de formule.
A=4\pi{r}^2}A=4\pi(14)^2}
A=4\pi(196)^
A=784\pi{3543>2461.76 vierkante voet met behulp van 3,14 voor ^
Voorbeeld 9
Bepaal de oppervlakte van de volgende figuur in termen van π.
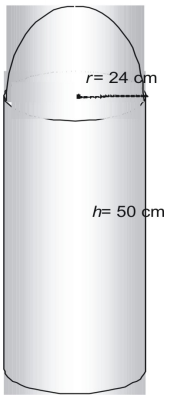
De figuur bestaat uit een halve bol of halve bol, en een cilinder zonder top.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half bol})=2pi(576)3543>A(halve bol})=1152 vierkante cm}
Nu de oppervlakte van de cilinder zonder top berekenen.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, de totale oppervlakte is 1152%+2976%=4128%
Oefeningen
- Bepaal de straal van de bol die een volume heeft van 335 cm3.
- Bepaal de oppervlakte en het volume van deze vorm:

- De straal van een bol is 4. Bereken het volume en de totale oppervlakte.
- Een bol heeft een straal van 5. Een rechte cilinder met dezelfde straal heeft hetzelfde volume. Bereken de hoogte en de totale oppervlakte van de cilinder.
- Sfeer: volume = 296 cm3. Bereken de diameter.
- Sfeer: de oppervlakte is 179 in2. Bereken de straal.
- Tennisballen met een diameter van 3,5 inch worden verkocht in blikken van drie. Het blikje is een cilinder. Neem aan dat de balletjes het blikje aan de zijkanten, bovenkant en onderkant raken. Wat is het volume van de ruimte die niet door de tennisballen wordt ingenomen?
- Een bol heeft een oppervlakte van 36π in2. Bereken het volume.
- Een reusachtige schep, bediend door een kraan, heeft de vorm van een halve bol met straal = 21 inch. De schep is gevuld met gesmolten heet staal. Als het staal in een cilindrische opslagtank wordt gegoten met een straal van 28 inch, zal het gesmolten staal stijgen tot een hoogte van hoeveel inch?
Antwoorden
Merk op dat in deze problemen π wordt gebruikt en niet 3,14.
- 1. Straal = 4,31 cm
- Oppervlakte = 706,86 cm2
Volume = 1767,15 cm3 - Volume = 268,08 eenheden3
Oppervlakte = 201,06 eenheden2 - Hoogte = 20/3 eenheden totale oppervlakte = 366,52 eenheden2
- Diameter = 8,27cm
- Radius = 3.77 inches
- Inhoud cilinder = 32.16π in3 inhoud tennisballen = 21.44π in3
Inhoud ruimte niet ingenomen door tennisballen = 33.68 in3 - Inhoud = 113.10 in3
- Hoogte gesmolten staal in cilinder zal 7.88 inches
zijn.



