Ciśnienie wskazuje siłę normalną na jednostkę powierzchni w danym punkcie działającą na danej płaszczyźnie. Ponieważ w płynie w stanie spoczynku nie występują naprężenia ścinające – ciśnienie w płynie jest niezależne od kierunku.
Dla płynów – cieczy lub gazów – w stanie spoczynku gradient ciśnienia w kierunku pionowym zależy tylko od ciężaru właściwego płynu.
Jak zmienia się ciśnienie wraz z wysokością w płynie można wyrazić jako
Δp = – γ Δh (1)
gdzie
Δp = zmiana ciśnienia (Pa, psi)
Δh = zmiana wysokości (m, in)
γ = ciężar właściwy płynu (N/m3, lb/ft3)
Gradient ciśnienia w kierunku pionowym jest ujemny – ciśnienie maleje ku górze.
Ciężar właściwy
Ciężar właściwy płynu można wyrazić jako:
γ = ρ g (2)
gdzie
ρ = gęstość płynu (kg/m3, ślimaki/ft3)
g = przyspieszenie ziemskie (9.81 m/s2, 32.174 ft/s2)
W ogólności ciężar właściwy – γ – jest stały dla płynów. Dla gazów ciężar właściwy – γ – zmienia się wraz z wysokością (i kompresją).
Ciśnienie wywierane przez płyn statyczny zależy tylko od
- głębokości płynu
- gęstości płynu
- przyspieszenia siły ciężkości
Ciśnienie statyczne w płynie
Dla płynu nieściśliwego – jak ciecz – różnica ciśnień między dwoma wzniesieniami może być wyrażona jako:
Δp = p2 – p1
= – γ (h2 – h1) (3)
gdzie
p2 = ciśnienie na poziomie 2 (Pa, psi)
p1 = ciśnienie na poziomie 1 (Pa, psi)
h2 = poziom 2 (m, ft)
h1 = poziom 1 (m, ft)
(3) można przekształcić do:
Δp = p1 – p2
= γ (h2 – h1) (4)
lub
p1 – p2 = γ Δh (5)
gdzie
Δh = h2 – h1 = różnica wzniesień – spadek z miejsca h2 do h1 (m, ft)
lub
p1 = γ Δh + p2 (6)
Przykład – ciśnienie w cieczy
Ciśnienie bezwzględne w wodzie na głębokości 10 m można obliczyć jako:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 lub Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
gdzie
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = ciśnienie na poziomie powierzchni = ciśnienie atmosferyczne = 101,3 kPa
Ciśnienie manometryczne można obliczyć, ustawiając p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98.1 kPa
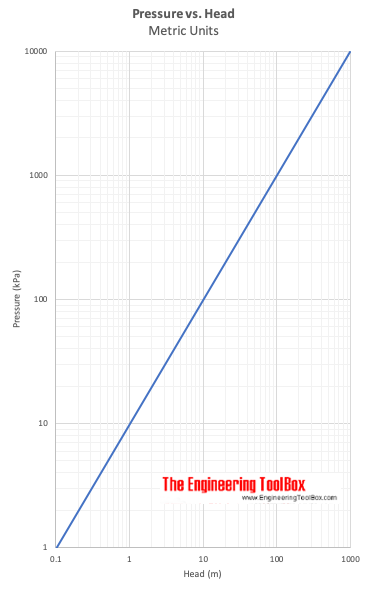
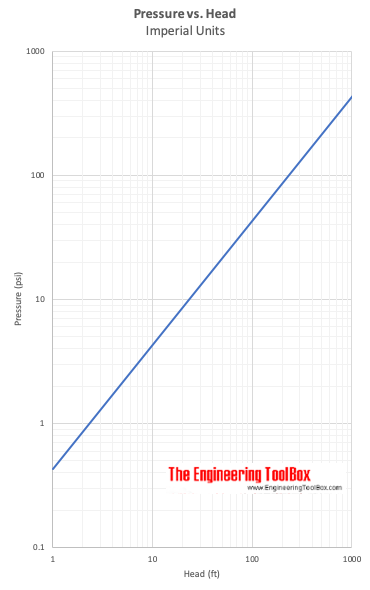
Pressure vs. Head
(6) można przekształcić na:
Δh = (p2 – p1) / γ (7)
Δh wyrażają głowicę – różnicę wysokości słupa cieczy o ciężarze właściwym – γ – potrzebną do uzyskania różnicy ciśnień Δp = p2 – p1.
Przykład – Pressure vs. Head
Różnica ciśnień wynosząca 5 psi (lbf/in2) jest równoważna głowicy w wodzie
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11,6 ft wody
lub głowa w rtęci
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0,85 ft rtęci
Ciężar właściwy wody wynosi 62.4 (lb/ft3), a ciężar właściwy rtęci wynosi 847 (lb/ft3).
- Prędkość – ciśnienie dynamiczne vs. wysokość
.