
Fern
Oto ostatnie pytanie od czytelnika Pehr ze Szwecji:
Hi,
Po pierwsze, wspaniała strona. Uwielbiam ją.
Studiowałem sekcję o współrzędnych biegunowych, mając nadzieję na poszerzenie mojej wiedzy na temat spirali równoramiennej. Interaktywne narzędzia są świetne, choć mam problem z dokładnym matematycznym rozwiązaniem, dlaczego wynikowa funkcja dla złotej spirali to
r = ae^(b(theta))
Dla niektórych tła na pytanie Pehra, zobacz:
Współrzędne biegunowe, krzywe we współrzędnych biegunowych i spirala równoramienna
Spirale są powszechne w przyrodzie i inspirowały matematyków przez wieki.

Spirala aloesu

Galaktyka spiralna NGC 5194
Spirale logarytmiczne
Złota spirala, o którą pyta Pehr, jest szczególnym przypadkiem spirali logarytmicznej.
Spirale logarytmiczne rosną w taki sposób, że kąt prostej od środka spirali do stycznej do krzywej w tym punkcie jest stały. Z tego powodu są one również znane jako spirale „równokątne”.
Aby zobaczyć, co to oznacza, 3 kąty ostre zaznaczone na poniższym obrazie paproci mają kąt około 80°

Spirala równokątna
Przy opisywaniu spirali zwykle używamy funkcji we współrzędnych biegunowych. W przeciwnym razie, jeśli używamy zwykłych współrzędnych prostokątnych, wzory stają się bardzo skomplikowane.
Wzór na spiralę logarytmiczną przy użyciu współrzędnych biegunowych to:
r = aeθ cot b
gdzie
r jest odległością od początku (lub „bieguna”)
a jest stałą
θ jest kątem (w radianach) od osi poziomej. Zatem współrzędne punktu na krzywej we współrzędnych biegunowych są dane przez (r, θ).
b jest kątem (w radianach – kąt „równy”), jaki prosta ze środka spirali tworzy ze styczną do spirali. W przypadku paproci, b ≈ 1,4 radianów (≈ 80°).
W konsekwencji sposobu, w jaki zdefiniowaliśmy spiralę logarytmiczną, stosunek odległości od środka do każdego z ramion spiralnych sąsiadującej pary jest stały.

Ramiona spiralne w stałym stosunku
Stosunek
odległość do pierwszego ramienia: odległość do drugiego ramienia
= 29:69
≈ 0.42
Drugi stosunek
odległość do drugiego ramienia: odległość do trzeciego ramienia
= 69:154
≈ 0.45
Widzimy, że te stosunki są prawie takie same. (W rzeczywistej spirali logarytmicznej są one dokładnie takie same. Wybór punktu początkowego dla paproci nie jest nauką ścisłą)!
Złota spirala
Złota spirala jest szczególnym przypadkiem spirali logarytmicznej.
Ogólną spiralę logarytmiczną możemy zapisać jako funkcję we współrzędnych biegunowych z użyciem t w następujący sposób:
r(t) = aet cot b
Uwaga: Normalnie używamy θ jako zmiennej niezależnej, ale często używamy t, ponieważ możemy myśleć o spirali, która jest śledzona w czasie. Poza tym, jest to łatwiejsze do wpisania!
Złota spirala ma tę szczególną własność, że dla każdego 1/4 obrotu (90° lub π/2 w radianach), odległość od środka spirali wzrasta o złotą proporcję φ = 1.6180.
Aby to nastąpiło, cot b musi przyjąć wartość (która pochodzi z rozwiązania naszej funkcji):
![]()
Używając tej wartości i przyjmując prosty przypadek, w którym a = 1, nasza funkcja staje się:
r(t) = e0.30635t
Od tej pory będziemy korzystać z doskonałego, darmowego narzędzia do tworzenia wykresów GeoGebra.
Ustawianie Złotej Spirali za pomocą GeoGebry
Jeśli teraz wykreślimy naszą funkcję na zwykłych prostokątnych osiach współrzędnych w GeoGebrze, otrzymamy następującą krzywą wykładniczą. Zauważmy, że r rośnie w coraz szybszym tempie (staje się bardziej strome) wraz ze wzrostem t.
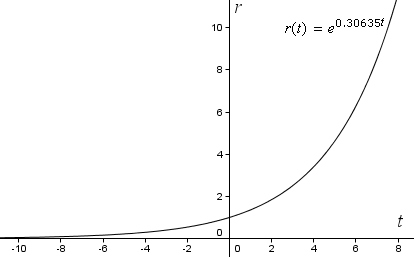
Aby zobaczyć spiralę, musimy wykreślić krzywą przy użyciu współrzędnych biegunowych.
Aby przekształcić postać biegunową (którą mamy) na postać prostokątną (której potrzebujemy do wykresu) w Geogebrze, musimy skonfigurować i wykreślić następującą funkcję:
a(t) = (r(t) cos(t), r(t) sin(t))
Zastąpmy kilka ważnych wartości, aby zobaczyć, co oznacza to wyrażenie. Zaczynając w punkcie t = 0, otrzymujemy punkt początkowy krzywej:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Oznacza to, że zaczynamy 1 jednostkę od początku wzdłuż dodatniej osi x. Punkt początkowy można zobaczyć na poniższym wykresie spirali.
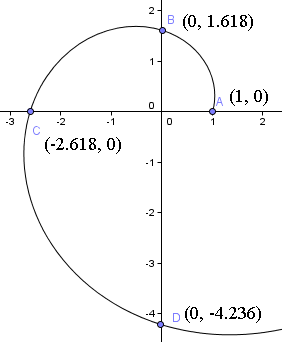
Następnie obracamy się o ćwierć obrotu i znajdujemy w t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1.618×0, 1.618×1)
= (0, 1.618)
Zauważ, że jesteśmy teraz 1.618 jednostek od początku w górę osi y. To znaczy, φ = 1.6180 razy odległość, z której zaczynaliśmy.
Kolejny obrót o ćwierć obrotu doprowadza nas do t = π, gdzie:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2.618×1, -2.618×0)
= (-2.618, 0)
Jesteśmy teraz oddaleni o 2.618 jednostek od początku wzdłuż ujemnej osi x, lub φ = 1.6180 razy odległość od początku, w której byliśmy przy ostatnim ćwierćobrocie.
Uwaga:
φ2 = 2,6180
Możemy obliczyć nasze następne położenie, wzdłuż ujemnej osi y, po prostu mnożąc tę ostatnią wartość przez φ = 1,6180, co daje nam:
φ3 = 4,23606…
Spirala przetnie więc oś y w punkcie (0, -4,236).
Jeszcze jeden ćwierć obrotu doprowadzi nas do φ4 = 6,85410… jednostek wzdłuż dodatniej osi y, czyli (6,854, 0).
Widzimy, że te wartości są poprawne na naszym wykresie spirali powyżej.
Jeśli będziemy kontynuować, otrzymamy spiralę jak poniżej (to 2 pełne obroty, czyli 4π = 720°):
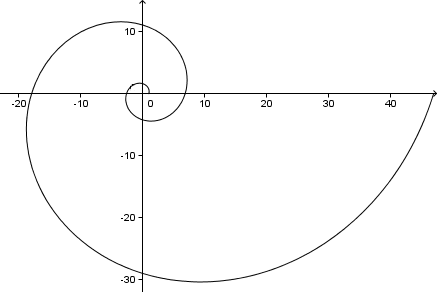
Na marginesie, ponieważ w tym problemie
cot b = 0.30635
to
b = arccot 0.30635 = 1.274 radianów lub około 73°
To jest kąt, jaki nasze ramiona spirali tworzą z linią poprowadzoną ze środka spirali. Możesz zobaczyć na powyższym wykresie, że każde ramię spirali tworzy kąt 73° z osią x (i osią y, lub dowolną linią od środka).
Przybliżenie Złotej Spirali przy użyciu łuków okręgu
Możemy otrzymać spiralę, która wygląda całkiem podobnie do Złotej Spirali, używając łuków okręgów, które zwiększają swój rozmiar o Złoty Stosunek, jak poniżej.
Zaczynamy od kwadratu 1×1 i rysujemy łuk, środek C, przez 2 rogi tak, że boki kwadratu są styczne do łuku (czyli dotykają tylko raz).
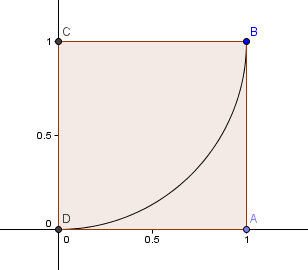
Następnie umieszczamy kwadrat o długości boku φ = 1.6180 nad naszym pierwszym kwadratem i konstruujemy kolejny łuk kołowy, środek E, jak poprzednio:
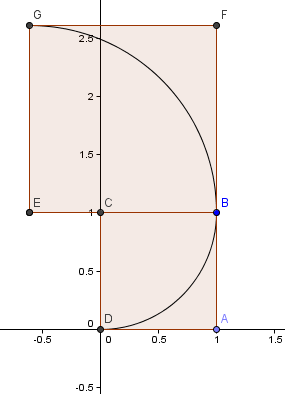
Nasz następny kwadrat idzie po lewej stronie i ma bok φ2 = 2.6180 = 1 + φ.
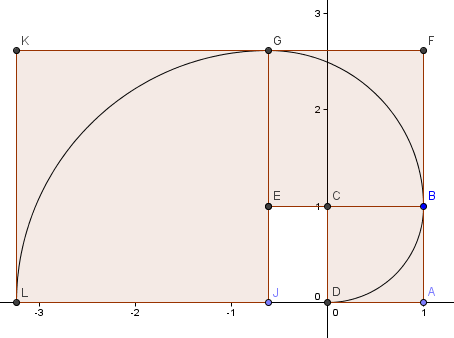
Kontynuujemy wzór (przeszliśmy jeszcze jedno pełne okrążenie) i otrzymujemy spiralę, która wygląda całkiem podobnie do naszej Złotej Spirali sprzed lat.
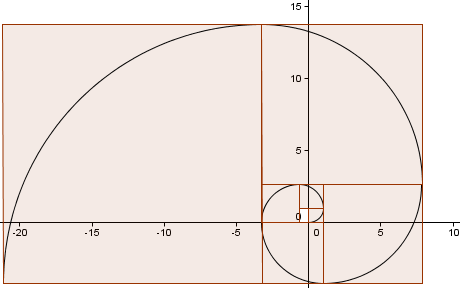
Jak bliskie jest nasze przybliżenie?
W artykule w Wikipedii na temat Złotej Spirali znajduje się obrazek, który twierdzi, że powyższa spirala i Złota Spirala mają bardzo zbliżony kształt.
Oto ten obraz:
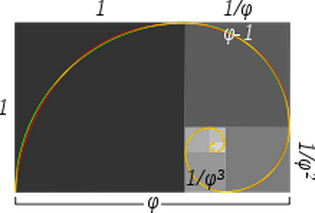
Podpis do obrazu mówi:
Przybliżone i prawdziwe złote spirale: zielona spirala jest zrobiona z ćwierćokręgów stycznych do wnętrza każdego kwadratu, podczas gdy czerwona spirala jest złotą spiralą, specjalnym rodzajem spirali logarytmicznej. Nachodzące na siebie fragmenty są żółte. Długość boku większego kwadratu do następnego mniejszego kwadratu jest w złotej proporcji.
Czy możemy to odtworzyć ?
Na poniższym obrazku, czerwona krzywa jest pierwszą częścią Złotej Spirali, którą skonstruowaliśmy powyżej, podczas gdy zielona krzywa jest oparta na przybliżeniu ćwierćobrotu, nad którym właśnie pracowaliśmy.
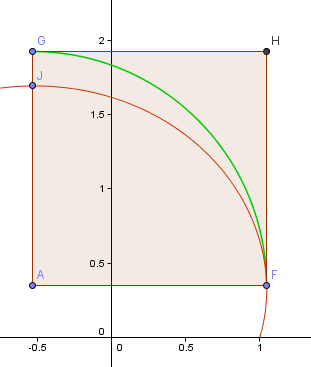
Punkt F jest „najbardziej prawym” punktem na spirali, który będzie moim punktem początkowym dla ćwierćobrotu łuku. Punkt J jest najwyższym punktem tej części spirali.
Punkt A jest punktem przecięcia linii poziomej i pionowej przechodzących odpowiednio przez F i J i to będzie środek mojego łuku.
Teraz, łuk GF nie jest wcale blisko związanej części spirali FJ.
Zróbmy kolejny krok i zobaczmy, czy następna część jest lepsza.
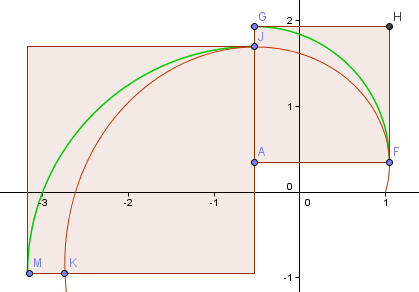
Jak widać, jest gorzej (zgodnie z oczekiwaniami, ponieważ oddaliliśmy się bardziej od początku i ramię spirali staje się większe).
Jasne, to nigdy nie będzie działać.
Jednakże w mojej wcześniejszej Złotej Spirali używałem:
r(t) = e0.30635t
Stała a, miała wartość 1.
Jeśli chcemy, aby nasze łuki aproksymujące dobrze pasowały do rzeczywistej Złotej Spirali, musimy użyć wartości (prawdopodobnie nie jest to zaskakujące)
a = φ = 1.618103399…
Daje nam to następujące krzywe, podobne do wykresu w Wikipedii.
Czerwona krzywa to Złota Spirala,
r(t) = 1.618013 e0.30635t
Zielona krzywa to zbiór łuków kołowych.
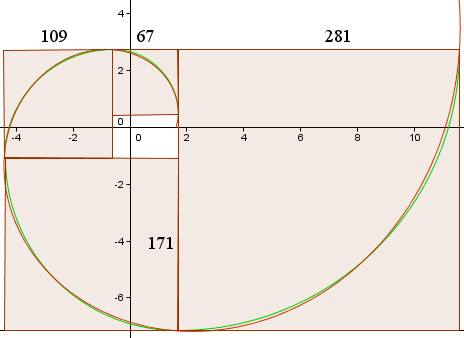
Długości boków kwadratów (w pikselach) są pokazane i widzimy, że są one w przybliżeniu w stosunku 1.618013…
Złota spirala w mediach
Z Wolfram’s Mathworld:
W odcinku 4 sezonu „Masterpiece” (2008) dramatu kryminalnego CBS-TV „Criminal Minds”, agenci Jednostki Analizy Behawioralnej FBI są konfrontowani z seryjnym mordercą, który używa sekwencji liczb Fibonacciego, aby określić liczbę ofiar dla każdego ze swoich epizodów zabijania. W tym odcinku postać dr Reid zauważa również, że miejsca zabójstw leżą na wykresie złotej spirali, a udanie się do środka spirali pozwala Reidowi określić lokalizację bazy operacyjnej zabójcy.
Tutaj więcej ciekawych informacji z Wolfram’s Mathworld:
Spirala logarytmiczna
Dla geeków – projektowanie z wykorzystaniem Złotej Spirali
Wiele osób uważa, że projekty wykorzystujące Złoty Stosunek i Złotą Spiralę są przyjemne dla oka.
Nawet Twitter niedawno przeprojektował swoją stronę główną z wykorzystaniem Złotej Spirali.
Tutaj jest świetny artykuł faceta, który stworzył złotą spiralę bez obrazów. (Głównie dla tych, którzy interesują się projektowaniem stron internetowych)
Złota spirala bez obrazów – przy użyciu CSS i jQuery
Jak sugeruje w artykule, trąba słonia jest również bliska Złotej Spirali.

Pień słonia – prawie Złota Spirala
Podsumowanie
Złota Spirala jest interesującym tematem – takim, którym warto się zająć nie tylko ze względu na przyjemne projekty, ale także ciekawą matematykę stojącą za nimi.
Mam nadzieję, że to pomoże odpowiedzieć na twoje pytanie, Pehr!