Pressão indica a força normal por unidade de área em um determinado ponto atuando em um determinado plano. Como não há tensão de ruptura presente num fluido em repouso – a pressão num fluido é independente da direcção.
Para fluidos – líquidos ou gases – em repouso o gradiente de pressão na direcção vertical depende apenas do peso específico do fluido.
Como a pressão muda com a elevação de um fluido pode ser expressa como
Δp = – γ Δh (1)
where
Δp = variação de pressão (Pa, psi)
Δh = mudança de altura (m, in)
γ = peso específico do fluido (N/m3, lb/ft3)
O gradiente de pressão no sentido vertical é negativo – a pressão diminui para cima.
Peso específico
Peso específico de um fluido pode ser expresso como:
γ = ρ g (2)
where
ρ = densidade do fluido (kg/m3, lesmas/ft3)
>
g = aceleração da gravidade (9.81 m/s2, 32,174 pés/s2)
Em geral o peso específico – γ – é constante para fluidos. Para os gases o peso específico – γ – varia com a elevação (e compressão).
A pressão exercida por um fluido estático depende apenas de
- a profundidade do fluido
- a densidade do fluido
- a aceleração da gravidade
Pressão estática num fluido
Para um fluido incompressível – como um líquido – a diferença de pressão entre duas elevações pode ser expressa como:
Δp = p2 – p1
= – γ (h2 – h1) (3)
>
where
p2 = pressão no nível 2 (Pa, psi)
p1 = pressão no nível 1 (Pa, psi)
h2 = nível 2 (m, ft)
h1 = nível 1 (m, ft)
(3) pode ser transformado em:
Δp = p1 – p2
= γ (h2 – h1) (4)
ou
p1 – p2 = γ Δh (5)
> onde
Δh = h2 – h1 = diferença de elevação – o dept. para baixo do local h2 para h1 (m, ft)
ou
p1 = γ Δh + p2 (6)
Exemplo – Pressão num Fluido
A pressão absoluta à profundidade da água de 10 m pode ser calculada como:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 ou Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
> onde
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = pressão ao nível da superfície = pressão atmosférica = 101,3 kPa
A pressão manométrica pode ser calculada ajustando p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
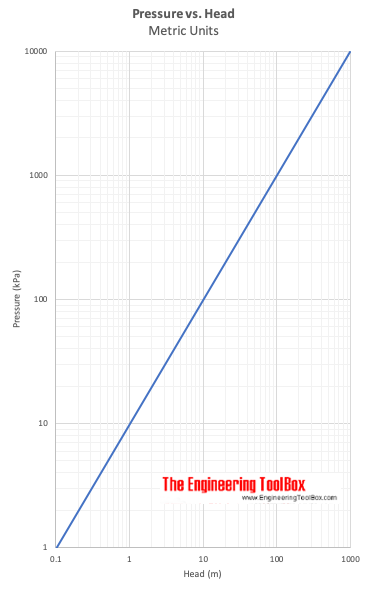
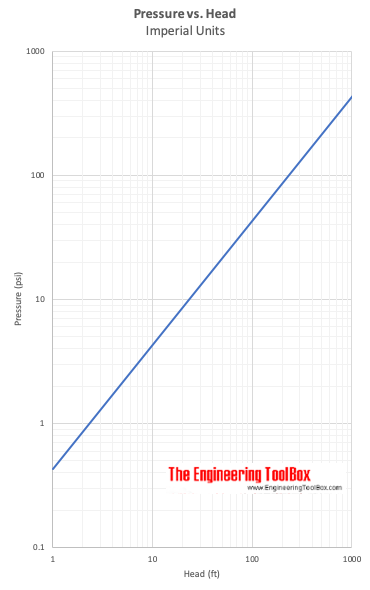
Pressão vs. cabeça
(6) pode ser transformada para:
Δh = (p2 – p1) / γ (7)
Δh cabeça expressa – a diferença de altura de uma coluna de fluido de peso específico – γ – necessária para dar uma diferença de pressão Δp = p2 – p1.
Exemplo – Pressão vs. cabeça
Uma diferença de pressão de 5 psi (lbf/in2) é equivalente à cabeça em água
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11.6 ft de água
ou cabeça em Mercúrio
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0.85 ft de mercúrio
O peso específico da água é 62.4 (lb/ft3) e o peso específico de mercúrio é 847 (lb/ft3).
- Velocidade – Pressão Dinâmica vs. Cabeça