Analiza amortizată este folosită pentru algoritmi care au operații costisitoare care au loc doar rareori.

Analiza complexității amortizate este cel mai frecvent folosită cu structuri de date care au o stare care persistă între operații.Ideea de bază este că o operație costisitoare poate modifica starea astfel încât cel mai rău caz nu se poate repeta pentru o perioadă lungă de timp, amortizându-și astfel costul.
Să fie T1, T2, …, Tk complexitățile unei secvențe de operații asupra unei structuri de date. Complexitatea amortizată a unei singure operații din această secvență este(T1 + T2 + …+ Tk) / k.
Exemplu: un tablou dinamic
Într-un tablou dinamic, elementele sunt stocate la începutul unui tablou fix subiacent, iar pozițiile rămase sunt nefolosite.
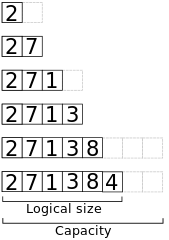
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Iată o vedere a memoriei la adăugarea elementelor 2, 7, 1, 3, 8, 4 la un tablou inițial gol cu capacitatea 2.
Timp în cel mai defavorabil caz
Complexitatea de timp în cel mai defavorabil caz pentru adăugarea unui element la un tablou de lungime n, folosind acest algoritm, este Θ(n).Dacă tabloul este plin, algoritmul alocă un nou tablou de lungime 2n,și apoi copiază elementele din vechiul tablou în cel nou.
Celebrul acest rezultat este excesiv de pesimist.Următoarele n operații de adăugare vor fi mult mai puțin costisitoare -fiecare dintre ele se va executa în timp constant, deoarece tabloul nou alocat are loc pentru toate elementele noi.
Timp amortizat
O analiză a timpului amortizat oferă o înțelegere mult mai bună a algoritmului.
Considerăm o secvență de n operații de adăugare,în care începem cu un tablou de lungime 1. O analiză atentă aratăcă timpul total al acestor operații este de numai Θ(n).
- Vor fi în total n operații de atribuire și incrementare în timp constant.
- Redimensionarea va avea loc numai la operațiile 1, 2, 4, …, 2k, pentru un total de 1 + 2 + 4 + …+ …+ 2k = 2-2k – 1 operații de copiere a elementelor în timp constant. Deoarece 2k ≤ n, aceasta este cel mult 2n – 1.
În consecință, complexitatea în timp amortizată pentru o singură operație de anexare este Θ(1).
Mai multe despre analiza algoritmului

Complexitatea în timp: Numărați-vă pașii

Notația Big O
.