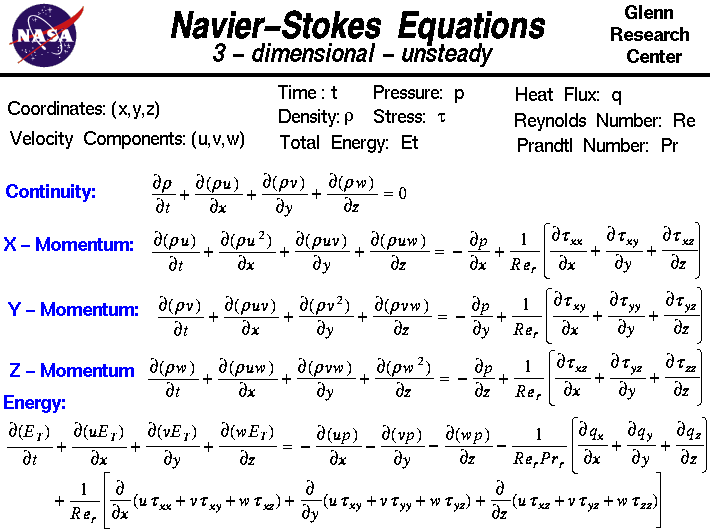
În acest diapozitiv prezentăm forma nestaționară tridimensională a ecuațiilor Navier-Stokes.Aceste ecuații descriu modul în care sunt legate viteza, presiunea, temperatura și densitatea unui fluid în mișcare.Ecuațiile au fost derivate independent de G.G. Stokes, în Anglia, și M. Navier, în Franța, la începutul anilor 1800.Ecuațiile sunt extensii ale ecuațiilor lui Euler și includ efectele vâscozității asupra curgerii.Aceste ecuații sunt foarte complexe, însă studenții de la licență în inginerie sunt învățați cum să le deducă printr-un proces foarte asemănător cu derivarea pe care o prezentăm pe pagina web privind conservarea momentului.
Ecuațiile sunt un set de ecuații diferențiale cuplate și ar putea, în teorie, să fie rezolvate pentru o anumită problemă de curgere folosind metode de calcul.Dar, în practică, aceste ecuații sunt prea dificile pentru a fi rezolvate analitic.În trecut, inginerii făceau alte aproximări și simplificări ale setului de ecuații până când obțineau un grup de ecuații pe care le puteau rezolva.Recent, calculatoarele de mare viteză au fost folosite pentru a rezolva aproximările ecuațiilor folosind o varietate de tehnici cum ar fi diferențele finite, volumul finit, elementele finite și metodele spectrale.Acest domeniu de studiu se numește Computational Fluid Dynamics sau CFD.
Ecuațiile Navier-Stokes constau dintr-o ecuație de continuitate în funcție de timp pentru conservarea masei, trei ecuații de conservare a momentului în funcție de timp și o ecuație de conservare a energiei în funcție de timp.Există patru variabile independente în problemă, coordonatele spațiale x, y și z ale unui domeniu oarecare și timpul t. Există șase variabile dependente: presiunea p, densitatea r și temperatura T (care se regăsește în ecuația energiei prin intermediul energiei totale Et) și trei componente ale vectorului de viteză: componenta u este în direcția x, componenta v este în direcția y și componenta w este în direcția z. Toate variabilele dependente sunt funcții ale tuturor celor patru variabile independente.Ecuațiile diferențiale sunt, prin urmare, ecuații diferențiale parțiale și nu ecuațiile diferențiale ordinare pe care le studiați la începutul cursului de calcul.
Vă veți observa că simbolul diferențial este diferit de simbolul obișnuit „d /dt” sau „d /dx” pe care îl vedeți pentru ecuațiile diferențiale ordinare. Simbolul”
” esteeste folosit pentru a indica derivatele parțiale.Simbolul indică faptul că trebuie să ținem toate variabilele independente fixe, cu excepția variabilei de lângă simbol, atunci când calculăm o derivată. Setul de ecuații este:
Continuitate: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Moment: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Moment: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Moment: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energie: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
unde Re este numărul lui Reynoldscare este un parametru de similaritate care reprezintă raportul dintre scalarea inerției curgerii și forțele vâscoase din curgere. Variabilele q sunt componentele fluxului termic, iar Pr este numărul Prandtl, care este un parametru de similitudine care reprezintă raportul dintre tensiunile vâscoase și tensiunile termice.Variabilele tau sunt componentele tensorului de tensiuni.Un tensor este generat atunci când se înmulțesc doi vectori într-un anumit mod. Vectorul nostru de viteză are trei componente; tensorul de tensiuni are nouă componente. Fiecare componentă a tensorului de tensiuni este ea însăși o derivată a doua a componentelor vitezei.
Termenii din partea stângă a ecuațiilor momentului se numesc termenii de convecție ai ecuațiilor.Convecția este un proces fizic care are loc într-un flux de gaz în care o anumită proprietate este transportată prin mișcarea ordonată a fluxului.Termenii din partea dreaptă a ecuațiilor momentului care sunt înmulțiți cu numărul Reynolds invers se numesc termeni de difuzie.Difuzia este un proces fizic care are loc într-un flux de gaz în care o anumită proprietate este transportată prin mișcarea aleatorie a moleculelor de gaz.Difuzia este legată de tensorul de tensiune și de vâscozitatea gazului. Ecuațiile lui Euler conțin doar termenii de convecție din ecuațiile Navier-Stokes și, prin urmare, nu pot modela straturile limită. Există o simplificare specială a ecuațiilor Navier-Stokesexistă o simplificare specială a ecuațiilor Navier-Stokese care descriu curgerile stratului limită.
Rețineți că toate variabilele dependente apar în fiecare ecuație.Pentru a rezolva o problemă de curgere, trebuie să rezolvați toate cele cinci ecuații simultan; de aceea numim acest sistem un sistem cuplat de ecuații.Există de fapt alte câteva ecuații care sunt necesare pentru a rezolva acest sistem. Noi prezentăm doar cinci ecuații pentru șase necunoscute. O ecuație de starerelaționează presiunea, temperatura și densitatea gazului.Și trebuie să specificăm toți termenii tensorului de tensiuni.În CFD, termenii tensorului de tensiuni sunt adesea aproximați de un model de turbulențe.
Activități:
Vizite ghidate
Navigație ..
Pagina de start a ghidului pentru începători