- Obiective de învățare
- Rețele
- Exemplu 1
- Exemplul 2
- Exerciții de recapitulare
- Răspunsuri
- Prisme
- Suprafața unei prisme folosind rețelele
- Exemplul 3
- Exerciții de recapitulare
- Răspunsuri
- Cilindri
- Arie de suprafață a unui cilindru folosind plase
- Exemplul 4
- Suprafața unui cilindru folosind o formulă
- Exemplu 5
- Exemplul 6
- Exemplul 7
- Sfere
- Arie de suprafață a unei sfere
- Exemplu 8
- Exemplul 9
- Exerciții de recapitulare
- Răspunsuri
Obiective de învățare
- Înțelegeți rețelele.
- Utilizați rețelele pentru a reprezenta prisme.
- Căutați aria suprafeței unei prisme.
- Căutați aria suprafeței cilindrilor.
- Căutați aria suprafeței unei sfere.
Rețele
O ultimă modalitate de a reprezenta un solid este de a folosi o rețea. Dacă decupați o plasă, o puteți plia într-un model al unei figuri. Rețelele pot fi, de asemenea, folosite pentru a analiza un singur solid. Iată un exemplu de plasă pentru un cub.
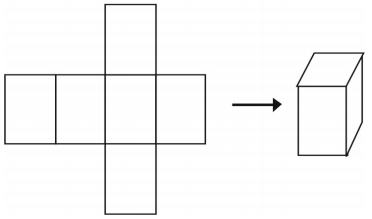
Există mai multe moduri de a face o plasă pentru o singură figură.
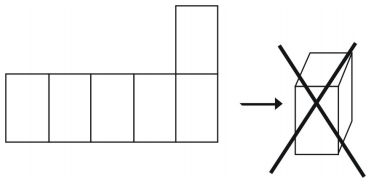
Cu toate acestea, nu toate aranjamentele vor crea un cub.
Exemplu 1
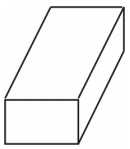
Ce fel de figură creează plasa? Desenați figura.
Rețeaua creează o prismă dreptunghiulară în formă de cutie, așa cum se arată mai jos.
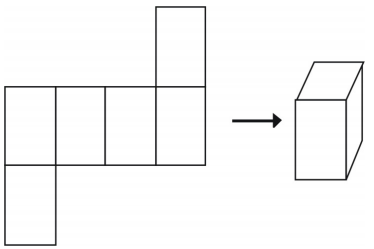
Exemplul 2
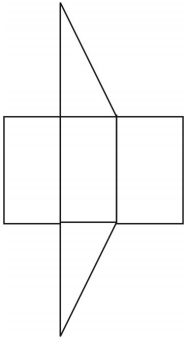
Ce fel de plasă puteți desena pentru a reprezenta figura prezentată? Desenați plasa.
Este prezentată o plasă pentru prismă. Sunt posibile și alte plase.
Exerciții de recapitulare
Desenați o plasă pentru fiecare dintre următoarele:
Răspunsuri
Prisme
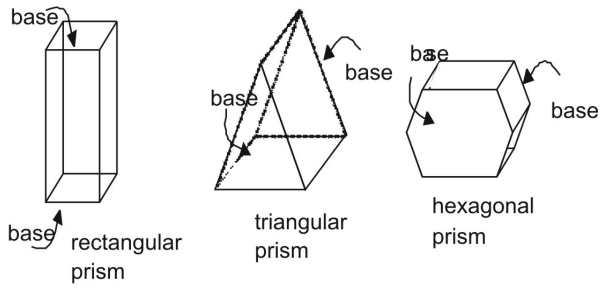
O prismă este o figură tridimensională cu o pereche de capete paralele și congruente, sau baze. Laturile unei prisme sunt paralelograme. Prismele se identifică prin bazele lor.
Suprafața unei prisme folosind rețelele
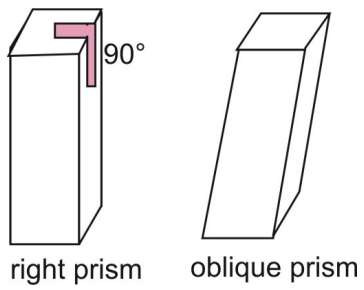
Prizmele de mai sus sunt prisme drepte. Într-o prismă dreaptă, laturile laterale sunt perpendiculare pe bazele prismei. Comparați o prismă dreaptă cu o prismă oblică, în care laturile și bazele nu sunt perpendiculare.
Două postulate care se aplică ariei sunt postulatul de congruență a ariei și postulatul de adunare a ariei.
Puteți folosi o plasă și postulatul adunării ariilor pentru a găsi aria suprafeței unei prisme drepte.
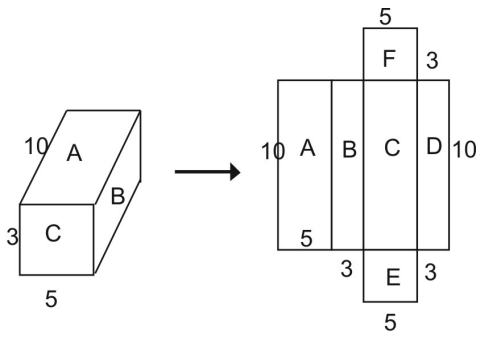
Din plasă, puteți vedea că suprafața întregii prisme este egală cu suma figurilor care alcătuiesc plasa:
Suprafața totală = aria A + aria B + aria C + aria D + aria E + aria F
Utilizând formula pentru aria unui dreptunghi, puteți vedea că aria dreptunghiului A este:
:
A = l – l
A = 10 – 5 = 50 unități pătrate
În mod similar, ariile celorlalte dreptunghiuri se introduc din nou în ecuația de mai sus.
Suprafața totală = aria A + aria B + aria C + aria D + aria E + aria F
Suprafața totală = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 3) + (5 – 3)
Suprafața totală = 50 + 30 + 50 + 30 + 30 + 15 + 15 + 15
Suprafața totală = 190 unități pătrate
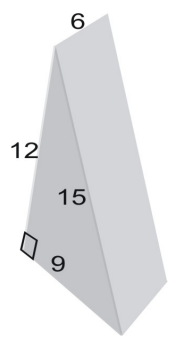
Exemplul 3
Utilizați o plasă pentru a afla suprafața prismei.
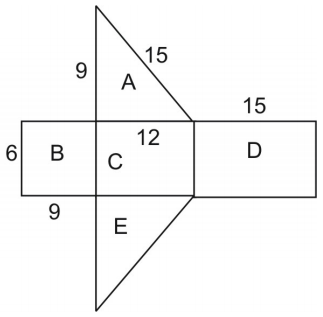
Aria plasei este egală cu aria suprafeței figurii. Pentru a afla aria triunghiului, folosim formula:
\displaystyle{A}=\frac{1}{2}hb\\ unde h este înălțimea triunghiului și b este baza acestuia.
Rețineți că triunghiurile A și E sunt congruente, astfel încât putem înmulți aria triunghiului A cu 2.
\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\
\displaystyle\text{area }=2(\text{area }A)+\text{area }. }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, suprafața este de 324 de unități pătrate.
Exerciții de recapitulare
Pentru fiecare dintre următoarele găsiți suprafața sunt a folosind metoda rețelelor și perimetrul


- Baza unei prisme este un triunghi dreptunghic al cărui catete sunt 3 și 4 și arată că înălțimea este 20. Care este aria totală a prismei?
- O prismă hexagonală dreaptă are o înălțime de 24 de centimetri și are baze care sunt hexagoane regulate care măsoară 8 centimetri pe o latură. Care este suprafața totală?
- Care este volumul prismei din problema nr. 4?
În următoarele întrebări, un hambar are forma unei prisme pentagonale cu dimensiunile indicate în picioare:

- Câți metri pătrați (excluzând acoperișul) sunt pe suprafața hambarului care urmează să fie vopsit?
- Dacă un galon de vopsea acoperă 250 de picioare pătrate, câți galoni de vopsea sunt necesari pentru a vopsi hambarul?
- O cutie de carton este un cub perfect cu o margine care măsoară 17 inci. Câți metri cubi poate să conțină?
- O piscină are 16 picioare lățime, 32 picioare lungime și o adâncime uniformă de 4 picioare. Câți metri cubi de apă poate conține?
- O cutie de cereale are o lungime de 25 cm, o lățime de 9 cm și o înălțime de 30 cm. Câte cereale poate să conțină?
Răspunsuri
Rețele și perimetru:
- 40.5 in2
- 838 cm2
- 252 unități pătrate
- 1484.6 unități pătrate
- 3990,7 inci cubice
Garnița:
- 2450 de picioare pătrate
- 10 galoane de vopsea
- 2,85 de picioare cubice (fiți atenți aici. Unitățile din problemă sunt date în inci, dar întrebarea cere picioare.)
- 2048 picioare cubice
- 6750 cm3
Cilindri
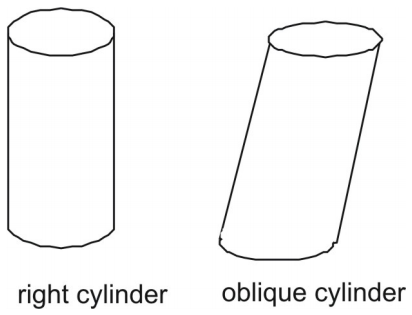
Un cilindru este o figură tridimensională cu o pereche de capete circulare paralele și congruente, sau baze. Un cilindru are o singură latură curbată care formează un dreptunghi atunci când este așezat în plan.
Ca și în cazul prismelor, cilindrii pot fi drepți sau oblici. Latura unui cilindru drept este perpendiculară pe bazele sale circulare. Latura unui cilindru oblic nu este perpendiculară pe bazele sale.
Arie de suprafață a unui cilindru folosind plase
Puteți deconstrui un cilindru într-o plasă.
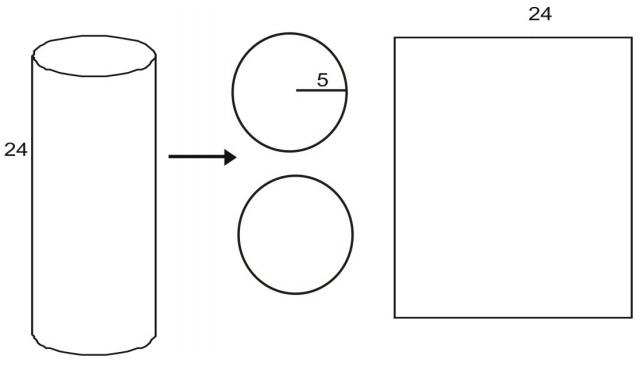
Ariza fiecărei baze este dată de aria unui cerc:
A=\pi{r}^2\\
A=\pi(5)^2\\
A=25\pi\\
A\aprox(25)(3,14)=78,5\\
Ariza suprafeței laterale rectangulare L este dată de produsul dintre o lățime și o înălțime. Înălțimea este dată ca fiind 24. Se poate observa că lățimea ariei este egală cu circumferința bazei circulare.
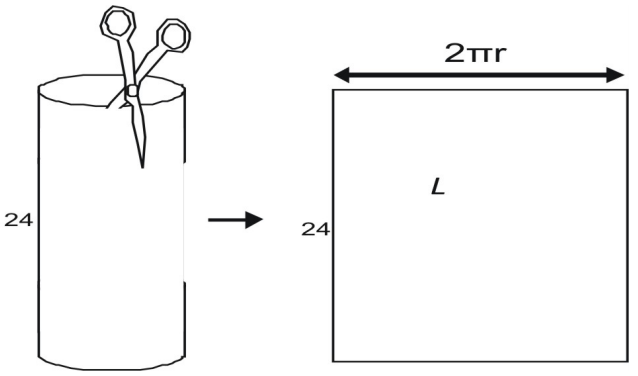
Pentru a afla lățimea, imaginați-vă că desfaceți cu o foarfecă un cilindru asemănător unei cutii de conserve. Când tăiați aria laterală, vedeți că aceasta este egală cu circumferința vârfului cutiei. Circumferința unui cerc este dată de C = 2πr, iar aria laterală, L, este
L=2{\pi}rh\\\
L=2{\pi}(5)(24)\\
L=240\pi\\
L\aprox(240)(3.14)=753,6\\
Acum putem afla aria întregului cilindru folosind A = (aria celor două baze) + (aria laturii laterale).
A=2(75.36)+753.6\\
A=904.32\\
Vezi că formula pe care am folosit-o pentru a găsi aria suprafeței totale poate fi folosită pentru orice cilindru drept.
Exemplul 4
Utilizați o plasă pentru a afla aria suprafeței cilindrului.
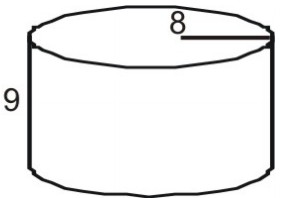
În primul rând, desenați și etichetați o plasă pentru figură.
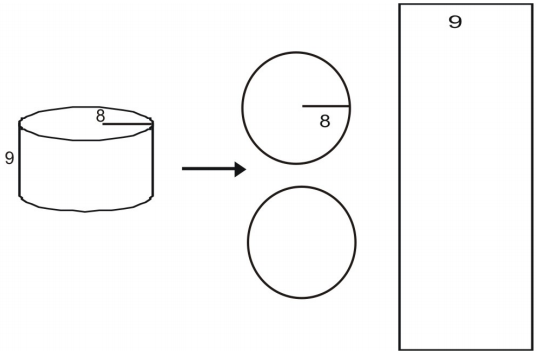
Calculați aria fiecărei baze.
A=\pi{r}^2\\
A=\pi(8)^2\\
A=64\pi\\
A\aprox(64)(3.14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452,16\\
Găsește aria întregului cilindru.
A=2(200,96)+452,16\
A=854.08\\
Acum, suprafața totală este de aproximativ 854,08 unități pătrate
Suprafața unui cilindru folosind o formulă
Ai văzut cum să folosești plase pentru a afla suprafața totală a unui cilindru. Postulatul poate fi descompus pentru a crea o formulă generală pentru toți cilindrii drepți.
A = 2B + L

Observați că baza, B, a oricărui cilindru este: B = πr2
Ariza laterală, L, pentru orice cilindru este: B = πr2
Ariza laterală, L, pentru orice cilindru este:
L=\text{lățimea suprafeței laterale}\cdot\text{înălțimea cilindrului}\\
L=\text{circumferința bazei}\cdot\text{înălțimea cilindrului}\\\
L=2\pi{r}\cdot{h}\\
Punând cele două ecuații împreună obținem:
Factorizarea lui a din ecuație dă:
Suprafața unui cilindru drept: Un cilindru drept cu raza r și înălțimea h poate fi exprimat astfel:
A = 2πr2 + 2πrh
sau:
A = 2πr(r + h)
Puteți utiliza formulele pentru a afla aria oricărui cilindru drept.
Exemplu 5
Utilizați formula pentru a afla aria suprafeței cilindrului.
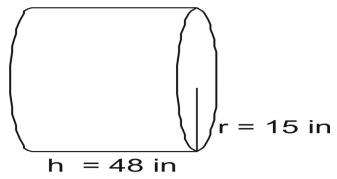
Scrieți formula, înlocuiți valorile și rezolvați.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ inci pătrați}\\\
Exemplul 6
Căutați aria suprafeței cilindrului.
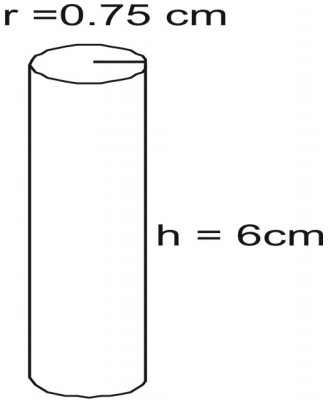
Scrieți formula, înlocuiți valorile și rezolvați.
A=2\pi{r}(r+h)\
A=2(3,14)(0,75)\
A=31.7925\text{ inci pătrați}\\
Exemplul 7
Găsește înălțimea unui cilindru care are raza de 4 cm și suprafața de 226,08 cm pătrați.
Scrieți formula cu informațiile date și rezolvați pentru h.
A=2\pi{r}(r+h)\
226.08=2(3.14)(4)\
226.08=25.12\
226.08=100.48+25.12h\
5=h\
Sfere
Osfera este o figură tridimensională care are forma unei bile.

Sferele pot fi caracterizate în trei moduri.
- O sferă este ansamblul tuturor punctelor care se află la o distanță fixă r de un singur punct central O.
- O sferă este suprafața care rezultă atunci când un cerc este rotit în jurul oricăruia dintre diametrele sale.
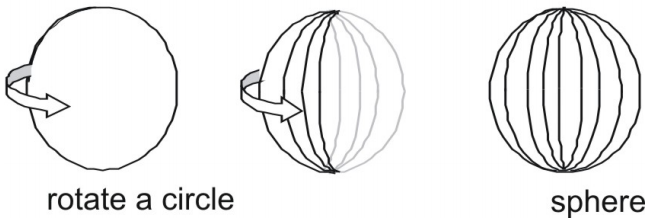
Arie de suprafață a unei sfere
Puteți deduce formula pentru aria de suprafață a unei sfere luând măsurători ale sferelor și cilindrilor. Aici arătăm o sferă cu raza de 3 și un cilindru drept cu raza și înălțimea de 3 și exprimăm aria în termeni de π.
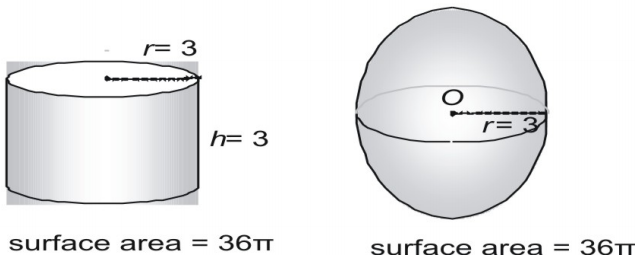
Încercați acum o pereche mai mare, exprimând aria suprafeței în formă zecimală.
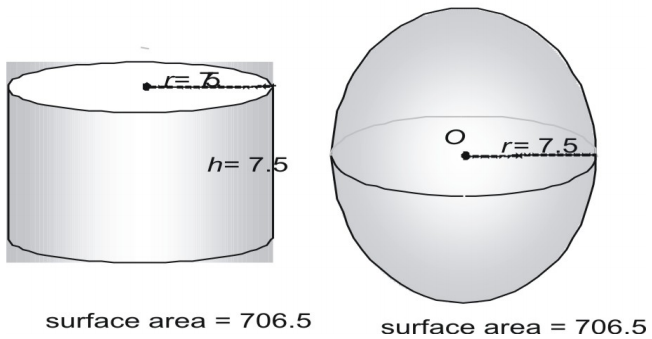
Vezi o a treia pereche.
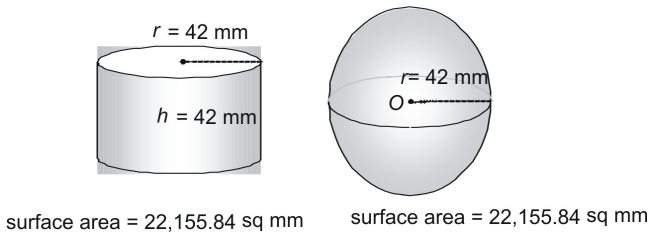
Este o coincidență faptul că o sferă și un cilindru a cărui rază și înălțime sunt egale cu raza sferei au exact aceeași suprafață? Nici vorbă de așa ceva! De fapt, grecii antici au folosit o metodă care a arătat că următoarea formulă poate fi folosită pentru a afla suprafața oricărei sfere (sau a oricărui cilindru în care ).
Exemplu 8
Căutați suprafața unei sfere cu raza de 14 picioare.
Utilizați formula.
A=4\pi{r}^2\
A=4\pi(14)^2\\
A=4\pi(196)\
A=784\pi\\
A=2461.76\text{ picioare pătrate folosind }3.14\text{ pentru }\pi\\\
Exemplul 9
Găsește suprafața următoarei figuri în termenii lui π.
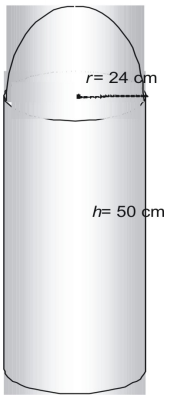
Figura este formată dintr-o jumătate de sferă sau emisferă și un cilindru fără vârf.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half sphere})=2\pi(576)\
A(\text{jumătate de sferă})=1152\pi\text{cm pătrați}\\
Acum găsiți aria cilindrului fără vârf.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, suprafața totală este 1152\pi+2976\pi=4128\pi\\\\
Exerciții de recapitulare
- Căutați raza sferei care are un volum de 335 cm3.
- Determinați suprafața și volumul acestei forme:

- Raza unei sfere este 4. Aflați volumul și suprafața totală a acesteia.
- O sferă are raza de 5. Un cilindru drept, având aceeași rază are același volum. Găsiți înălțimea și suprafața totală a cilindrului.
- Sferă: volum = 296 cm3. Găsiți Diametrul.
- Sferă: suprafața este de 179 in2. Aflați raza.
- Bilele de tenis cu diametrul de 3,5 inci se vând în cutii de trei. Cutia este un cilindru. Să presupunem că bilele ating cutia pe laturi, sus și jos. Care este volumul spațiului neocupat de mingile de tenis?
- O sferă are suprafața de 36π in2. Găsiți volumul său.
- O lopată gigantică, acționată de o macara, are forma unei emisfere cu raza = 21 inci. Lingura este umplută cu oțel fierbinte topit. Când oțelul este turnat într-un rezervor de depozitare cilindric care are raza de 28 inch, oțelul topit se va ridica la o înălțime de câți inch?
Răspunsuri
Rețineți că aceste probleme folosesc π și nu 3.14.
- 1. Raza = 4,31 cm
- Suprafața = 706,86 cm2
Volumul = 1767,15 cm3 - Volumul = 268,08 unități3
Suprafața = 201,06 unități2 - Înălțimea = 20/3 unități suprafața totală = 366,52 unități2
- Diametrul = 8,27cm
- Raza = 3.77 inci
- Volumul cilindrului = 32,16π in3 volumul bilelor de tenis = 21,44π in3
Volumul spațiului neocupat de bilele de tenis = 33,68 in3 - Volumul = 113,10 in3
- Înălțimea oțelului topit în cilindru va fi de 7,88 inci
.



