Un strat limită este un strat subțire de fluid vâscos în apropierea suprafeței solide a unui perete în contact cu un curent în mișcare, în care (în cadrul grosimii sale δ) viteza de curgere variază de la zero la perete (unde curgerea „se lipește” de perete din cauza vâscozității sale) până la Ue la limită, care corespunde aproximativ (cu o eroare de 1%) vitezei curentului liber (a se vedea figura 1). Strict vorbind, valoarea lui δ este o valoare arbitrară, deoarece forța de frecare, care depinde de interacțiunea moleculară dintre fluid și corpul solid, scade odată cu distanța față de perete și devine egală cu zero la infinit.
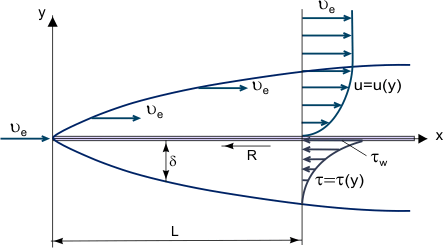
Figura 1. Creșterea unui strat limită pe o placă plană.
Conceptul fundamental al stratului limită a fost sugerat de L. Prandtl (1904), acesta definește stratul limită ca fiind un strat de fluid care se dezvoltă în curgeri cu numere Reynolds Re foarte mari, adică cu o vâscozitate relativ scăzută în comparație cu forțele de inerție. Acest lucru se observă atunci când corpurile sunt expuse unui curent de aer cu viteză mare sau când corpurile sunt foarte mari, iar viteza curentului de aer este moderată. În acest caz, într-un strat limită relativ subțire, tensiunea de forfecare prin frecare (forța de forfecare vâscoasă): τ = η (unde η este vâscozitatea dinamică; u = u(y) – „profilul” componentei longitudinale a vitezei stratului limită, a se vedea figura 1) poate fi foarte mare; în special, la perete, unde u = 0 și τw = ηw, deși vâscozitatea însăși poate fi destul de mică.
Este posibil să se ignore forțele de frecare din afara stratului limită (în comparație cu forțele de inerție) și, pe baza conceptului lui Prandtl, să se considere două regiuni de curgere: stratul limită unde efectele de frecare sunt mari și miezul curgerii aproape invizibile. Pornind de la premisa că stratul limită este un strat foarte subțire (δ << L, unde L este dimensiunea liniară caracteristică a corpului peste care se produce curgerea sau a canalului care conține curgerea, grosimea acestuia scăzând odată cu creșterea lui Re, figura 1), se poate estima ordinul de mărime al grosimii stratului limită din următoarea relație:
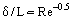
De exemplu, când un avion zboară cu Ue = 400 km/h, grosimea stratului limită la marginea de fugă a aripii cu o coardă de 1 metru (lungimea profilului) este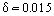
m. Așa cum s-a stabilit experimental, la secțiunea de intrare a corpului se dezvoltă un strat limită laminar. Treptat, sub influența unor factori destabilizatori, stratul limită devine instabil și are loc tranziția stratului limită la un regim de curgere turbulentă. Cercetări experimentale speciale au stabilit existența unei regiuni de tranziție între regimul turbulent și cel laminar. În unele cazuri (de exemplu, la un nivel ridicat de turbulență al curgerii externe), stratul limită devine turbulent imediat în aval de punctul de stagnare al curgerii. În anumite condiții, cum ar fi o cădere severă de presiune, în cazul curgerilor turbulente accelerate are loc un fenomen invers, și anume relaminarizarea curgerii.
În ciuda subțirimii sale relative, stratul limită este foarte important pentru inițierea proceselor de interacțiune dinamică între curgere și corp. Stratul limită determină rezistența aerodinamică și portanța vehiculului zburător, sau pierderea de energie pentru curgerea fluidelor în canale (în acest caz, un strat limită hidrodinamic, deoarece există și un strat limită termic care determină interacțiunea termodinamică a Transferului de căldură).
Calcularea parametrilor stratului limită se bazează pe rezolvarea ecuațiilor obținute din ecuațiile Navier-Stokes pentru mișcarea fluidelor vâscoase, care sunt mai întâi simplificate considerabil ținând cont de subțirimea stratului limită.
Soluția propusă de L. Prandtl este, în esență, primul termen al expansiunii în serie de puteri a ecuației Navier-Stokes, expansiunea în serie fiind realizată pentru puteri ale parametrului adimensional (δ/L). Parametrul mai mic din acest termen este în putere zero, astfel încât ecuația stratului limită este aproximația zero într-o expansiune asimptotică (la Re mare) a ecuației stratului limită (soluție asimptotică).
O transformare a ecuației Navier-Stokes în ecuațiile stratului limită poate fi demonstrată prin derivarea ecuației Prandtl pentru stratul limită laminar într-un curgere incompresibilă bidimensională fără forțe ale corpului.
În acest caz, sistemul de ecuații Navier-Stokes va fi:
După evaluarea ordinului de mărime al unor termeni din Ec. (2) și ignorând termenii mici, sistemul de ecuații Prandtl pentru stratul limită laminar devine:
în care x, y sunt coordonatele longitudinale și laterale (figura 1); v este componenta vitezei de-a lungul axei „y”; p, presiunea; t, timpul; și n vâscozitatea cinematică.
Stratul limită este subțire, iar viteza la marginea sa externă Ue poate fi determinată suficient și precis ca viteză a unui flux de fluid ideal (invizibil) de-a lungul peretelui, calculată până la prima aproximație, fără a lua în considerare acțiunea inversă a stratului limită asupra fluxului extern. Gradientul de presiune longitudinală = (la p(y) = const) din ecuația (3) poate fi descris din ecuația Euler a mișcării unui fluid ideal. Din cele de mai sus, ecuațiile Prandtl în forma lor finită se vor scrie sub forma::
Este un sistem de ecuații parabolice, neliniare cu derivate parțiale de ordinul al doilea care se rezolvă cu condiții inițiale și la limită
Sistemul de ecuații (4) se scrie pentru valorile reale ale componentelor de viteză u și v. Pentru a generaliza ecuațiile obținute pentru curgerea turbulentă, trebuie utilizată relația bine cunoscută între componentele reale, medii și pulsatorii ale parametrilor curgerii turbulente. De exemplu, pentru componentele de viteză există relații care leagă componentele reale u și v, medii ū și
și pulsatorii u’ și v’:
După câteva rearanjări, este posibil să se obțină un alt sistem de ecuații din sistemul (3), în special pentru curgerea constantă:
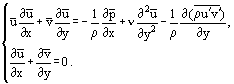
Utilizând următoarea relație pentru tensiunea de forfecare prin frecare în stratul limită:
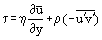
și ținând cont de faptul că în stratul limită laminar u = u’ și
este posibilă rescrierea ecuațiilor Prandtl într-o formă valabilă atât pentru curgerile laminare cât și pentru cele turbulente:
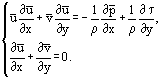
Cele mai simple soluții au fost obținute pentru un strat limită laminar pe o placă plană subțire într-un curgere paralelă bidimensională de fluid incompresibil (figura 1). În acest caz, estimarea ordinului de mărime al termenilor ecuațiilor: x ~ L, y ~ δ, δ ~
permite combinarea variabilelor x și y într-o singură relație
și reducerea soluției Ecuației (8) (la dp/dx = 0) la determinarea dependențelor lui u și v de noul parametru ξ. Pe de altă parte, folosind relațiile bine cunoscute dintre componentele vitezei u, v și funcția de curgere ψ
este posibilă obținerea unei ecuații diferențiale neliniare ordinare de ordinul trei, în locul sistemului de ecuații cu derivate parțiale (8)
Aici, f(ξ) este funcția necunoscută a variabilei ξ: f = ƒ =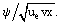
Prima soluție numerică a ecuației. (10) a fost obținută de Blasius (1908) în condiții limită corespunzătoare condițiilor fizice ale stratului limită la y = 0: u = 0, v = 0; la y → ∞; u → Ue (stratul limită Blasius).
Figura 2 compară rezultatele soluției lui Blasius (linie continuă) cu datele experimentale. Folosind aceste date, este posibil să se evalueze grosimea stratului limită vâscos. La ξ 
2,5, (u/Ue 0,99) (figura 2); în consecință, din ecuația (9) se obține:
Figura 2.
Din calculele numerice Blasius ale valorii derivatei a doua a funcției f(ξ) la solicitarea de forfecare prin frecare a peretelui, relația în acest caz este:
Forța de frecare R, care acționează pe ambele părți ale plăcii de lungime L (figura 1), se determină tot din Ecuația. (11):
ca și în cazul coeficientului de frecare pentru plăci plane:
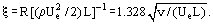
În ciuda faptului că ecuațiile Prandtl sunt mult mai simple decât ecuațiile Navier-Stokes, soluțiile acestora au fost obținute pentru un număr limitat de probleme. Pentru multe probleme practice, nu este necesar să se determine profilurile de viteză în stratul limită, ci doar grosimea și tensiunea de forfecare. Acest tip de informații poate fi obținut prin rezolvarea ecuației integrale a momentului
Relația integrală (12) este valabilă atât pentru stratul limită laminar, cât și pentru cel turbulent.
Funcțiile care nu erau cunoscute a priori, dar care caracterizează distribuția parametrilor fluidului de-a lungul grosimii stratului δ se află sub integrala din ecuația (12). Iar eroarea de calcul a integralei este mai mică decât eroarea funcției integrantă aproximativ presupusă ρu = ρu(y). Acestea creează condiții pentru dezvoltarea unor metode aproximative de calculare a parametrilor stratului limită, care necesită mai puțin timp decât metodele exacte de integrare a ecuațiilor Prandtl. Conceptul fundamental a fost sugerat pentru prima dată de T. von Karman, care a introdus o astfel de grosime arbitrară a stratului δ*
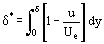
și grosimea de deplasare a momentului δ**
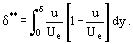
astfel, putem transforma Ecuația (12) pentru stratul limită bidimensional al unui fluid incompresibil în:
Există trei funcții necunoscute în Ecuația (15), și anume, δ* = δ*(x), δ** = δ**(x) și τw = τw(x) .
Soluția unei ecuații diferențiale ordinare precum Ecuația (15) este o ecuație diferențială ordinară. (15) necesită, de obicei, presupunerea (sau reprezentarea) distribuției vitezei (profilul vitezei) de-a lungul grosimii stratului limită în funcție de anumiți parametri caracteristici (parametrii de formă) și necesită, de asemenea, utilizarea unor date empirice despre relația dintre coeficientul de frecare Cf = 2τw/(ρU2e) și grosimea arbitrară a stratului limită (legea frecării).
Se pot da unele explicații fizice certe în ceea ce privește valorile lui δ* și δ**. Funcția integrantă din ecuația (13) conține, după rearanjare, un termen (Ue – u) care caracterizează scăderea vitezei. Integrala din Ecuația (14) poate fi astfel considerată ca o măsură a scăderii debitului prin stratul limită, în comparație cu curgerea perfectă a fluidului la viteza Ue. Pe de altă parte, valoarea lui δ* poate fi considerată ca fiind măsura abaterii de-a lungul unei normale la perete (de-a lungul axei „y”) a liniei de curgere a fluxului exterior sub influența forțelor de frecare. Din această considerație a structurii integrale a ecuației (14), se poate concluziona că δ** caracterizează scăderea impulsului în stratul limită sub influența forțelor de frecare.
Sunt valabile următoarele relații:
unde H este parametrul de formă al profilului de viteză al stratului limită. De exemplu, pentru distribuția liniară u = ky,
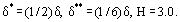
În prezent, așa-numitele teorii semiempirice sunt utilizate pe scară largă pentru prezicerea parametrilor stratului limită turbulent. În acest caz, se presupune că tensiunea totală de frecare τ într-un strat limită turbulent este o sumă
Aici, τT este tensiunea de frecare suplimentară (turbulentă sau Reynolds), în special, într-un curgere incompresibilă
vezi Ecuația. (7).
Această reprezentare este direct legată de sistemul de ecuații de mișcare în stratul limită (6). În stratul limită compresibil, pulsațiile de densitate pot fi considerate ca fiind rezultatul pulsațiilor de temperatură
unde β = (1/T) este coeficientul de expansiune volumetrică.
Pentru determinarea lui τT se folosesc ipoteze semi-empirice suplimentare despre transferul de moment turbulent. De exemplu,
unde ηT este coeficientul dinamic al vâscozității turbulente introdus de J. Boussinesq în 1877.
Pe baza conceptului de similitudine a schimburilor moleculare și turbulente (teoria similitudinii) Prandtl a introdus ipoteza lungimii de amestec (die Mischungsweg). Lungimea de amestecare 1 este drumul pe care un volum finit de fluid („mol”) trece de la un strat de mișcare medie la altul fără a-și schimba impulsul. În conformitate cu această condiție, el a derivat o ecuație care s-a dovedit a fi fundamentală pentru teoria stratului limită:
Pentru regiunea turbulentă a stratului limită al curgerii în apropierea peretelui, L. Prandtl a considerat lungimea 1 proporțională cu y
unde κ este o constantă empirică.
În apropierea peretelui, unde ηT << η, frecarea moleculară vâscoasă este un factor determinant. Grosimea acestei părți a stratului limită δ1, care este cunoscută ca substrat laminar sau vâscos, este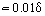
. În afara substratului, valoarea lui ηT crește, ajungând cu câteva ordine de mărime mai mare decât η. În mod corespunzător, în această zonă a stratului limită cunoscută sub numele de miez turbulent τT > 0 = η. Uneori, miezul turbulent este subdivizat în zona tampon, în care frecarea laminară și turbulentă au valoare comparabilă, și zona dezvoltată, în care τT >> τ0. Pentru această regiune, după integrarea ecuației (18) și ținând cont de ecuația (19), se poate obține o expresie pentru profilul logaritmic al vitezei:
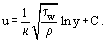
Dacă se folosesc coordonate adimensionale (sau universale).
unde
este așa-numita viteză dinamică (sau viteza de frecare), Ec. (20) poate fi rescrisă în următoarea formă:
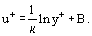
Reprezentarea distribuției vitezei în coordonate universale și modelele matematice pentru coeficientul de vâscozitate turbulentă sunt tratate mai detaliat în secțiunea de curgere turbulentă.
Una dintre versiunile actuale ale teoriei semi-empirice a stratului limită turbulent dezvoltată de S. S. Kutateladze și A. I. Leontiev se bazează pe așa-numita teorie asimptotică a straturilor limită turbulente la Re → ∞ unde grosimea substratului laminar (vâscos) δ1 scade cu o rată mai mare decât δ ca urmare a faptului că (δ1/δ) → 0.
În aceste condiții, se dezvoltă un strat limită turbulent cu „vâscozitate de dispariție”. În acest strat, η → 0, dar nu este egal cu zero și, din acest punct de vedere, stratul diferă de curgerea perfectă a fluidului. Conceptul de lege de frecare relativă, introdus de S. S. Kutateladze și A. I. Leontiev (1990), indică
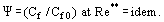
Legea se definește ca fiind raportul dintre coeficientul de frecare Cf pentru condiția considerată și valoarea lui Cf0 pentru condiții „standard” pe o placă plană, impermeabilă, survolată de un flux incompresibil, izoterm, ambii coeficienți fiind obținuți pentru Re** = Ueδ**/ν. Se arată că la Re → ∞; η → 0; și Cf → 0, variația relativă a coeficientului de frecare sub influența unor factori perturbatori cum ar fi gradientul de presiune, compresibilitatea, neizotermia, injecția (aspirația) printr-un perete poros etc., are o valoare finită.
Ecuațiile derivate pentru calcularea valorii lui Ψ au o caracteristică importantă care face ca Ψ să fie independentă de constantele empirice ale turbulenței. În conformitate cu conceptul fundamental al „abordării” integrale, ecuația integrală a momentului se transformă în:
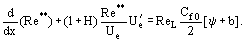
Aici,
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sunt parametrii de permeabilitate pentru cazul în care se injectează un gaz cu densitatea ρw printr-un perete permeabil cu viteza vw. Pentru determinarea funcției Re** = Re**
, este necesar să se calculeze distribuția
În acest scop, se aplică principiul suprapunerii factorilor perturbatori
În ecuația Eq. 24, fiecare multiplicator reprezintă legea de frecare relativă, ținând cont de efectul unuia dintre factori, printre care compresibilitatea ΨM, capul de temperatură (sau entalpie) ΨT, injecția ΨB, gradientul de presiune ΨP și altele.
Conceptele fundamentale ale stratului limită creează condiții pentru explicarea unor fenomene precum separarea curgerii de la suprafață sub influența inerției curgerii, decelerația curgerii vâscoase de către perete și gradientul de presiune adversă care acționează în direcția amonte = 0 sau < 0.
Dacă gradientul de presiune este advers pe locația de la suprafață dintre secțiunile „1-4” (a se vedea figura 3), distribuția vitezei u = u(x,y) în stratul limită se modifică treptat; devenind „mai puțin plină”, scăzând înclinarea în jeturile de fluid care sunt mai aproape de perete și care posedă o cantitate mai mică de energie cinetică (a se vedea formele profilului de viteză din figura 3) care pătrund mult în aval în regiunea de presiune crescută. În unele secțiuni, de exemplu în secțiunea „4”, particulele de fluid care se află pe linia de curgere „a-a” (linia punctată din figura 3) – după ce și-au epuizat complet rezerva de energie cinetică devin decelerate (ua = 0).
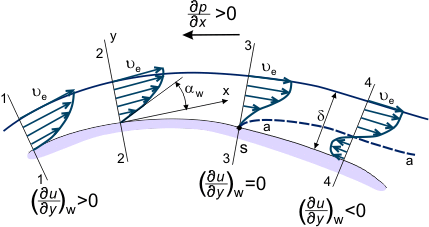
Figura 3. Stratul limită în curgerea peste o suprafață acoperită.
Presiunea statică și valoarea gradientului de presiune nu variază pe grosimea stratului limită. Prin urmare, particulele de fluid care sunt mai aproape de perete decât linia „a-a” și care posedă încă o cantitate mai mică de energie încep să se deplaseze în direcția opusă sub influența gradientului de presiune în secțiunea „4-4” (a se vedea figura 3). Astfel, rezultă relația:
În acest fel, în unele locuri de pe suprafață, profilul vitezei se modifică. Această modificare se caracterizează prin modificarea semnului derivatei w de la pozitiv (secțiunea 2, figura 3) la negativ (secțiunea 4). Desigur, este de asemenea posibil să se definească secțiunea în care w = 0 (secțiunea 3, figura 3). Aceasta este denumită secțiunea de separare a stratului limită (punctul „S” de pe suprafața acestei secțiuni este punctul de separare). Aceasta se caracterizează prin dezvoltarea unei zone de curgere inversă – curgerea în jurul corpului nu mai este netedă, stratul limită devine considerabil mai gros, iar liniile de curgere exterioare ale fluxului se abat de la suprafața corpului învecinat. În aval de punctul de separare, distribuția presiunii statice de-a lungul grosimii stratului nu este constantă, iar distribuția presiunii statice de-a lungul suprafeței nu corespunde distribuției presiunii în curgerea exterioară, invizibilă.
Separația este urmată de dezvoltarea unor zone de curgere inversă și de vârtejuri, în care energia cinetică furnizată de curgerea exterioară se transformă în căldură sub influența forțelor de frecare. Separarea fluxului, însoțită de disiparea energiei în zonele de turbionare a fluxului invers, are ca rezultat efecte nedorite, cum ar fi creșterea rezistenței la înaintare a vehiculelor zburătoare sau pierderile hidraulice în canale.
Pe de altă parte, fluxurile separate sunt utilizate în diferite dispozitive pentru amestecarea intensivă a fluidului (de exemplu, pentru a îmbunătăți amestecul de combustibil și aer în camerele de combustie ale motoarelor). Atunci când fluidele vâscoase curg în canale cu secțiune transversală variabilă (gradient de presiune alternativ), zona de separare poate fi locală dacă secțiunea difuzorului este urmată de secțiunea confuzorului, unde fluxul separat se va reatașa din nou la suprafață (a se vedea figura 4a). Atunci când curgerea se separă de marginea de fugă a corpului (de exemplu, de marginea de fugă a aripii), se formează așa-numitul wake prin „legarea” straturilor limită (a se vedea figura 4b).
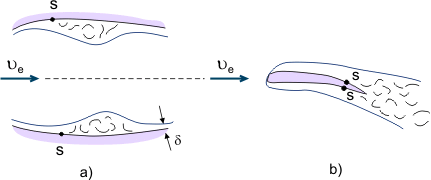
Figura 4. Fenomene de separare a straturilor-limită.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. și Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.
.