Sun, 18 Jun 2006
1+1=2
Principia Mathematica a lui Whitehead și Russell este faimoasă pentru că a avut nevoie de o mie de pagini pentru a demonstra că 1+1=2. Bineînțeles, demonstrează și multe alte lucruri. Dacă ar fi vrut să demonstreze doar că 1+1=2, probabil că ar fi ocupat doar jumătate din spațiu.
Principia Mathematica este o carte ciudată, care merită analizată atât din punct de vedere istoric, cât și matematic. Ea a fost scrisă în jurul anului 1910, iar logica matematică era pe atunci încă în fază incipientă, abia ieșită din transformarea la care au lucrat asupra eiPeano și Frege. Notația este oarecum obscură, deoarece notația matematică a evoluat substanțial de atunci. Și multe dintre tehnicile simple pe care acum le considerăm de la sine înțelese sunt absente.La fel ca un program de calculator prost scris, o mare parte din volumul Principia Mathematica este reprezentată de coduri repetate, secțiuni separate care spun în esență aceleași lucruri, deoarece autorii nu au învățat încă tehnicile care ar permite ca aceste secțiuni să fie combinate într-una singură.
De exemplu, secțiunea ∗22, „Calculul claselor”, începe prin a definirelația de subansamblu (∗22.01) și operațiile de uniune și intersecție a seturilor (∗22.02 și .03), complementul unui set (∗22.04) și diferența a două seturi (∗22.05). Se demonstrează apoi comutativitatea și asociativitatea uniunii și intersecției de seturi (∗22.51, .52, .57 și .7), diverse proprietăți precum !!\alpha\cap\alpha = \alpha!!! (∗22.5) și altele asemenea, ajungând la teoreme precum ∗22.92: !!\alpha\subansamblu\beta \frecvență dreaptă \alpha\cup(\beta -\alpha)!!!.
Secțiunea ∗23 este „Calculul relațiilor” și începe aproape exact în același mod, definind relația de subrelație (∗23.01), precum și operațiile de uniune și intersecție relațională (∗23.02 și .03), complementul unei relații (∗23.04) și diferența a două relații (∗23.05). Ulterior demonstrează comutativitatea și asociativitatea uniunii și intersecției relaționale (∗23.51, .52, .57 și .7), diverse proprietăți precum !!\alpha\dot\cap\alpha = \alpha!!! (∗22.5) și altele asemănătoare, ajungând la teoreme precum ∗23.92: !!\alpha\dot\subansamblu \beta \frecvență dreaptă \alpha\dot\cup(\beta \dot-\alpha)!!!.
Secțiunea ∗24 se referă la existența unor ansambluri, ansamblul nul !!\Lambda!!!, ansamblul universal !!{\rm V}!!, proprietățile lor și așa mai departe, iar apoi secțiunea ∗24 este dublată în ∗25 într-o serie de teoreme despreexistența relațiilor, relația nulă !!\dot\Lambda!!!, relația universală !!\dot {\rm V}!!!, proprietățile lor și așa mai departe.
Așa au procedat Whitehead și Russell în 1910. Cum am face-o noi astăzi? O relație între S și T este definită ca un subansamblu al luiS × T și, prin urmare, este un ansamblu. Uniunea, intersecția, diferența și celelalte operații sunt exact aceleași pentru relații ca și pentru seturi, deoarece relațiile sunt seturi. Toate teoremele despre uniunile și intersecțiile dintre relații, cum ar fi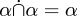 
, dispar pur și simplu, deoarece le-am demonstrat deja pentru seturi, iar relațiile sunt seturi. Relația nulă este setul nul. Relația universală este setul universal.
O mulțime de alte mecanisme dispar în 2006, din cauza unificării relațiilor și seturilor. Principia Mathematica are nevoie de o notație specială și de o definiție specială pentru rezultatul restrângerii unei relații la acele perechi al căror prim element este un membru al unui anumit set S, sau al cărui al doilea element este un membru al lui S, sau ale căror două elemente sunt membre ale lui S; în 2006 am folosi doar operația obișnuită de intersecție a seturilor și am vorbi despre R ∩(S×B) sau orice altceva.
Whitehead și Russell nu au putut face acest lucru în 1910 pentru că lipsea o piesă crucială a mașinăriei: perechea ordonată. În 1910 nimeni nu știa cum să construiască o pereche ordonată doar din logică și seturi. În 2006 (sau chiar în 1956), am defini perechea ordonată <a, b> ca fiind ansamblul {{a}, {a, b}}. Apoi am demonstra ca teoremă că <a, b> = <c, d> dacă și numai dacă a=c și b=d, folosind proprietățile seturilor. Apoi vom defini A×B ca fiind ansamblul tuturor p astfel încât p = <a,b> ∧ a ∈ A ∧ b∈ B. Apoi vom defini o relație între ansamblurile A și B ca fiind un subset al lui A×B. Atunci am obține toate ∗23 și ∗25 și o mare parte din ∗33 și ∗35 și ∗36 gratuit, și probabil și o mulțime de alte lucruri.
(Apropo, chestia {{a}, {a, b}} a fost inventată de Kuratowski. De obicei este atribuită lui Norbert Wiener, dar ideea luiWiener, deși similară, era de fapt mai complicată.)
Nu există perechi ordonate în Principia Mathematica,decât implicit. Abia dacă există chiar și seturi. Whitehead șiRussell vor să bazeze totul pe logică. Pentru Whitehead și Russell,noțiunea fundamentală este „funcția propozițională”, care este o funcție φ a cărei ieșire este o valoare de adevăr. Pentru fiecare astfel de funcție,există un set corespunzător, pe care ei îl denumesc prin !!\hat x\phi(x)!!!, setul tuturor x-urilor astfel încât φ(x) este adevărată. Pentru Whitehead și Russell, o relație este implicată de o funcție propozițională de două variabile, în mod analog cu modul în care un set este implicat de o funcție propozițională de o variabilă. În 2006, renunțăm la „funcții de două variabile” și vorbim doar despre funcții al căror (unic) argument este o pereche ordonată; o relație devine atunci ansamblul tuturor perechilor ordonate pentru care o funcție este adevărată.
Se presupune că Russell ar fi spus că descoperirea loviturii Sheffer (un singur operator logic din care pot fi construiți toți ceilalți operatori logici) a fost un progres extraordinar și că va schimba totul. Acest lucru ni se pare ciudat acum, deoarece descoperirea cursei Sheffer pare atât de simplă și nu schimbă cu adevărat nimic important. Trebuie doar să adăugați o notă la începutul capitolului 1 care să spună că ∼p și p∨q suntabrevieri pentru p|p și, respectiv, p|p.|.q|q, să demonstrați cele cinci axiome fundamentale și să lăsați restul la fel. Dar Russell ar fi putut, cu oarecare dreptate, să spună același lucru despre descoperirea că perechile ordonate pot fi interpretate ca seturi, o descoperire simplă care ar fi transformat cu adevărat Principia Mathematica într-o lucrare cu totul diferită.
În orice caz, având acest context, putem discuta despre demonstrația din Principia Mathematica a lui 1+1=2. Aceasta apare destul de târziu în Principia Mathematica, în secțiunea ∗102. Versiunea mea integrală merge doar până la ∗56, dar este suficient de departe pentru a ajunge la importantă teoremă precursoare, ∗54.43, scanată mai jos:
Notația poate fi copleșitoare, așa că haideți să ne concentrăm doar pe enunțarea teoremei, să ignorăm tot restul, chiar și observația utilă din partea de jos:
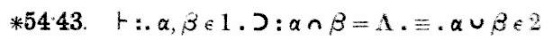
Aceasta este teorema care este demonstrată; ceea ce urmează este demonstrația.
Acum ar trebui să explic notarea, care s-a schimbat oarecum din 1910. În primul rând, Principia Mathematica folosește notația „puncte” a lui Peano pentru a dezambiguiza precedența, unde acum folosim în schimb paranteze. Este nevoie de o oarecare obișnuință cu notația cu puncte, dar are câteva avantaje distincte față de paranteze. Ideea este aceea că se indică gruparea prin introducerea punctelor, astfel încât (1+2)×(3+4)&înmulțit cu(5+6) se scrie ca1+2.×.3+4.×.5+6. Subformula din mijloc se află între o pereche de puncte. Subformula (1+2) este, de asemenea, între o pereche de puncte, dar punctul de la capătul din stânga este superfluu și îl omitem; în mod similar, subformula (5+6) este delimitată de un punct în stânga și de sfârșitul formulei în dreapta.
Ce se întâmplă dacă trebuie să aninați paranteze? Atunci se folosesc mai multe puncte. Un punct dublu (:) este ca un singur punct, dar mai puternic. De exemplu, scriem ((1+2)×3)+4 ca 1+2 . × 3 : + 4, iar punctul dublu izolează întregul 1+2 . × 3 într-o singură subformulă la care se aplică +4.
Câteodată aveți nevoie de mai multe niveluri de precedență, și atunci folosiți puncte triple (.: și :.) și cvadruple (::). Această formulă, după cum vedeți, arepuncte duble și triple. Transpunând punctele în notația standard de paranteză, avem $$\ast54.43. \vdash ((\alpha, \beta \în 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \în 2)))$$$. Aceasta are un aspect ceva mai dezordonat decât versiunea cu puncte, iar în cazul formulelor incomplicate puteți avea probleme în a vă da seama ce paranteze se potrivesc cu care. Cu punctele, este întotdeauna ușor. Așadar, cred că este un pic nefericit că această convenție a ieșit din uz.
Simbolul !!\vdash!! nu s-a schimbat; înseamnă că formula la care se aplică se afirmă că este adevărată. !!\supset!! este implicație logică, iar !!\equiv!! este echivalență logică. Λ este setul gol, pe care în prezent îl scriem ∅. ∩ ∪ și ∈ au semnificațiile lor moderne: ∩ și ∪ sunt operatorii de intersecție și de uniune a ansamblurilor, iar x∈y înseamnă că x este un element al ansamblului y.
Celelalte puncte sunt semantice. α și β sunt ansambluri. 1înseamnă ansamblul tuturor seturilor care au exact un element. Adică, este ansamblul { c : există a astfel încât c = {a } }. Teoremele despre 1 includ, de exemplu:
- că Λ∉1 (∗52.21),
- că dacă α∈1 atunci există un anumit x astfel încât α ={x} (∗52.1), și
- că {x}∈1 (∗52.22).
2 este, în mod similar, ansamblul tuturor ansamblurilor care au exact două elemente. O teoremă importantă despre 2 este ∗54.3, care spune că $$\ast54.3. \vdash 2 = \hat\alpha\{ (\există x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\în 1 \}.$$În notația din Principia Mathematica, {x}, ansamblul care îl conține pe x și nimic altceva, se scrie ι’x, astfel încât teorema spune că 2 este identic cu ansamblul tuturor elementelor α astfel încâtα are un anumit element x , care, atunci când este eliminat din α,lasă un ansamblu cu 1 element.
Iată deci din nou teorema ∗54.43:
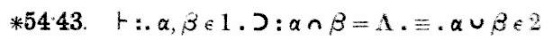
Afirmă că dacă seturile α și β au fiecare exact un element, atunci ele sunt disjuncte (adică nu au elemente în comun) dacă și numai dacă uniunea lor are exact două elemente.
Demonstrația, care apare în scanarea de mai sus după cuvântul „Dem.” (prescurtare de la „demonstrație”) sună astfel:
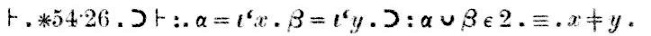
„Teorema ∗54.26implică că dacă α = {x} și β = {y}, atunciα∪β are 2 elemente dacă și numai dacă x estediferit de y.”
„Prin teorema ∗51.231, acest ultim aspect (x este diferit dey) este adevărat dacă și numai dacă {x} și {y} sunt disjuncte.”
„Prin ∗13.12, acest ultim bit ({x} și {y} sunt disjuncte) este adevărat dacă și numai dacă α și β sunt ele însele disjuncte.” Concluzia parțială în acest punct,care este etichetată (1), este că dacă α = {x} și β ={y}, atunci α∪β ∈ 2 dacă și numai dacăα∩β = Λ.
Demonstrația continuă: „Concluzia (1), cu teoremele ∗11.11 și ∗11.35,implică faptul că dacă există x și y astfel încât α este{x} și β este {y}, atunci α∪β ∈ 2 dacă și numai dacă α și β sunt disjuncte.” Această concluzie este etichetată (2).
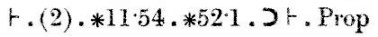
În cele din urmă, concluzia (2), împreună cu teoremele ∗11.54 și ∗52.1,implică teorema pe care am încercat să o demonstrăm.
Poate că ceea ce trebuie observat aici este cât de mici sunt pașii.∗54.26, de care depinde foarte mult această teoremă, este aproape la fel; ea afirmă că {x}∪{y} ∈ 2 dacă și numai dacă x≠y. ∗54.26, la rândul său, depinde de ∗54.101, care spune că α are 2 elemente dacă și numai dacă există x șiy, care nu sunt identice, astfel încât α = {x} ∪{y}. ∗54.101 este doar un pic diferit de definiția lui 2. Teorema ∗51.231 spune că {x} și {y} sunt disjuncte dacă și numai dacă x și y sunt diferite.∗52.1 este o proprietate de bază a lui 1; am văzut-o înainte.
Celelalte teoreme citate în demonstrație sunt chestiuni tehnice foarte mici. ∗11.54 spune că puteți lua o afirmație că două lucruri există și o puteți separa în două afirmații, fiecare dintre ele afirmând că unul dintre lucruri există. ∗11.11 este și mai subțire: spune că, dacă φ(x, y) este întotdeauna adevărată, atunci se poate atașa un cuantificator universal și se poate afirma că φ(x, y) este adevărată pentru toate x și y. ∗13.12 se referă la înlocuirea egalului cu egalul: dacă x și y sunt identice, atunci x posedă o proprietate ψ dacă și numai dacă și y o posedă și el.
Nu am văzut ultimele părți din Principia Mathematica, pentru că exemplarul meu se oprește după secțiunea ∗56, iar chestiunile de aritmetică sunt mult mai târziu. Dar această teoremă are în mod clar sensul de 1+1=2 în ea, iar teorema ulterioară (∗110.643)care afirmă de fapt 1+1=2 depinde puternic de aceasta.
Chiar dacă nu sunt complet sigur de ceea ce se va întâmpla mai târziu(am pierdut deja mult prea mult timp cu asta ca să mai pierd timp pentru a obține versiunea completă din bibliotecă), pot face o presupunere. Principia Mathematica va defini numărul 17 ca fiind setul tuturor seturilor cu 17 elemente, și în mod similar pentru orice alt număr; utilizarea simbolului 2 pentru a reprezenta setul tuturor seturilor cu 2 elemente prefigurează acest lucru. Ansamblurile tuturor seturilor de o anumită mărime vor fi apoi identificate ca „numere cardinale”.
Principiul Matematicii va defini suma numerelor cardinale p și qîn felul următor: se ia un ansamblu reprezentativ a din p;a are p elemente. Se ia un ansamblu reprezentativ b din q; b are q elemente. Fie c =a∪b. Dacă c este un membru al unui număr cardinal r și dacă a și b sunt disjuncte, atunci suma lui p și q este r.
Cu această definiție, puteți demonstra proprietățile obișnuite dezirabile ale adunării, cum ar fi x + 0 = x, x + y = y + x și 1 + 1 = 2.
În special, 1+1=2 rezultă direct din teorema ∗54.43; este exact ceea ce ne dorim, deoarece pentru a calcula 1+1, trebuie să găsim doi reprezentanți disjunși ai lui 1 și să luăm uniunea lor; ∗54.43 afirmă că uniunea trebuie să fie un element al lui 2, indiferent de reprezentanții pe care îi alegem, astfel încât 1+1=2.
Post scriptum: Peter Norvig spune că circumflexul din notația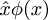 
dinPrincipia Mathematica este sursa ultimă a folosirii cuvântuluilambda pentru a desemna o funcție anonimă în limbajele de programare Lisp și Pythonprogramare. Sunt sigur că știți că aceste limbaje obțin „lambda” de la utilizarea literei grecești λ de către Alonzo Church pentru a reprezenta abstractizarea funcțiilor în „λ-calculul” său: În Lisp,(lambda (u) B) este o funcție care ia un argumentu și returnează valoarea lui B; în λ-calculus,λu.B este o funcție care ia un argumentu și returnează valoarea lui B. Norvig spune că Church plănuia inițial să scrie funcțiaλu.B ca û.B, dar imprimanta sa nu putea face accente circumflexe. Așa că s-a gândit să mutecircumflexul la stânga și să folosească în schimb un lambda cu majusculă:Λu.B. Majuscula Λ semăna prea mult cu literele Λ și ∧, ceea ce era derutant, așa că a folosit în schimb lambdaλ cu minusculă.
Post post scriptum: Toată lumea spune întotdeauna „Russell și Whitehead”.Rezultatele Google pentru „Russell și Whitehead” le depășesc pe cele pentru „Whitehead și Russell” cu doi la unu, de exemplu. De ce? Pe copertăși pe pagina de titlu scrie „Alfred North Whitehead și Bertrand Russell,F.R.S.”. Cum și când a pierdut Whitehead din prima poziție?
link permanent
.