- Text
- Problem
- Måluppfyllelse
- Fyll i blanketterna
- Flera val
- Förteckning
Den teoretiskt sett bästa metoden för att redovisa avskrivningar är effektivräntemetoden. Räntekostnaden är en konstant procentandel av obligationens bokförda värde, snarare än ett lika stort belopp i dollar varje år. Den teoretiska förtjänsten vilar på det faktum att ränteberäkningen överensstämmer med den grund på vilken obligationen prissattes.
Räntekostnaden beräknas som den effektiva räntesatsen gånger obligationens bokförda värde för varje period. Amorteringsbeloppet är skillnaden mellan den kontant betalda räntan och det beräknade beloppet för räntekostnaden för obligationen.
Premieexempel
Håll dig till minnet att när Schultz emitterade sina obligationer för att ge 6 % avkastning fick företaget 108 530 dollar. Den effektiva räntan för de första sex månaderna är således 108 530 dollar X 6 % X 6/12 = 3 255,90 dollar. Av detta belopp betalas 4 000 dollar kontant och 744,10 dollar (4 000 dollar – 3 255,90 dollar) är premieavskrivning. Amorteringen av premien minskar skuldens bokförda nettovärde till 107 785,90 dollar (108 530 dollar – 744,10 dollar). Detta nya saldo skulle sedan användas för att beräkna den effektiva räntan för nästa period. Denna process skulle upprepas varje period, enligt följande tabell:
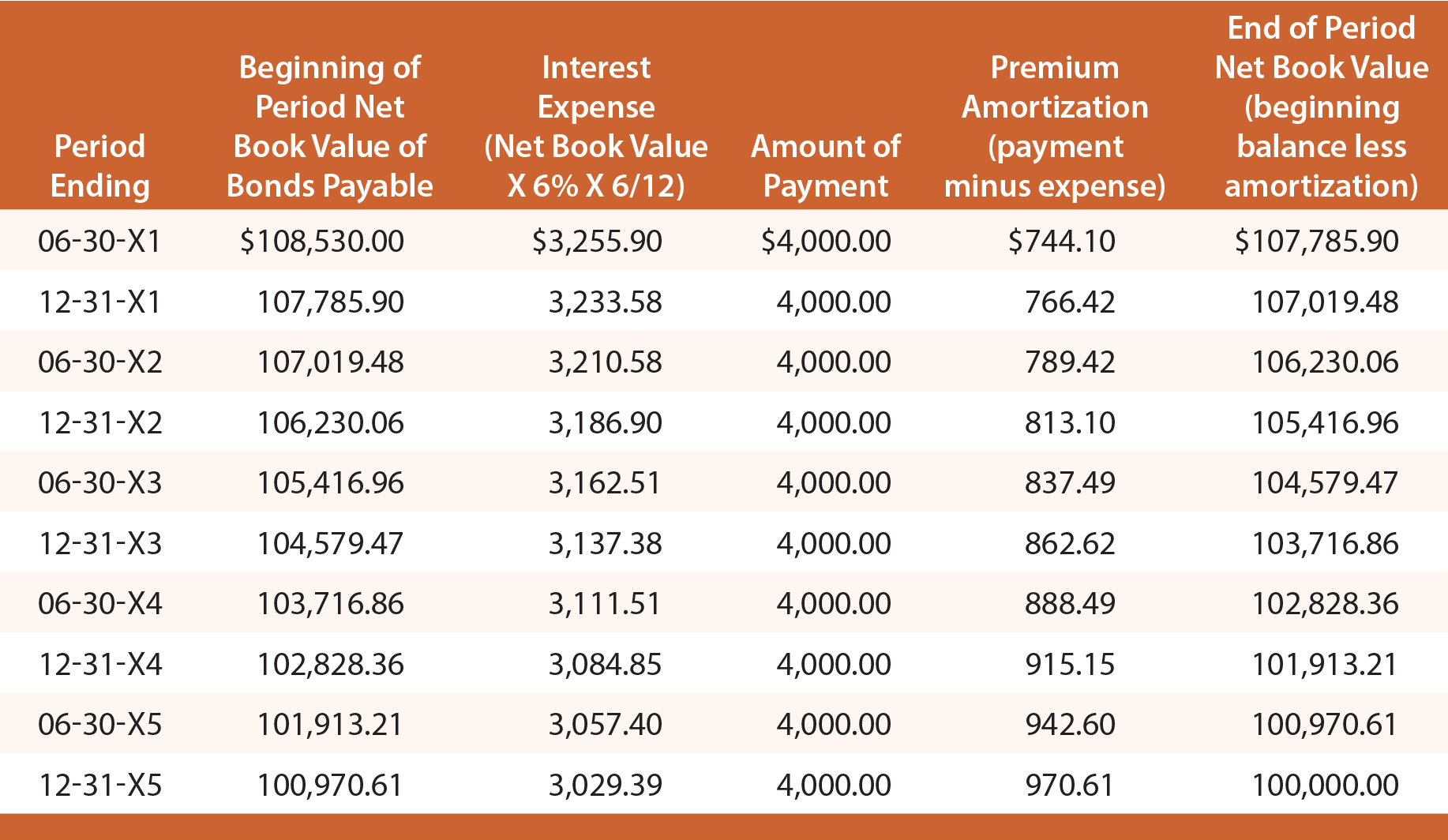
Den första journalanteckningen för att registrera emissionen av obligationerna och den slutliga journalanteckningen för att registrera återbetalningen på förfallodagen skulle vara identiska med dem som demonstreras för den linjära metoden. Däremot skulle varje journalpost för att registrera den periodiska redovisningen av räntekostnader variera och kan bestämmas genom hänvisning till föregående amorteringstabell.
Följande post skulle bokföra ränta den 30 juni 20X3:

Följande balansräkning skulle vara lämplig den 30 juni 20X3:

Redovisningsexempel
Håll dig till minnet att när Schultz emitterade sina obligationer för att ge 10 % avkastning, erhöll företaget endast 92 278 dollar. Den effektiva räntan för de första sex månaderna är således 92 278 dollar X 10 % X 6/12 = 4 613,90 dollar. Av detta belopp betalas 4 000 dollar kontant och 613,90 dollar är diskonteringsavskrivning. Diskonteringsavskrivningen ökar skuldens bokförda nettovärde till 92 891,90 dollar (92 278,00 dollar + 613,90 dollar). Detta nya saldo skulle sedan användas för att beräkna den effektiva räntan för nästa period. Denna process skulle upprepas varje period enligt följande:
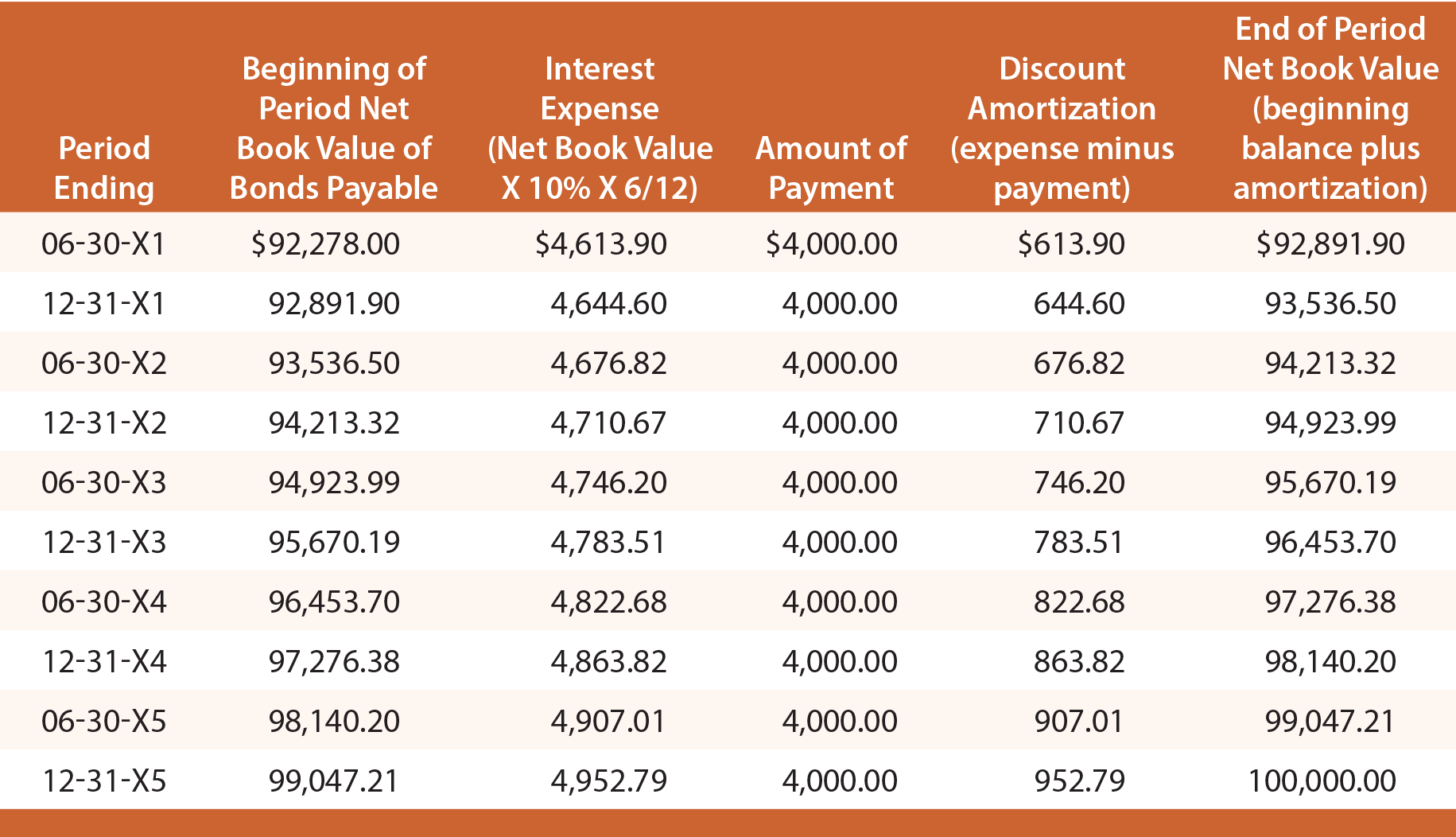
Varje journalpost för att registrera den periodiska redovisningen av räntekostnader skulle variera och kan bestämmas genom hänvisning till föregående amorteringstabell. Exempelvis skulle följande bokföring bokföra ränta den 30 juni 20X3 och resultera i nedanstående balansräkning: