Ett gränsskikt är ett tunt skikt av viskös vätska nära den fasta ytan på en vägg i kontakt med en rörlig ström där (inom dess tjocklek δ) flödeshastigheten varierar från noll vid väggen (där flödet ”klibbar” fast vid väggen på grund av sin viskositet) upp till Ue vid gränsen, vilket ungefär (med ett fel på 1 %) motsvarar hastigheten i den fria strömmen (se figur 1). Strängt taget är δ ett godtyckligt värde eftersom friktionskraften, som beror på den molekylära interaktionen mellan vätskan och den fasta kroppen, minskar med avståndet från väggen och blir lika med noll vid oändligheten.
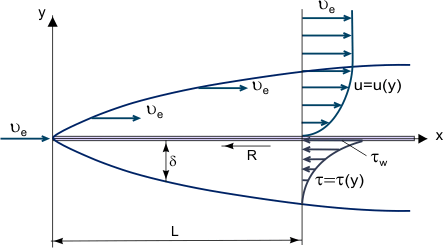
Figur 1. Tillväxt av ett gränsskikt på en platt platta.
Det grundläggande begreppet gränsskikt föreslogs av L. Prandtl (1904), det definierar gränsskiktet som ett lager av vätska som utvecklas i flöden med mycket höga Reynoldstal Re, det vill säga med relativt låg viskositet jämfört med tröghetskrafterna. Detta observeras när kroppar utsätts för luftströmmar med hög hastighet eller när kroppar är mycket stora och luftströmmarnas hastighet är måttlig. I detta fall, i ett relativt tunt gränsskikt, kan friktionens skjuvspänning (viskös skjuvkraft): τ = η (där η är den dynamiska viskositeten; u = u(y) – ”profilen” för gränsskiktets longitudinella hastighetskomponent, se figur 1) vara mycket stor; särskilt vid väggen där u = 0 och τw = ηw även om viskositeten i sig kan vara ganska liten.
Det är möjligt att bortse från friktionskrafter utanför gränsskiktet (jämfört med tröghetskrafter) och på grundval av Prandtls koncept betrakta två flödesregioner: gränsskiktet där friktionseffekterna är stora och den nästan inviscida flödeskärnan. Om man utgår från att gränsskiktet är ett mycket tunt skikt (δ << L, där L är den karakteristiska linjära dimensionen hos den kropp över vilken flödet sker eller hos den kanal som innehåller flödet, och där tjockleken minskar med ökningen av Re, figur 1), kan man uppskatta storleksordningen på gränsskiktets tjocklek med hjälp av följande relation:
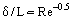
Till exempel, när ett flygplan flyger med Ue = 400 km/tim, är gränsskikttjockleken vid vingens bakkant med 1 meters chord (profillängd)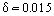 
m. Som experimentellt fastställts utvecklas ett laminärt gränsskikt vid kroppens inloppsdel. Under påverkan av vissa destabiliserande faktorer blir gränsskiktet gradvis instabilt och övergången till turbulenta flöden äger rum. Särskilda experimentella undersökningar har visat att det finns en övergångsregion mellan turbulenta och laminära områden. I vissa fall (t.ex. vid hög turbulensnivå i det externa flödet) blir gränsskiktet turbulent omedelbart nedströms från stagnationspunkten i flödet. Under vissa förhållanden, t.ex. vid ett kraftigt tryckfall, sker ett omvänt fenomen i accelererande turbulenta flöden, nämligen flödesrelaminarisering.
Trots sin relativa tunnhet är gränsskiktet mycket viktigt för att initiera processer av dynamisk interaktion mellan flödet och kroppen. Gränsskiktet bestämmer det aerodynamiska motståndet och lyftet hos det flygande fordonet, eller energiförlusten för vätskeflöde i kanaler (i det här fallet ett hydrodynamiskt gränsskikt eftersom det också finns ett termiskt gränsskikt som bestämmer den termodynamiska interaktionen vid värmeöverföring).
Beräkningen av gränsskiktsparametrarna bygger på lösningen av ekvationer som erhålls från Navier-Stokes ekvationer för viskös vätskerörelse, som först förenklas avsevärt med hänsyn till gränsskiktets tunnhet.
Lösningen som föreslogs av L. Prandtl är i huvudsak den första termen i en potensserieexpansion av Navier-Stokes ekvation, där serieexpansionen utförs för potenser av den dimensionslösa parametern (δ/L). Den mindre parametern i denna term är i nollpotens så att gränsskiktsekvationen är nollnärmningen i en asymptotisk expansion (vid stort Re) av gränsskiktsekvationen (asymptotisk lösning).
En omvandling av Navier-Stokes-ekvationen till gränsskiktsekvationer kan demonstreras genom att härleda Prandtl-ekvationen för laminärt gränsskikt i ett tvådimensionellt inkompressibelt flöde utan kroppskrafter.
I det här fallet blir systemet av Navier-Stokes-ekvationer:
Efter att ha utvärderat storleksordningen för vissa termer i ekv. (2) och genom att bortse från små termer blir systemet av Prandtl-ekvationer för laminärt gränsskikt:
där x, y är longitudinella och laterala koordinater (figur 1), v är hastighetskomponenten längs ”y”-axeln, p, tryck, t, tid och n, kinematisk viskositet.
Gränsskiktet är tunt och hastigheten vid dess yttre kant Ue kan bestämmas tillräckligt och noggrant som hastigheten för ett idealt (inviscid) vätskeflöde längs väggen beräknat upp till den första approximationen, utan att ta hänsyn till gränsskiktets omvända verkan på det yttre flödet. Den longitudinella tryckgradienten = (vid p(y) = const) i ekv. (3) kan beskrivas med hjälp av Eulers rörelseekvation för en ideal vätska. Utifrån ovanstående kan Prandtl-ekvationer i sin finita form skrivas som:
Detta är ett system av paraboliska, icke-linjära partiella differentialekvationer av andra ordningen som löses med initial- och randvillkor
Systemet av ekvationer (4) skrivs för faktiska värden på hastighetskomponenterna u och v. För att generalisera de ekvationer som erhållits för turbulenta flöden bör det välkända förhållandet mellan faktiska, medelvärdesberäknade och pulserande komponenter av parametrar för turbulenta flöden användas. För hastighetskomponenterna finns det till exempel relationer som förbinder de faktiska u- och v-komponenterna, de genomsnittliga ū- och 
och de pulserande u’- och v’-komponenterna:
Efter några omarrangemang är det möjligt att få fram ett annat ekvationssystem från system (3), särskilt för stationärt flöde:
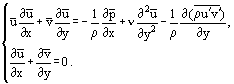
Med hjälp av följande relation för friktionsskavspänning i gränsskiktet:
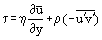
och med hänsyn till att i det laminära gränsskiktet är u = u’ och
det är möjligt att skriva om Prandtl-ekvationerna i en form som är giltig för både laminära och turbulenta flöden:
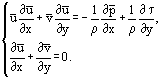
De enklaste lösningarna har erhållits för ett laminärt gränsskikt på en tunn platt platta i ett tvådimensionellt, parallellt flöde av inkompressibel vätska (figur 1). I detta fall gör uppskattningen av storleksordningen för ekvationstermerna: x ~ L, y ~ δ, δ ~
det möjligt att kombinera variablerna x och y i en relation
och att reducera lösningen av ekvation (8) (vid dp/dx = 0) till att bestämma beroendet av u och v på den nya parametern ξ. Med hjälp av välkända relationer mellan hastighetskomponenterna u, v och strömningsfunktionen ψ
är det å andra sidan möjligt att få fram en vanlig icke-linjär differentialekvation av tredje ordningen, i stället för systemet av partiella differentialekvationer (8)
Här är f(ξ) den okända funktionen av variabeln ξ: f = ƒ =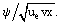
Den första numeriska lösningen av Eq. (10) erhölls av Blasius (1908) under randvillkor som motsvarar de fysiska villkoren för gränsskiktet vid y = 0: u = 0, v = 0; vid y → ∞; u → Ue (Blasius gränsskikt).
I figur 2 jämförs resultaten av Blasius lösning (heldragen linje) med experimentella data. Med hjälp av dessa data är det möjligt att utvärdera det viskösa gränsskiktets tjocklek. Vid ξ 
2,5, (u/Ue 0,99) (figur 2); följaktligen får vi från Eq. (9) följande: 
Figur 2.
Från Blasius numeriska beräkningar av värdet av den andra derivatan av funktionen f(ξ) vid skjuvspänningen för väggfriktion är förhållandet i detta fall:
Friktionskraften R, som verkar på båda sidorna av plåten med en längd på L (figur 1), bestäms också från Eq. (11):
som i friktionskoefficienten för platta plattor:
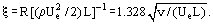
Trots att Prandtl-ekvationerna är mycket enklare än Navier-Stokes-ekvationerna erhölls deras lösningar för ett begränsat antal problem. För många praktiska problem är det inte nödvändigt att bestämma hastighetsprofiler i gränsskiktet, utan endast tjocklek och skjuvspänning. Denna typ av information kan erhållas genom att lösa den integrerade impulsekvationen
Den integrerade relationen (12) är giltig både för det laminära och turbulenta gränsskiktet.
Funktioner som inte var kända på förhand men som karaktäriserar fördelningen av vätskeparametrar över skikttjockleken δ ligger under integralen i ekv. (12). Och felet vid beräkning av integralen är mindre än felet i den ungefärligt antagna integrandfunktionen ρu = ρu(y). Detta skapar förutsättningar för att utveckla approximativa metoder för beräkning av gränsskiktsparametrar som är mindre tidskrävande än de exakta metoderna för integrering av Prandtl-ekvationer. Det grundläggande konceptet föreslogs först av T. von Karman, som införde en sådan godtycklig skikttjocklek δ*
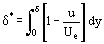
och impulsförskjutningstjocklek δ**
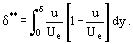
därmed kan vi omvandla Eq. (12) för ett tvådimensionellt gränsskikt av inkompressibel vätska till:
Det finns tre okända funktioner i ekv. (15), nämligen δ* = δ*(x), δ** = δ**(x) och τw = τw(x) .
Lösningen av en ordinär differentialekvation som ekv. (15) kräver vanligtvis antagande (eller representation) av hastighetsfördelningen (hastighetsprofilen) över gränsskiktets tjocklek som en funktion av vissa karakteristiska parametrar (formparametrar), och det kräver också användning av empiriska data om förhållandet mellan friktionskoefficienten Cf = 2τw/(ρU2e) och gränsskiktets godtyckliga tjocklek (friktionslagen).
Några bestämda fysikaliska förklaringar kan ges vad gäller värdena för δ* och δ**. Integrandfunktionen i ekv. (13) innehåller efter omarrangemang en term (Ue – u) som karakteriserar hastighetsminskningen. Integralen i ekv. (14) kan således betraktas som ett mått på minskningen av flödeshastigheten genom gränsskiktet jämfört med det perfekta vätskeflödet vid hastigheten Ue. Å andra sidan kan värdet δ* betraktas som ett mått på avvikelsen längs en normal till väggen (längs y-axeln) av den yttre strömningslinjen under påverkan av friktionskrafter. Utifrån denna betraktelse av den integrala strukturen i ekv. (14) är det möjligt att dra slutsatsen att δ** karakteriserar momentminskningen i gränsskiktet under påverkan av friktion.
Följande relationer är giltiga:
där H är en formparameter för hastighets-profilen i gränsskiktet. Till exempel, för linjär fördelning u = ky,
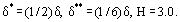
För närvarande används så kallade semi-empiriska teorier i stor utsträckning för att förutsäga turbulenta gränsskiktsparametrar. I detta fall antas att den totala friktionsspänningen τ i ett turbulent gränsskikt är en summa
Här är τT ytterligare (turbulent eller Reynolds) friktionsspänning, i synnerhet i ett inkompressibelt flöde
se Eq. (7).
Denna representation är direkt kopplad till systemet av rörelseekvationer i gränsskiktet (6). I det kompressibla gränsskiktet kan densitetspulserna anses vara resultatet av temperaturpulser
där β = (1/T) är den volymetriska expansionskoefficienten.
Tillkommande halvempiriska hypoteser om turbulensens momentumöverföring används för att bestämma τT. Till exempel
där ηT är den dynamiska koefficienten för turbulent viskositet som introducerades av J. Boussinesq 1877.
Med utgångspunkt i begreppet likhet mellan molekylärt och turbulent utbyte (likhetsteorin) introducerade Prandtl hypotesen om blandningslängd (die Mischungsweg). Blandningslängden 1 är den väg som en ändlig vätskevolym (”mol”) passerar från ett lager med genomsnittlig rörelse till ett annat utan att ändra sitt momentum. I enlighet med detta villkor härledde han en ekvation som visade sig vara grundläggande för gränsskiktsteorin:
För det turbulenta området i gränsskiktet nära väggen, L. Prandtl ansåg att längden 1 är proportionell mot y
där κ är en empirisk konstant.
Närmast väggen, där ηT << η, är den viskösa molekylära friktionen en avgörande faktor. Tjockleken på denna del av gränsskiktet δ1, som kallas laminärt eller visköst underlag, är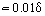
. Utanför underlagret ökar värdet på ηT och når flera storleksordningar större än η. På motsvarande sätt är τT > 0 = η i denna zon av gränsskiktet som kallas den turbulenta kärnan τT > 0 = η. Ibland delas den turbulenta kärnan upp i buffertzonen, där den laminära och turbulenta friktionen har ett jämförbart värde, och den utvecklade zonen, där τT >> τ0. För denna region kan man efter integrering av ekv. (18) och med hänsyn till ekv. (19) härleda ett uttryck för den logaritmiska hastighetsprofilen:
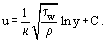
Om dimensionslösa (eller universella) koordinater används:
där
är den s.k. dynamiska hastigheten (eller friktionshastigheten), ekv. (20) kan skrivas om i följande form:
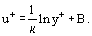
Hastighetsfördelningsrepresentation i universalkoordinater och matematiska modeller för turbulenta viskositetskoefficienter behandlas mer detaljerat i avsnittet Turbulent strömning.
En av de aktuella versionerna av den semi-empiriska teorin för turbulenta gränsskikt som utvecklats av S. S. Kutateladze och A. I. Leontiev bygger på den så kallade asymptotiska teorin för turbulenta gränsskikt vid Re → ∞ där tjockleken på det laminära (viskösa) underlagret δ1 minskar med högre hastighet än δ, vilket resulterar i att (δ1/δ) → 0.
Under dessa förhållanden utvecklas ett turbulent gränsskikt med ”försvinnande viskositet”. I detta skikt är η → 0 men inte lika med noll och i detta avseende skiljer sig skiktet från det perfekta flödet. Begreppet relativ friktionslag, som introducerades av S. S. Kutateladze och A. I. Leontiev (1990), indikerar
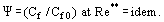
Lagen definieras som förhållandet mellan friktionskoefficienten Cf för det aktuella tillståndet och värdet av Cf0 för ”standard”-förhållanden på en plan, ogenomtränglig platta som flyter runt av ett inkompressibelt, isotermiskt flöde, där båda koefficienterna erhålls för Re** = Ueδ**/ν. Det visas att vid Re → ∞; η → 0; och Cf → 0 har den relativa variationen av friktionskoefficienten under påverkan av sådana störande faktorer som tryckgradient, kompressibilitet, icke isotermi, injektion (sugning) genom en porös vägg etc. ett ändligt värde.
De ekvationer som härletts för att beräkna värdet av Ψ har en viktig egenskap som gör Ψ oberoende av empiriska turbulenskonstanter. I enlighet med det grundläggande konceptet för det integrala ”tillvägagångssättet” omvandlas den integrala impulsekvationen till:
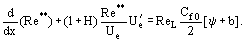
Här är 
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) permeabilitetsparametrarna för det fall att en gas med densiteten ρw sprutas in genom en genomsläpplig vägg med hastigheten vw. För att bestämma funktionen Re** = Re**
är det nödvändigt att beräkna fördelningen
För detta ändamål gäller principen om superposition av störande faktorer
I Eq. 24 representerar varje multiplikator den relativa friktionslagen med hänsyn till effekten av en av faktorerna, bland annat kompressibiliteten ΨM, temperatur- (eller entalpi-) huvudet ΨT, injektionen ΨB, tryckgradienten ΨP och andra.
De grundläggande begreppen för gränsskiktet skapar förutsättningar för att förklara sådana fenomen som flödesavskiljning från ytan under inflytande av flödeströgheten, fördröjning av det viskösa flödet genom väggen och negativ tryckgradient som verkar i uppströms riktning = 0 eller < 0.
Om tryckgradienten är ogynnsam på ytan mellan sektionerna ”1-4” (se figur 3) förändras hastighetsfördelningen u = u(x,y) i gränsskiktet gradvis; den blir ”mindre fyllig”, minskar lutningen i de vätskestrålar som befinner sig närmare väggen och som har mindre mängd kinetisk energi (se hastighetsprofilens former i figur 3) och som tränger långt nedströms in i området med ökat tryck. I vissa sektioner, till exempel sektion ”4”, bromsas de vätskepartiklar som befinner sig på strömningslinjen ”a-a” (streckad linje i figur 3) – efter att helt ha uttömt sin kinetiska energi – upp (ua = 0).
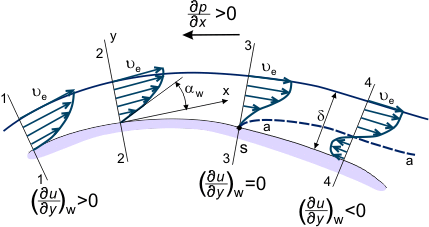
Figur 3. Gränsskikt i strömning över en täckt yta.
Det statiska trycket och värdet av tryckgradienten varierar inte över gränsskiktets tjocklek. Därför börjar vätskepartiklar som befinner sig närmare väggen än linjen ”a-a” och som har ännu mindre energi att röra sig i motsatt riktning under påverkan av tryckgradienten i sektion ”4-4” (se figur 3). På så sätt uppstår förhållandet:
På detta sätt förändras hastighetsprofilen på vissa ställen på ytan. Denna förändring kännetecknas av att tecknet på derivatan w ändras från positivt (avsnitt 2, figur 3) till negativt (avsnitt 4). Det är naturligtvis också möjligt att definiera det avsnitt där w = 0 (avsnitt 3, figur 3). Detta kallas gränsskiktssektionen (motsvarande punkt ”S” på ytan av denna sektion är separationspunkten). Det kännetecknas av att det utvecklas en zon med omvänt flöde – flödet runt kroppen är inte längre jämnt, gränsskiktet blir betydligt tjockare och de yttre flödesströmlinjerna avviker från ytan på den kropp som flygs runt. Nedströms separationspunkten är den statiska tryckfördelningen över skiktets tjocklek inte stadig och den statiska tryckfördelningen längs ytan motsvarar inte tryckfördelningen i det externa, inviscida flödet.
Separationen följs av utvecklingen av omvänd flödeszon och virvlar, där den kinetiska energi som tillförs från det externa flödet omvandlas till värme under inverkan av friktionskrafter. Flödesseparationen, som åtföljs av energidissipation i de omvända flödesvirvelzonerna, resulterar i sådana oönskade effekter som ökad dragkraft hos flygande fordon eller hydrauliska förluster i kanaler.
Å andra sidan används separerade flöden i olika anordningar för intensiv blandning av vätska (t.ex. för att förbättra blandningen av bränsle och luft i förbränningskamrar i motorer). När viskösa vätskor strömmar i kanaler med varierande tvärsnitt (växlande tryckgradient) kan separationszonen vara lokal om diffusorsektionen följs av konfusorsektionen, där det separerade flödet återigen kommer att fästa vid ytan (se figur 4a). När flödet separeras från kroppens bakkant (t.ex. från vingens bakkant) bildas det så kallade kölvattnet av ”sammanlänkande” gränsskikt (se figur 4b).
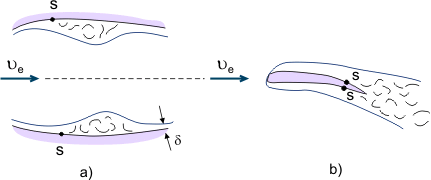
Figur 4. Gränsskiktsseparationsfenomen.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. and Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.