By Leave a Comment on Matematik för de fria konsterna

Nät

Ett sista sätt att representera ett fast ämne är att använda ett nät. Om du klipper ut ett nät kan du vika det till en modell av en figur. Nät kan också användas för att analysera ett enskilt fast ämne. Här är ett exempel på ett nät för en kub.

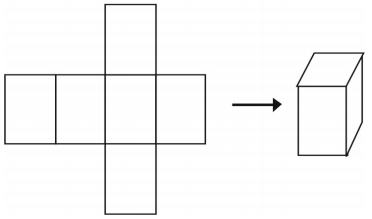
Det finns mer än ett sätt att göra ett nät för en enskild figur.

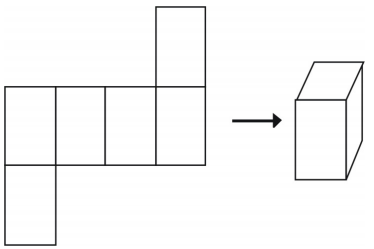
Det är dock inte alla arrangemang som skapar en kub.

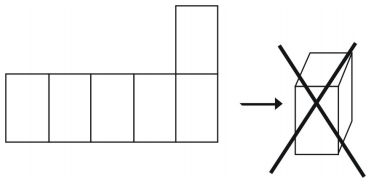
Exempel 1

Vad för slags figur skapar nätet? Rita figuren.

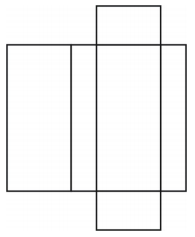
Nätet skapar ett lådformat rektangulärt prisma som visas nedan.

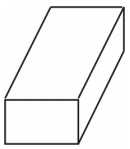
Exempel 2

Vilken typ av nät kan du rita för att representera den visade figuren? Rita nätet.

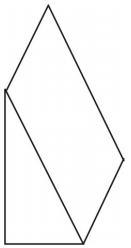
Ett nät för prismat visas. Andra nät är möjliga.

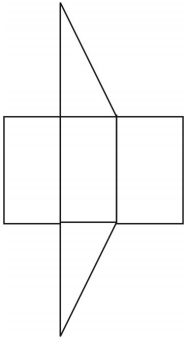
Revisionsövningar

Rita ett nät för var och en av följande:

Svar

Prisma

Ett prisma är en tredimensionell figur med ett par parallella och kongruenta ändar, eller baser. Sidorna i ett prisma är parallellogram. Prismor identifieras genom sina baser.

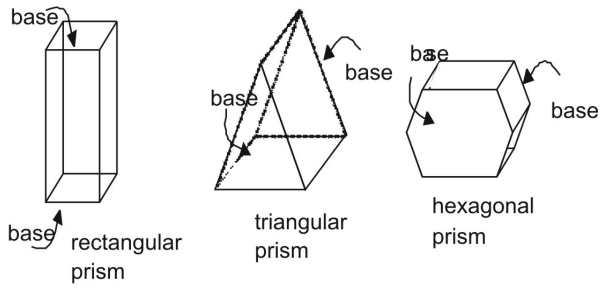
Områdesarea av ett prisma med hjälp av nät

Prismerna ovan är rätvinkliga prismor. I ett rätvinkligt prisma är sidosidorna vinkelräta mot baserna i prismat. Jämför ett rätvinkligt prisma med ett snett prisma, där sidorna och baserna inte är vinkelräta.

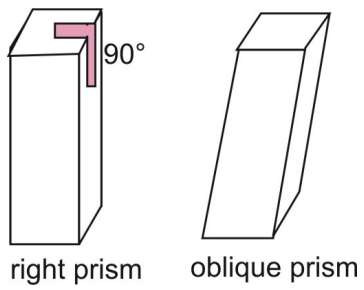
Två postulat som gäller för area är areakongruenspostulatet och areaadditionspostulatet.

Areakongruenspostulatet: Om två polygoner (eller plana figurer) är kongruenta är deras areor kongruenta.
Area Addition Postulat: Om två polygoner (eller plana figurer) är kongruenta är deras areor kongruenta:

Du kan använda ett nät och postulatet om areauppräkning för att hitta ytan på ett rätvinkligt prisma med hjälp av ett nät och postulatet om areauppräkning.

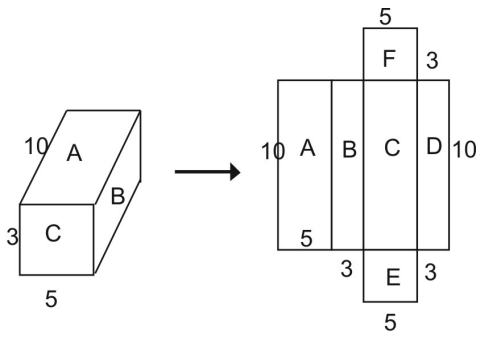
Från nätet kan du se att hela prismaets yta är lika med summan av de figurer som ingår i nätet:

Total yta = yta A + yta B + yta C + yta D + yta E + yta F

Med hjälp av formeln för arean av en rektangel kan du se att arean av rektangel A är:

A = l – w
A = 10 – 5 = 50 kvadratenheter

På samma sätt sätt sätts areorna för de andra rektanglarna in i ekvationen ovan.

Total yta = yta A + yta B + yta C + yta D + yta E + yta F
Total yta = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 3) + (5 – 3)
Total yta = 50 + 30 + 50 + 30 + 15 + 15
Total yta = 190 kvadratenheter

Exempel 3

Använd ett nät för att ta reda på prismaets yta.

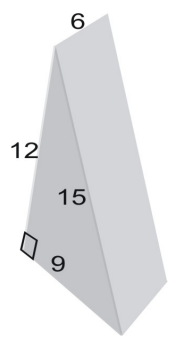
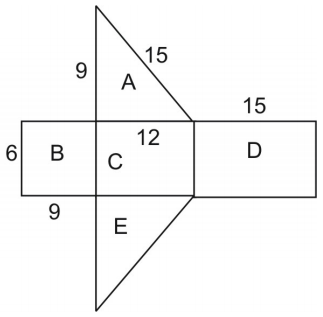
Nätets area är lika med figurens yta. För att hitta triangelns area använder vi formeln:

\displaystyle{A}=\frac{1}{2}hb\\\\\ där h är triangelns höjd och b är dess bas.

Notera att trianglarna A och E är kongruenta så vi kan multiplicera arean av triangel A med 2.

\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\\
\displaystyle\text{ }=2(\text{area }A)+\text{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\

Thus, är ytan 324 kvadratenheter.

Övningsuppgifter

För var och en av följande finner du ytan är a med hjälp av nätmetoden och omkretsen

  3. Basen på ett prisma är en rätvinklig triangel vars ben är 3 och 4 och visa höjd är 20. Vad är prismaets totala area?
  4. Ett högerhexagonalt prisma är 24 tum högt och har baser som är regelbundna hexagoner som mäter 8 tum på en sida. Vad är den totala ytan?
  5. Vad är volymen på prismat i problem 4?

I följande frågor är en lada formad som ett femkantigt prisma med måtten angivna i fot:

  1. Hur många kvadratfot (exklusive taket) finns det på ytan av den lada som ska målas?
  2. Om en gallon färg täcker 250 kvadratfot, hur många gallon färg behövs då för att måla ladan?
  3. En kartong är en perfekt kub med en kant som mäter 17 tum. Hur många kubikfot kan den rymma?
  4. En pool är 16 fot bred, 32 fot lång och jämnt 4 fot djup. Hur många kubikfot vatten kan den rymma?
  5. En spannmålslåda är 25 cm lång, 9 cm bred och 30 cm hög. Hur mycket flingor kan den rymma?

Svar

Nät och omkrets:

  1. 40,5 in2
  2. 838 cm2
  3. 252 kvadratenheter
  4. 1484.6 kvadratenheter
  5. 3990,7 kubikcentimeter

Ladan:

  1. 2450 kvadratfot
  2. 10 gallon färg
  3. 2,85 kubikfot (var försiktig här. Enheterna i problemet anges i tum men frågan frågar efter fot.)
  4. 2048 kubikfot
  5. 6750 cm3

Cylindrar

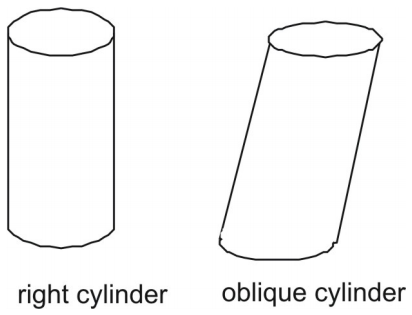
En cylinder är en tredimensionell figur med ett par parallella och kongruenta cirkulära ändar, eller baser. En cylinder har en enda böjd sida som bildar en rektangel när den ligger platt.

Som med prismor kan cylindrar vara rätvinkliga eller sneda. Sidan på en rät cylinder är vinkelrät mot dess cirkulära baser. Sidan på en sned cylinder är inte vinkelrät mot dess baser.

Surface Area of a Cylinder Using Nets

Du kan dekonstruera en cylinder till ett nät.

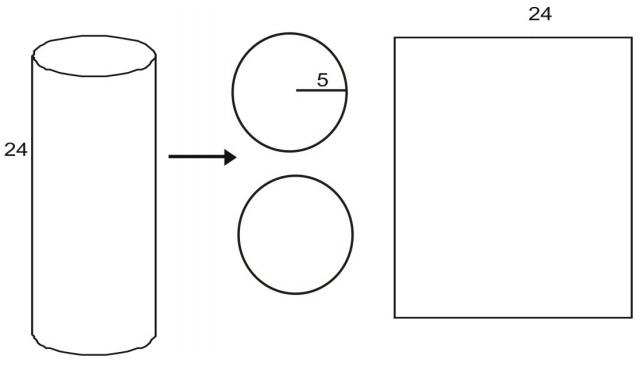
Området av varje bas ges av arean av en cirkel:

A=\pi{r}^2\\
A=\pi(5)^2\\\
A=25\pi\\\
A\approx(25)(3,14)=78,5\\\

Området av den rektangulära sidoytan L ges av produkten av bredd och höjd. Höjden är 24. Du kan se att ytans bredd är lika med den cirkulära basens omkrets.

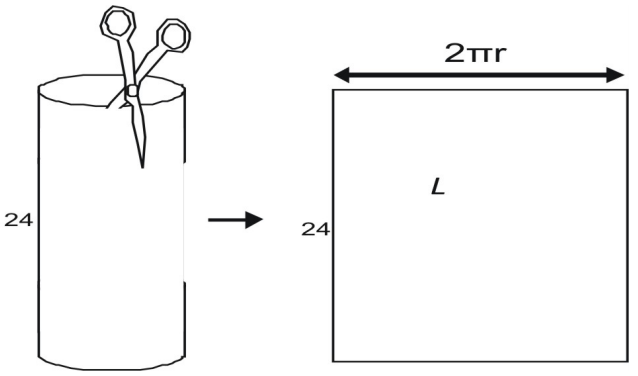
För att hitta bredden kan du tänka dig att du tar isär en burkliknande cylinder med en sax. När du klipper av sidoytan ser du att den är lika med omkretsen av burkens topp. Omkretsen av en cirkel ges av C = 2πr, den laterala arean, L, är

L=2{\pi}rh\\
L=2{\pi}(5)(24)\\
L=240\pi\\\
L\approx(240)(3.14)=753.6\\

Nu kan vi hitta arean av hela cylindern genom att använda A = (arean av två baser) + (arean av sidosidan).

A=2(75,36)+753,6\\
A=904,32\\

Du kan se att formeln som vi använde för att hitta den totala ytan kan användas för vilken rätvinklig cylinder som helst.

Arean av en rätvinklig cylinder: Du kan använda ett nät för att hitta cylinderns yta: Ytan av en högercylinder med radie och höjd h ges av A = 2B + L, där B är ytan av varje bas av cylindern och L är cylinderns sidoarea.

Exempel 4

Använd ett nät för att hitta cylinderns yta.

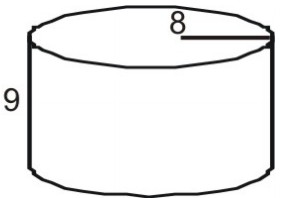
Rita och märk först ett nät för figuren.

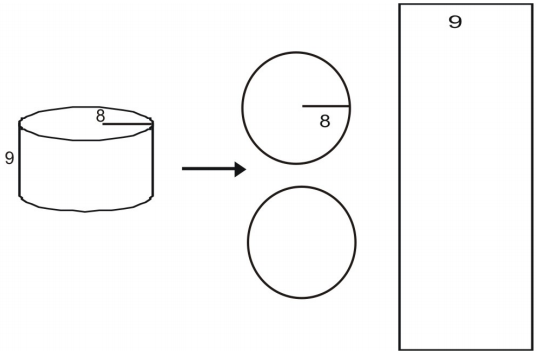
Beräkna arean för varje bas.

A=\pi{r}^2\\\
A=\pi(8)^2\\
A=64\pi\\
A\approx(64)(3.14)=200.96\\

Calculate L.

L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\\\

Finn arean av hela cylindern.

A=2(200.96)+452.16\\
A=854.08\\

Därmed är den totala ytan ungefär 854,08 kvadratenheter

Områdesarea av en cylinder med hjälp av en formel

Du har sett hur du kan använda nät för att hitta den totala ytan av en cylinder. Postulatet kan brytas ner för att skapa en allmän formel för alla rätvinkliga cylindrar.

A = 2B + L

Bemärk att basen, B, för en cylinder är: B = πr2

Den laterala arean, L, för en cylinder är:

L=\text{bredd av sidoarea}\cdot\text{höjd av cylinder}\\\
L=\text{omkrets av basen}\cdot\text{höjd av cylinder}\\\
L=2\pi{r}\cdot{h}\\

Sätter vi ihop de två ekvationerna får vi:

Om man räknar ut a från ekvationen får man:

Ytan av en rätcylindrig cylinder: En rätcylinder med radie r och höjd h kan uttryckas som:

A = 2πr2 + 2πrh

eller:

A = 2πr(r + h)

Du kan använda formlerna för att hitta arean av en rätcylinder.

Exempel 5

Använd formeln för att hitta cylinderns yta.

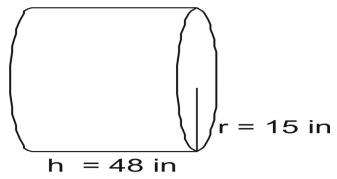
Skriv formeln och sätt in värdena och lös.

A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ kvadratcentimeter}\\\

Exempel 6

Hitta cylinderns yta.

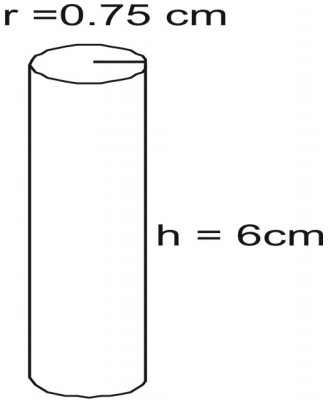
Skriv formeln och sätt in värdena och lös.

A=2\pi{r}(r+h)\\
A=2(3,14)(0,75)\\
A=31.7925\text{ kvadratcentimeter}\\\

Exempel 7

Hitta höjden på en cylinder som har radie 4 cm och en yta på 226,08 kvadratcentimeter.

Skriv formeln med den givna informationen och lös h.

A=2\pi{r}(r+h)\\
226,08=2(3,14)(4)\\
226,08=25,12\\
226,08=100,48+25,12h\\
5=h\\\

Sfärer

En sfär är en tredimensionell figur som har formen av en boll.

Sfärer kan karaktäriseras på tre sätt.

  • En sfär är mängden av alla punkter som ligger på ett fast avstånd r från en enda centrumpunkt O.
  • En sfär är den yta som uppstår när en cirkel roteras runt någon av dess diametrar.

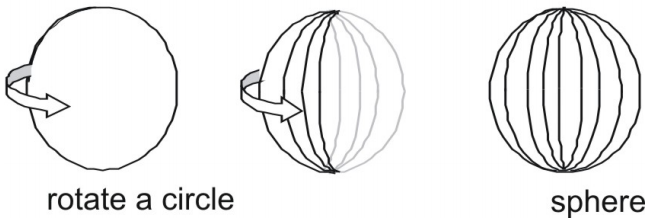
Områdesarea av en sfär

Du kan härleda formeln för en sfärs yta genom att göra mätningar av sfärer och cylindrar. Här visar vi en sfär med en radie på 3 och en högercylinder med både en radie och en höjd på 3 och uttrycker arean i termer av π.

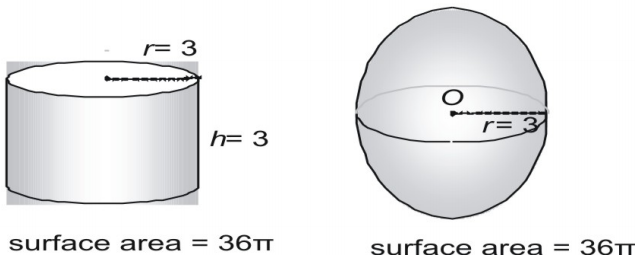
Prova nu ett större par och uttrycka arean i decimalform.

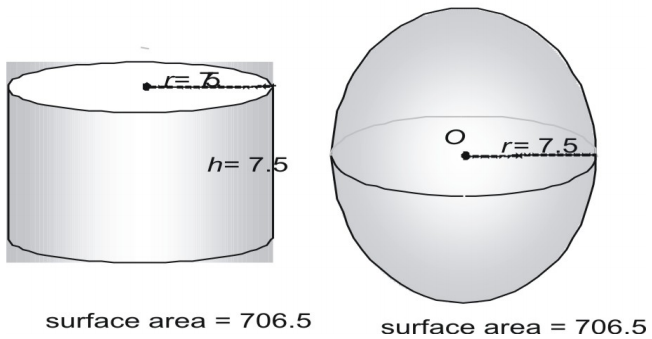
Se på ett tredje par.

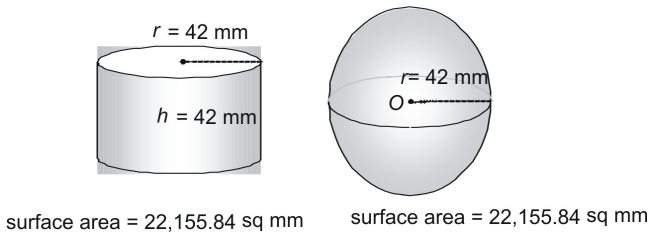
Är det en slump att en sfär och en cylinder vars radie och höjd är lika med sfärens radie har exakt samma yta? Inte alls! Faktum är att de gamla grekerna använde en metod som visade att följande formel kan användas för att hitta ytan av en sfär (eller en cylinder i vilken ).

Ytan av en sfär ges av: A = 4πr2

Exempel 8

Hitta ytan på en sfär med en radie på 14 fot.

Använd formeln.

A=4\pi{r}^2\\
A=4\pi(14)^2\\
A=4\pi(14)^2\\
A=4\pi(196)\\
A=784\pi\\
2461.76\text{ kvadratfot genom att använda }3.14\text{ för }\pi\\\\

Exempel 9

Hitta ytan på följande figur med hjälp av π.

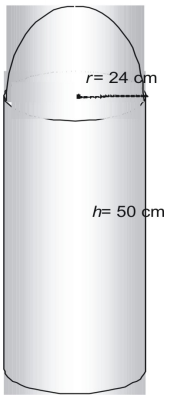
Figuren består av en halv sfär eller halvklot och en cylinder utan topp.

A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half sfär})=2\pi(576)\\
A(\text{halv sfär})=1152\pi\text{ kvadrat cm}\\

Olika nu arean av cylindern utan dess topp.

A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\

Thus, är den totala ytan 1152\pi+2976\pi=4128\pi\\\

Övningsuppgifter

  1. Finn radien på den sfär som har en volym på 335 cm3.
  2. Bestäm ytan och volymen för denna form:
  3. Radien för en sfär är 4. Bestäm dess volym och totala yta.
  4. En sfär har en radie på 5. En rät cylinder som har samma radie har samma volym. Hitta cylinderns höjd och totala yta.
  5. Sfär: volym = 296 cm3. Hitta diametern.
  6. Sfär: ytan är 179 in2. Hitta radien.
  7. Tennisbollar med en diameter på 3,5 tum säljs i burkar om tre stycken. Burken är en cylinder. Anta att bollarna rör vid burken på sidorna, toppen och botten. Vad är volymen på det utrymme som inte upptas av tennisbollarna?
  8. En sfär har en yta på 36π in2. Hitta dess volym.
  9. En gigantisk skopa, som manövreras av en kran, har formen av en halvklot med radie = 21 tum. Skopan är fylld med smält hett stål. När stålet hälls i en cylindrisk lagringstank som har en radie på 28 tum kommer det smälta stålet att stiga till en höjd av hur många tum?

Svar

Observera att man i dessa problem använder π och inte 3,14.

  1. 1. Radius = 4,31 cm
  2. Områdesarea = 706,86 cm2
    Volym = 1767,15 cm3
  3. Volym = 268,08 enheter3
    Områdesarea = 201,06 enheter2
  4. Höjd = 20/3 enheter total yta = 366,52 enheter2
  5. Diameter = 8,27cm
  6. Radius = 3.77 tum
  7. Cylindervolym = 32,16π in3 volym av tennisbollar = 21,44π in3
    Volym av utrymme som inte upptas av tennisbollar = 33,68 in3
  8. Volym = 113,10 in3
  9. Höjden på det smälta stålet i cylindern blir 7,88 tum

.

Lämna ett svar

Din e-postadress kommer inte publiceras.