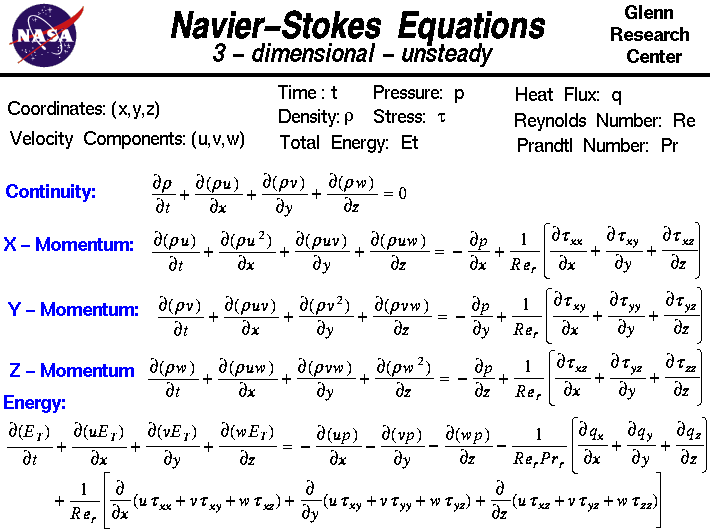
På denna bild visar vi den tredimensionella instabila formen av Navier-Stokes ekvationer.Dessa ekvationer beskriver hur hastigheten, trycket, temperaturen och densiteten hos en rörlig vätska hänger samman.Ekvationerna togs fram oberoende av varandra av G.G. Stokes i England och M. Navier i Frankrike i början av 1800-talet.Ekvationerna är en utvidgning av Euler-ekvationerna och inkluderar viskositetens effekter på flödet.Ekvationerna är mycket komplexa, men ingenjörsstudenter lär sig ändå att härleda dem genom en process som liknar den härledning som vi presenterar på webbsidan för bevarande av rörelsemängd.
Ekvationerna är en uppsättning kopplade differentialekvationer och skulle i teorin kunna lösas för ett givet flödesproblem med hjälp av metoder från kalkyl.Men i praktiken är dessa ekvationer för svåra att lösa analytiskt.Förr gjorde ingenjörer ytterligare approximationer och förenklingar av ekvationerna tills de hade en grupp ekvationer som de kunde lösa.På senare tid har höghastighetsdatorer använts för att lösa approximationer av ekvationerna med hjälp av olika tekniker, t.ex. finita differens-, finitvolym-, finita element- och spektralmetoder.Detta studieområde kallas Computational Fluid Dynamics eller CFD.
Navier-Stokes ekvationer består av en tidsberoende kontinuitetsekvation för bevarande av massa, tre tidsberoende momentbevarandeekvationer och en tidsberoende energibesparingsekvation.Det finns fyra oberoende variabler i problemet, de rumsliga koordinaternax, y och z för en viss domän och tiden t. Det finns sex beroende variabler: trycket p, densiteten r och temperaturen T (som ingår i energidekvationen genom den totala energin Et) och tre komponenter av hastighetsvektorn: u-komponenten i x-led, v-komponenten i y-led och w-komponenten i z-led.Alla de beroende variablerna är funktioner av alla fyra oberoende variabler.Differentialekvationerna är därför partiella differentialekvationeroch inte de vanliga differentialekvationer som du studerar i en begynnande kalkylkurs.
Du kommer att märka att differentialsymbolen skiljer sig från de vanliga ”d /dt” eller ”d /dx” som du ser för vanliga differentialekvationer. Symbolen ”
” används för att ange partiella derivata.Symbolen anger att vi ska hålla alla oberoende variabler fasta, utom variabeln bredvid symbolen, när vi beräknar en derivata. Ekvationerna är:
Kontinuitet: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Moment: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Moment: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energi: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
där Re är Reynolds tal som är en likhetsparameter som är förhållandet mellan skalningen av flödets tröghet och de viskösa krafterna i flödet. Variablerna q är värmeflödeskomponenterna och Pr är Prandtltalet som är en likhetsparameter som är förhållandet mellan de viskösa spänningarna och de termiska spänningarna.Variablerna tau är komponenter av spänningstensorn.En tensor skapas när man multiplicerar två vektorer på ett visst sätt. Vår hastighetsvektor har tre komponenter; spänningensorn har nio komponenter. Varje komponent i spänningstenorn är i sig själv en andra derivat av hastighetskomponenterna.
Termerna på vänster sida av impulsekvationerna kallas för ekvationernas konvektionstermer.Konvektion är en fysisk process som sker i ett gasflöde där en viss egenskap transporteras genom den ordnade rörelsen i flödet.De termer på högra sidan av impulsekvationerna som multipliceras med det omvända Reynoldstalet kallas diffusionstermer.Diffusion är ett fysikalisk process som sker i ett gasflöde där någon egenskap transporteras genom gasmolekylernas slumpmässiga rörelse.Diffusionen är relaterad till spänningensorn och gasens viskositet. Turbulens och bildandet av gränsskikt är ett resultat av diffusion i flödet. Eulers ekvationer innehåller endast konvektionstermerna i Navier-Stokes ekvationer och kan därför inte modellera gränsskikt. Det finns en särskild förenkling av Navier-Stokesekvationerna som beskriver gränsskiktsflöden.
Bemärk att alla beroende variabler förekommer i varje ekvation.För att lösa ett flödesproblem måste man lösa alla fem ekvationer samtidigt; det är därför vi kallar detta för ett kopplat ekvationssystem.Det finns faktiskt några andraekvationer som krävs för att lösa detta system. Vi visar bara fem ekvationer för sex okända. En tillståndsekvation relaterar gasens tryck, temperatur och densitet.Och vi måste specificera alla termer i spänningensorn.I CFD approximeras ofta spänningensorn-termerna av en turbulensmodell.
Aktiviteter:
Guidade turer
Navigation ..
Begynnelsehandbok Home Page