Sun, 18 Jun 2006
1+1=2
Whitehead och Russells Principia Mathematica är berömda för att det tar tusen sidor att bevisa att 1+1=2. Naturligtvis bevisar den en massa andra saker också. Om de hade velat bevisa endast att 1+1=2 skulle det förmodligen ha tagit hälften så mycket plats.
Principia Mathematica är en märklig bok som är värd att titta närmare på både ur historisk och matematisk synvinkel. Den skrevs omkring 1910, och den matematiska logiken var då fortfarande i sin linda, nyss förädlad efter den omvandling som Peano och Frege hade gjort av den. Notationen är något oklar, eftersom den matematiska notationen har utvecklats avsevärt sedan dess. Och många av de enkla tekniker som vi nu tar för givna saknas.Likt ett dåligt skrivet datorprogram är en stor del av Principia Mathematicas volym upprepad kod, separata avsnitt som i huvudsak säger samma saker, eftersom författarna ännu inte har lärt sig de tekniker som skulle göra det möjligt att kombinera dessa avsnitt till ett enda.
Till exempel börjar avsnitt ∗22, ”Calculus of Classes”, med att definiera undergruppsrelationen (∗22.01) och operationerna för mängdunion och mängdsnitt (∗22.02 och .03), komplementet till en mängd (∗22.04) och skillnaden mellan två mängder (∗22.05). Därefter bevisas kommutativitet och associativitet för sammanslagning och intersektion av mängder (∗22.51, .52, .57 och .7), olika egenskaper som !!\alpha\cap\alpha = \alpha!!! (∗22.5) och liknande, och arbetar sig fram till satser som ∗22.92: !!\alpha\subset\beta \rightarrow \alpha\cup(\beta -\alpha)!!!.
Avsnitt ∗23 är ”Relationsberäkning” och börjar på nästan exakt samma sätt, genom att definiera subrelationsrelationen (∗23.01), och operationerna för relationell förening och skärning (∗23.02 och .03), komplementet till en relation (∗23.04) och skillnaden mellan två relationer (∗23.05). Itlater bevisar kommutativiteten och associativiteten hos relationell union och intersektion (∗23.51, .52, .57 och .7), olika egenskaper som !!\alpha\dot\cap\alpha = \alpha!!! (∗22.5) och liknande, och arbetar sig fram till satser som ∗23.92: !!\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot-\alpha)!!!.
Avsnittet ∗24 handlar om existensen av uppsättningar, nolluppsättningen !!\Lambda!!, den universella uppsättningen !!{\rm V}!!!, deras egenskaper och så vidare, och sedan dupliceras avsnitt ∗24 i ∗25 i en serie satser om existensen av relationer, nollrelationen !!\dot\Lambda!!, den universella relationen !!\dot {\rm V}!!, deras egenskaper och så vidare.
Det var så Whitehead och Russell gjorde det 1910. Hur skulle vi göra det idag? En relation mellan S och T definieras som en delmängd avS × T och är därför en mängd. Union, intersektion, skillnad och de andra operationerna är precis samma för relationer som för uppsättningar, eftersom relationer är uppsättningar. Alla satser om unioner och skärningar av relationer, som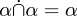 
, försvinner helt enkelt, eftersom vi redan har bevisat dem för uppsättningar och relationer är uppsättningar. Nollrelationen är nollmängden. Den universella relationen är den universella mängden.
En enorm mängd annat maskineri försvinner 2006 på grund av föreningen av relationer och mängder. Principia Mathematica behöver en särskild notation och en särskild definition för resultatet av att begränsa en relation till de par vars första element ingår i en viss mängd S, eller vars andra element ingår i S, eller vars båda element ingår i S. År 2006 skulle vi bara använda den vanliga mängdintersektionsoperationen och tala om R ∩(S×B) eller liknande.
Whitehead och Russell kunde inte göra detta 1910 eftersom en viktig del av maskineriet saknades: det ordnade paret. År 1910 visste ingen hur man skulle bygga ett ordnat par av bara logik och mängder. År 2006 (eller till och med 1956) skulle vi definiera det ordnade paret <a, b> som mängden {{a}, {a, b}}. Sedan skulle vi visa som ett teorem att <a, b> = <c, d> om och endast om a=c och b=d, med hjälp av egenskaper hos mängder. Därefter skulle vi definiera A×B som mängden av alla p så att p = <a,b> ∧ a ∈ A ∧ b∈ B. Därefter skulle vi definiera en relation mellan mängderna A och B som en delmängd av A×B. Då skulle vi få alla ∗23 och ∗25 och en hel del ∗33 och ∗35 och ∗36 gratis, och förmodligen en hel del annat också.
(Förresten uppfanns {{a}, {a, b}} av Kuratowski. Det brukar tillskrivas Norbert Wiener, menWieners idé, även om den är likartad, var faktiskt mer komplicerad.)
Det finns inga ordnade par i Principia Mathematica,utom underförstått. Det finns knappt ens några uppsättningar. Whitehead ochRussell vill basera allt på logik. För Whitehead och Russell är det grundläggande begreppet ”propositionell funktion”, vilket är en funktion φ vars utgång är ett sanningsvärde. För varje sådan funktion finns det en motsvarande mängd, som de betecknar med !!\hat x\phi(x)!!, mängden av alla x så att φ(x) är sann. För Whitehead och Russell är en arelation implicerad av en propositionsfunktion av två variabler, på samma sätt som en mängd impliceras av en propositionsfunktion av en variabel. År 2006 avstår vi från ”funktioner med två variabler” och talar bara om funktioner vars (enda) argument är ett ordnat par; en relation blir då mängden av alla ordnade par för vilka en funktion är sann.
Russell ska ha sagt att upptäckten av Shefferstroke (en enda logisk operatör från vilken alla andra logiska operatörer kan byggas upp) var ett enormt framsteg, och att det skulle förändra allting. Detta verkar konstigt för oss nu, eftersom upptäckten av Sheffer-slaget verkar så enkelt, och det förändrar egentligen ingenting viktigt. Man behöver bara lägga till en anteckning i början av kapitel 1 som säger att ∼p och p∨q är förkortningar för p|p respektive p|p.|.q|q, bevisa de fem grundläggande axiomen och lämna allt annat oförändrat. Men Russell skulle med viss rättvisa ha kunnat säga samma sak om upptäckten att ordnade par kan tolkas som mängder, en enkel upptäckt som verkligen skulle ha förvandlat Principia Mathematica till ett helt annat verk.
Hursomhelst, med den bakgrunden på plats kan vi diskutera Principia Mathematicas bevis för 1+1=2. Detta sker ganska sent i Principia Mathematica, i avsnitt ∗102. Min förkortade version går bara till ∗56, men det är tillräckligt långt för att komma till den viktiga föregångssatsen, ∗54.43, som skannas nedan:
Notationen kan vara överväldigande, så vi koncentrerar oss bara på uttalandet av satsen och struntar i allt annat, till och med i den hjälpsamma anmärkningen längst ner:
Detta är satsen som bevisas; det som följer är beviset.
Nu ska jag förklara notationen, som har förändrats något sedan 1910. För det första använder Principia Mathematica Peanos notation med ”prickar” för att särskilja prejudikat, medan vi nu använder parenteser i stället. Punktnotationen kräver en viss tillvänjning, men har några tydliga fördelar jämfört med parenteser. Tanken är bara att man anger gruppering genom att sätta in punkter, så att (1+2)×(3+4)& gånger(5+6) skrivs som1+2.×.3+4.×.5+6. Den mellersta delformeln står mellan ett par punkter. Underformeln (1+2) ligger också mellan ett par punkter, men punkten på vänster sida är överflödig och vi utelämnar den; på samma sätt avgränsas underformeln (5+6) av en punkt på vänster sida och av slutet av formeln på höger sida.
Hur gör man om man behöver nästla in parenteser? Då använder du fler punkter. En dubbel punkt (:) är som en enkel punkt, men starkare. Vi skriver till exempel ((1+2)×3)+4 som 1+2 . × 3 : + 4, och den dubbla punkten isolerar hela 1+2 . × 3 uttrycket till en enkel underformel som +4 gäller för.
Ibland behöver man fler nivåer av företräde, och då använder man trepunkt (.: och :.) och fyrpunkt (::). Den här formeln har, som du ser, dubbla och tredubbla punkter. Om vi översätter prickarna till standardparentesnotering får vi $$$\ast54,43. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$$. Detta ser mer rörigt ut än versionen med prickar, och i okomplicerade formler kan det vara svårt att räkna ut vilka parenteser som passar ihop med vilka. Med prickarna är det alltid enkelt. Så jag tycker att det är lite olyckligt att denna konvention inte längre används.
Symbolen !!\vdash!! har inte ändrats; den betyder att den formel som den gäller för påstås vara sann. !!\supset!! är logisk implikation, och !!\equiv!! är logisk ekvivalens. Λ är den tomma mängden, som vi numera skriver ∅. ∩ ∪ och ∈ har sina moderna betydelser: ∩ och ∪ är operatörerna set intersection och union, och x∈y betyder att x är ett element i set y.
De återstående punkterna är semantiska. α och β är mängder. 1betecknar mängden av alla mängder som har exakt ett element. Det vill säga det är mängden { c : det finns a så att c = {a } }. Satser om 1 inkluderar till exempel:
- att Λ∉1 (∗52.21),
- att om α∈1 så finns det ett visst x så att α ={x} (∗52.1), och
- att {x}∈1 (∗52.22).
2 är på samma sätt mängden av alla mängder som har exakt två element. En viktig sats om 2 är ∗54.3, som säger $$\ast54.3. \vdash 2 = \hat\alpha\{ (\exists x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\in 1 \}.$$$I Principia Mathematicas notation skrivs {x}, den mängd som innehåller x och inget annat, ι’x, så denna sats säger att 2 är identisk med mängden av alla α så attα har något element x , som, när det avlägsnas från α, lämnar kvar en mängd med 1 element.
Här är alltså satsen ∗54.43 igen:
Det hävdas att om mängderna α och β vardera har exakt ett element, så är de disjunkta (det vill säga har inga element gemensamt) om och endast om deras förening har exakt två element.
Beviset, som visas i skanningen ovan efter ordet ”Dem.” (förkortning för ”demonstration”) lyder så här:
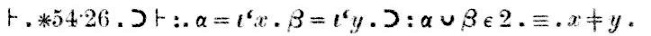
”Theorem ∗54.26implies that if α = {x} and β = {y}, thenα∪β has 2 elements if and only if x isdifferent from y.”
”Enligt satsen ∗51.231 är den sista biten (x skiljer sig fråny) sann om och endast om {x} och {y} är disjunkna.”
”Enligt ∗13.12 är den här sista biten ({x} och {y} är disjokt) sann om och endast om α och β själva är disjokt.” Den partiella slutsatsen vid denna punkt,som är märkt (1), är att om α = {x} och β ={y}, så är α∪β ∈ 2 om och endast omα∩β = Λ.
Beviset fortsätter: ”Slutsats (1), med satser ∗11.11 och ∗11.35,innebär att om det finns x och y så att α är{x} och β är {y}, då α∪β ∈ 2om och endast om α och β är disjunkna.” Denna slutsats är märkt med (2).
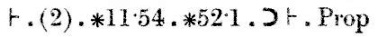
Slutligt innebär slutsatsen (2), tillsammans med satserna ∗11.54 och ∗52.1,den sats som vi försökte bevisa.
Kanske är det man ska lägga märke till här hur mycket små stegen är. ∗54.26, som denna sats är starkt beroende av, är nästan densamma; den hävdar att {x}∪{y} ∈ 2 om och endast om x≠y. ∗54.26 beror i sin tur på ∗54.101, som säger att α har 2 element om och endast om det finns x ochy, som inte är desamma, så att α = {x} ∪{y}. ∗54.101 skiljer sig bara en liten bit från definitionen av 2. Sats ∗51.231 säger att {x} och {y} är disjoina om och endast om x och y är olika.∗52.1 är en grundläggande egenskap hos 1; vi har sett den tidigare.
De andra satser som citeras i demonstrationen är mycket små tekniska frågor. ∗11.54 säger att man kan ta ett påstående om att två saker existerar och dela upp det i två påståenden, där vart och ett påstår att en av sakerna existerar. ∗11.11 är ännu smalare: den säger att om φ(x, y) alltid är sant, så kan man bifoga en universell kvantifierare och hävda att φ(x, y) är sant för alla x och y. ∗13.12 handlar om substitution av lika för lika: om x och y är lika, så har x en egenskap ψ om och endast om y också har det.
Jag har inte sett de senare delarna av Principia Mathematica, eftersom mitt exemplar slutar efter avsnitt ∗56, och de aritmetiska sakerna är mycket senare. Men den här satsen har klart och tydligt betydelsen av 1+1=2 i sig, och den senare satsen (∗110.643)som faktiskt hävdar 1+1=2 är starkt beroende av den här satsen.
Och även om jag inte är helt säker på vad som kommer att hända senare (jag har slösat alldeles för mycket tid på detta redan för att lägga ner mer tid på att få den fullständiga versionen från biblioteket) kan jag göra en kvalificerad gissning. Principia Mathematica kommer att definiera talet 17 som mängden av alla mängder med 17 element, och på samma sätt för alla andra tal. Användningen av symbolen 2 för att representera mängden av alla mängder med 2 element förebådar detta. Dessa uppsättningar av alla uppsättningar av en viss storlek kommer sedan att identifieras som ”kardinaltalen”.
Principia Mathematica kommer att definiera summan av kardinaltalen p och q på följande sätt: ta en representativ mängd från p; a har p element. Ta en representativ mängd bfrån q; b har q element. Låt c =a∪b. Om c ingår i något kardinaltal r, och om a och b är odelade, så är summan av p och q r.
Med denna definition kan du bevisa de vanliga önskvärda egenskaperna hos addition, såsom x + 0 = x, x + y = y + x och 1 + 1 = 2.
I synnerhet följer 1+1=2 direkt av satsen ∗54.43; det är precis vad vi vill ha, för för att beräkna 1+1 måste vi hitta två disjunkta representanter för 1 och ta deras förening; ∗54.43 hävdar att föreningen måste vara ett element i 2, oavsett vilka representanter vi väljer, så att 1+1=2.
Post scriptum: Peter Norvig säger att omflexen iPrincipia Mathematica-notationen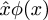 
är den yttersta källan till användningen av ordetlambda för att beteckna en anonym funktion i programspråken Lisp och Python. Ni vet säkert att dessa språk har fått ”lambda” från Alonzo Churchs användning av den grekiska bokstaven λ för att representera funktionsabstraktion i sin ”λ-kalkyl”: I Lisp är(lambda (u) B) en funktion som tar ett argumentu och returnerar värdet av B; i λ-kalkylen är λu.B en funktion som tar ett argumentu och returnerar värdet av B. Norvig säger att Church ursprungligen planerade att skriva funktionenλu.B som û.B, men hans skrivare klarade inte av att göra circumflexa accenter. Så han övervägde att flyttacirkumflexen till vänster och använda ett stort lambda i stället:Λu.B. Det stora Λ såg för mycket ut somelogiskt och ∧, vilket var förvirrande, så han använde istället lambdaλ med små bokstäver.
Post post scriptum: Alla säger alltid ”Russell och Whitehead”.Googleresultaten för ”Russell och Whitehead” överträffar till exempel resultaten för ”Whitehead och Russell” med två gånger så mycket som de för ”Whitehead och Russell”. Varför? På omslaget och titelsidan står det ”Alfred North Whitehead och Bertrand Russell, F.R.S.”. Hur och när förlorade Whitehead sin första plats?
permanent länk