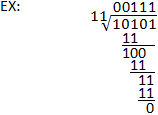Brug følgende regnemaskiner til at foretage addition, subtraktion, multiplikation eller division af to binære værdier samt til at konvertere binære værdier til decimale værdier og omvendt.

Binær beregning – tilføjelse, subtraktion, multiplikation, eller dividere
Konverter binær værdi til decimalværdi
Konverter decimalværdi til binær værdi
Relateret Hex Calculator | IP Subnet Calculator
Det binære system er et numerisk system, der fungerer stort set identisk med det decimaltalsystem, som folk sandsynligvis er mere bekendt med. Mens det decimale talsystem bruger tallet 10 som sin base, bruger det binære system 2. Desuden bruger det decimale system cifrene 0 til 9, mens det binære system kun bruger 0 og 1, og hvert ciffer betegnes som en bit. Bortset fra disse forskelle beregnes operationer som f.eks. addition, subtraktion, multiplikation og division efter de samme regler som i decimalsystemet.
Næsten al moderne teknologi og computere anvender det binære system på grund af dets lette implementering i digitale kredsløb ved hjælp af logiske gates. Det er meget enklere at konstruere hardware, der kun skal registrere to tilstande, tændt og slukket (eller sandt/falsk, til stede/fraværende osv.). Hvis man anvender et decimalsystem, vil det kræve hardware, der kan registrere 10 tilstande for cifrene 0 til 9, og det er mere kompliceret.
Nedenfor er der nogle typiske konverteringer mellem binære og decimale værdier:
Binær/Decimal konvertering
| Decimal | Binary | Binary |
| 0 | 0 | 0 |
| 1 | 1 | |
| 2 | 10 | |
| 3 | 11 | |
| 4 | 100 | |
| 7 | 111 | |
| 8 | 1000 | |
| 10 | 1010 | |
| 16 | 10000 | |
| 20 | 10100 |
Mens det kan virke forvirrende at arbejde med binært i starten, bør forståelsen af, at hver binær pladsværdi repræsenterer 2n, ligesom hver decimalplads repræsenterer 10n, hjælpe med at skabe klarhed. Tag f.eks. tallet 8. I det decimale talsystem er 8 placeret på den første decimalplads til venstre for decimalpunktet, hvilket betegner 100-pladsen. Det betyder i bund og grund:
8 × 100 = 8 × 1 = 8
Med tallet 18 til sammenligning:
(1 × 101) + (8 × 100) = 10 + 8 = 18
I binært tal repræsenteres 8 som 1000. Når man læser fra højre til venstre, repræsenterer det første 0 20, det andet 21, det tredje 22 og det fjerde 23; ligesom i decimalsystemet, blot med en base på 2 i stedet for 10. Da 23 = 8, indtastes en 1 på denne plads, hvilket giver 1000. Med 18 eller 10010 som eksempel:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Den trinvise proces for at konvertere fra det decimale til det binære system er:
- Find den største potens af 2, der ligger inden for det givne tal
- Træk denne værdi fra det givne tal
- Find den største potens af 2 inden for den rest, der blev fundet i trin 2
- Gentag det igen, indtil der ikke er nogen rest
- Indtast en 1 for hver binær pladsværdi, der blev fundet, og et 0 for resten
Med målet på 18 igen som eksempel er der nedenfor en anden måde at visualisere dette på:
| 2n | 24 | 23 | 22 | 21 | 20 | ||
| Indhold inden for 18 | 1 | 1 | 0 | 0 | 1 | 0 | |
| Mål: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||||
Konverteringen fra det binære til det decimale system er enklere. Bestem alle de stedværdier, hvor 1 forekommer, og find summen af værdierne.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 | |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Heraf: 16 + 4 + 2 + 1 = 23.
Binær addition
Binær addition følger de samme regler som addition i decimalsystemet, bortset fra, at i stedet for at overføre en 1, når de adderede værdier er lig med 10, sker overførslen, når resultatet af additionen er lig med 2. Se eksemplet nedenfor for at få en tydeliggørelse.
Bemærk, at i det binære system:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, overføres 1’eren, dvs. 10
EX:
| 10 | 11 | 11 | 10 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | ||
| = | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Den eneste reelle forskel mellem binær og decimal addition er, at værdien 2 i det binære system svarer til 10 i det decimale system. Bemærk, at de overstregede 1’er repræsenterer cifre, der overføres. En almindelig fejl, som man skal være opmærksom på, når man udfører binær addition, er i det tilfælde, hvor 1 + 1 = 0 også har en 1, der er overført fra den foregående kolonne til højre for den. Værdien nederst bør i så fald være 1 fra den overførte 1 i stedet for 0. Dette kan observeres i den tredje kolonne fra højre i ovenstående eksempel.
Binær subtraktion
Som ved binær addition er der ikke meget forskel på binær og decimal subtraktion, bortset fra de forskelle, der opstår ved kun at bruge cifrene 0 og 1. Lån forekommer i alle tilfælde, hvor det tal, der subtraheres, er større end det tal, det subtraheres fra. Ved binær subtraktion er det eneste tilfælde, hvor det er nødvendigt at låne, når 1 trækkes fra 0. Når dette sker, bliver 0 i den kolonne, der lånes, i princippet til “2” (0-1 ændres til 2-1 = 1), mens 1 i den kolonne, der lånes fra, reduceres med 1. Hvis den efterfølgende kolonne også er 0, skal der lånes fra hver efterfølgende kolonne, indtil en kolonne med værdien 1 kan reduceres til 0. Se eksemplet nedenfor for at få en forklaring.
Bemærk, at i det binære system:
- 0 – 0 = 0
0 – 1 = 1, lån 1, hvilket resulterer i -1, der overføres
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | |||
| – | 0 | 1 | 1 | 0 | 1 | ||
| = | 0 | 1 | 0 | 1 | 0 | ||
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Bemærk, at de viste superskripter er de ændringer, der sker for hver bit, når der lånes. Den kolonne, der lånes, får i det væsentlige 2 ved at låne, og den kolonne, der lånes fra, reduceres med 1.
Binær multiplikation
Binær multiplikation er uden tvivl enklere end dens decimale modstykke. Da de eneste værdier, der anvendes, er 0 og 1, er de resultater, der skal lægges sammen, enten det samme som den første term eller 0. Bemærk, at der i hver efterfølgende række skal lægges 0’er som pladsholdere, og værdien skal forskydes til venstre, ligesom ved decimalmultiplikation. Kompleksiteten i binær multiplikation skyldes en kedelig binær addition, der afhænger af, hvor mange bits der er i hver term. Se eksemplet nedenfor for at få en forklaring.
Bemærk, at i det binære system:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Som det fremgår af eksemplet ovenfor, er processen ved binær multiplikation den samme som ved decimalmultiplikation. Bemærk, at 0-placeholderen er skrevet i den anden linje. Typisk er 0-placeholderen ikke visuelt til stede i decimalmultiplikation. Selv om det samme kan gøres i dette eksempel (med 0-placeholderen antaget i stedet for eksplicit), er den medtaget i dette eksempel, fordi 0’et er relevant for enhver binær regnemaskine til binær addition/subtraktion, som den, der findes på denne side. Hvis 0’et ikke blev vist, ville det være muligt at begå den fejl at udelukke 0’et, når man adderer de binære værdier, der er vist ovenfor. Bemærk igen, at i det binære system er ethvert 0 til højre for et 1 relevant, mens ethvert 0 til venstre for det sidste 1 i værdien ikke er det.
EX:
- 1 0 1 0 1 1 1 0 0 0
= 0 0 1 0 1 0 1 1 1 0 0 0
≠ 1 0 1 0 1 0 1 1 0 0 0 0 0 0
Binær division
Den binære division foregår på samme måde som den lange division i decimalsystemet. Dividenden divideres stadig med divisoren på samme måde, med den eneste væsentlige forskel er brugen af binær subtraktion i stedet for decimal subtraktion. Bemærk, at det er vigtigt at have en god forståelse af binær subtraktion for at gennemføre binær division. Se eksemplet nedenfor samt afsnittet om binær subtraktion for at få en uddybning.