
Fern
Her er et nyt spørgsmål fra læseren Pehr i Sverige:
Hej,
Først af alt, vidunderlig hjemmeside. Elsker det.
Jeg har studeret afsnittet om polarkoordinater i håb om at udvide min viden om den ligebenede spiral. De interaktive værktøjer er fantastiske, selv om jeg har svært ved at udlede den nøjagtige matematiske løsning på, hvorfor den resulterende funktion for den gyldne spiral er
r = ae^(b(theta))
For lidt baggrund for Pehrs spørgsmål, se:
Polære koordinater, kurver i polære koordinater og ækvovangulær spiral
Spiraler er almindelige i naturen og har inspireret matematikere i århundreder.

Aloe-spiral

Spiral-galaksen NGC 5194
Logaritmiske spiraler
Den gyldne spiral, som Pehr spørger om, er et specialtilfælde af den logaritmiske spiral.
Logaritmiske spiraler vokser således, at vinklen på en linje fra spiralens centrum til tangenten til kurven i det pågældende punkt er konstant. Derfor er de også kendt som “ligevinklede” spiraler.
For at se, hvad det betyder, er de 3 spidse vinkler, der er markeret i det følgende bregnebillede, ca. 80°

Quei-vinklet bregne
Vi bruger normalt funktioner i polære koordinater, når vi beskriver spiraler. Hvis vi ellers bruger almindelige rektangulære koordinater, bliver formlerne meget komplekse.
Formlen for en logaritmisk spiral ved hjælp af polarkoordinater er:
r = aeθ cot b
hvor
r er afstanden fra oprindelsen (eller “polen”)
a er en konstant
θ er vinklen (i radianer) fra den vandrette akse. Så koordinaterne for et punkt på kurven i polarkoordinater er givet ved (r, θ).
b er den vinkel (i radianer – den “lige” vinkel), som linjen fra spiralens centrum danner med tangenten til spiralen. I bregnetilfældet ovenfor er b ≈ 1,4 radianer (≈ 80°).
Som følge af den måde, vi definerede den logaritmiske spiral på, er forholdet mellem afstandene fra centrum til hver spiralarm i et tilstødende par konstant.

Spiralarmene i et konstant forhold
Forholdet
afstand til den første arm: afstand til den anden arm
= 29:69
≈ 0.42
Det andet forhold
afstanden til anden arm: afstand til tredje arm
= 69:154
≈ 0,45
Vi ser, at forholdene er næsten ens. (I en egentlig logaritmisk spiral er de præcis de samme. Det er ikke en eksakt videnskab at vælge startpunktet for bregnen!)
Den gyldne spiral
Den gyldne spiral er et specialtilfælde af den logaritmiske spiral.
Vi kan skrive den generelle logaritmiske spiral som en funktion i polære koordinater ved hjælp af t på følgende måde:
r(t) = aet cot b
Bemærk: Normalt bruger vi θ for den uafhængige variabel, men vi bruger ofte t, da vi kan tænke på, at spiralen bliver tracket ud over tid. Desuden er det nemmere at skrive!
Den gyldne spiral har den særlige egenskab, at for hver 1/4 omdrejning (90° eller π/2 i radianer) øges afstanden fra spiralens centrum med det gyldne snit φ = 1,6180.
For at dette kan ske, skal cot b antage den værdi (som kommer fra løsningen af vores funktion):
![]()
Hvis vi bruger denne værdi og tager det simple tilfælde, hvor a = 1, bliver vores funktion:
r(t) = e0.30635t
Vi vil bruge det fremragende gratis grafiske værktøj GeoGebra herfra.
Opsætning af den gyldne spiral ved hjælp af GeoGebra
Hvis vi nu graferer vores funktion på almindelige rektangulære koordinatakser i GeoGebra, får vi følgende eksponentialkurve. Bemærk, at r stiger med en stadig stigende hastighed (den bliver stejlere), når t stiger.
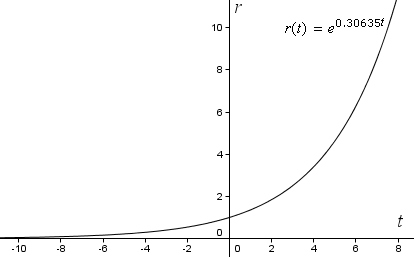
Men for at se en spiral skal vi grafte kurven ved hjælp af polære koordinater.
For at konvertere polarformen (som vi har fået) til rektangulær form (som vi har brug for til grafen) i Geogebra skal vi opstille og grafte følgende funktion:
a(t) = (r(t) cos(t), r(t) sin(t))
Lad os erstatte et par vigtige værdier for at se, hvad dette udtryk betyder. Hvis vi starter ved t = 0, får vi kurvens begyndelsespunkt:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Sådan betyder det, at vi starter 1 enhed fra oprindelsen langs den positive x-akse. Du kan se startpunktet i den følgende graf over spiralen.
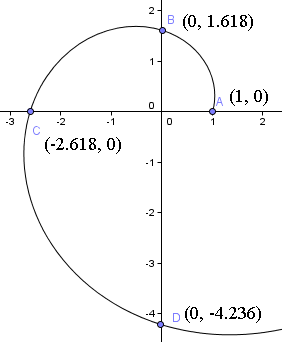
Næst roterer vi en kvart omgang og finder ved t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Bemærk, at vi nu befinder os 1,618 enheder fra oprindelsen op ad y-aksen. Det vil sige, at φ = 1,6180 gange den afstand, vi startede fra.
En anden rotation på en kvart omgang bringer os til t = π, hvor:
a(π) = (r(π) cos(π), r(π) sin(π)))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Vi er nu 2,618 enheder væk fra oprindelsen langs den negative x-akse, eller φ = 1,6180 gange den afstand fra oprindelsen, vi var ved den sidste kvart omdrejning.
Note:
φ2 = 2,6180
Vi kan beregne vores næste position, langs den negative y-akse, ved blot at gange denne sidste værdi med φ = 1,6180, hvilket giver os:
φ3 = 4,23606…
Så spiralen vil skære y-aksen ved (0, -4,236).
Et kvart omdrejning mere vil bringe os til φ4 = 6,85410… enheder langs den positive y-akse, dvs. (6,854, 0).
Vi kan se, at disse værdier er korrekte på vores spiralgraf ovenfor.
Hvis vi fortsætter, får vi en spiral som følger (det er 2 komplette omdrejninger, eller 4π = 720°):
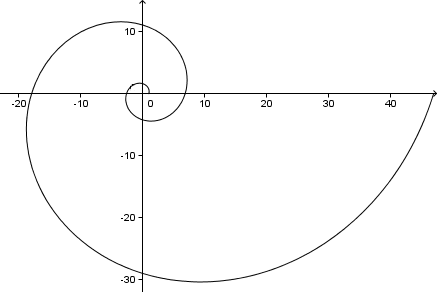
Som en sidebemærkning, da vi i denne opgave
cot b = 0.30635
så er
b = arccot 0,30635 = 1,274 radianer eller ca. 73°
Dette er den vinkel, som vores spiralarme danner med en linje fra spiralens centrum. Du kan se på grafen ovenfor, at hver spiralarm danner en vinkel på 73° med x-aksen (og y-aksen eller en hvilken som helst linje fra centrum).
Nærmer os den gyldne spiral ved hjælp af cirkelbuer
Vi kan opnå en spiral, der ligner den gyldne spiral meget ved at bruge cirkelbuer, der vokser i størrelse med det gyldne snit, på følgende måde.
Vi starter med et kvadrat på 1×1 og tegner en bue, centrum C, gennem 2 hjørner, således at siderne i kvadratet tangerer buen (dvs. de berører hinanden kun én gang).
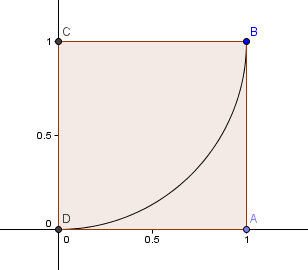
Dernæst placerer vi et kvadrat med sidelængden φ = 1.6180 over vores første kvadrat og konstruerer endnu en cirkelbue, centrum E, som før:
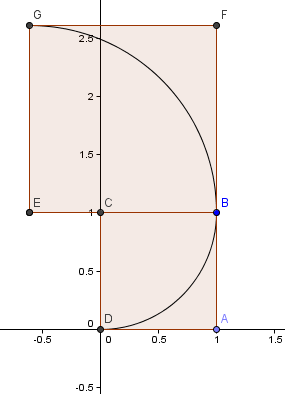
Vores næste kvadrat går til venstre og har sidelængden φ2 = 2,6180 = 1 + φ.
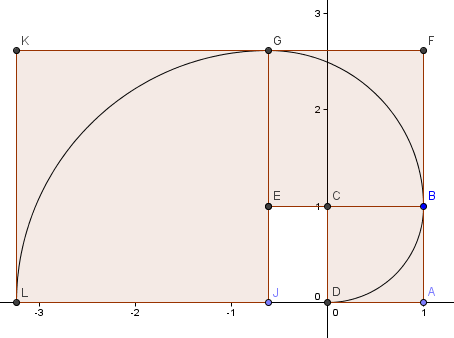
Vi fortsætter mønsteret (vi har gået endnu en hel omgang) og får en spiral, der ligner vores gyldne spiral fra før ganske meget.
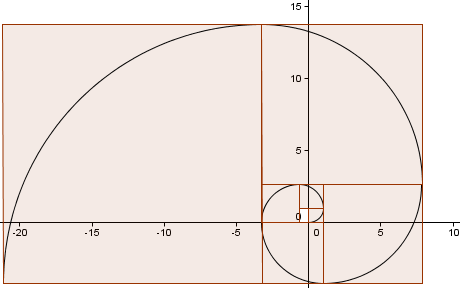
Hvor tæt er vores tilnærmelse?
Wikipedia’s artikel om den gyldne spiral har et billede, der hævder, at ovenstående spiral og den gyldne spiral er meget tæt på hinanden i form.
Her er det billede:
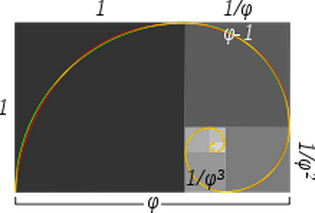
I billedteksten til billedet står der:
Nærliggende og ægte gyldne spiraler: Den grønne spiral er lavet af kvartcirkler, der tangerer det indre af hvert kvadrat, mens den røde spiral er en gylden spiral, en særlig type logaritmisk spiral. Overlappende dele vises gule. Længden af siden af et større kvadrat til det næste mindre kvadrat er i det gyldne snit.
Kan vi genskabe dette ?
På billedet nedenfor er den røde kurve den første del af den gyldne spiral, som vi konstruerede ovenfor, mens den grønne kurve er baseret på den tilnærmelse til en kvartdrejning, som vi lige har arbejdet med.
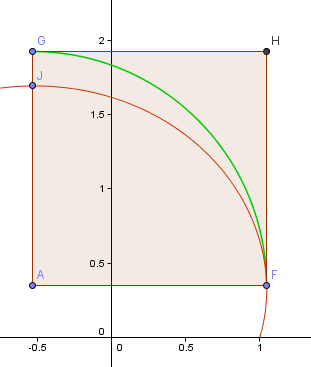
Punktet F er det “mest højre” punkt på spiralen, som vil være mit udgangspunkt for den kvartdrejede bue. Punktet J er det højeste punkt på denne del af spiralen.
Punkt A er skæringspunktet mellem de vandrette og lodrette linjer, der går gennem henholdsvis F og J, og dette vil være centrum for min bue.
Nu er buen GF slet ikke tæt på den relaterede del af spiralen FJ.
Lad os lave endnu et trin og se, om den næste del er bedre.
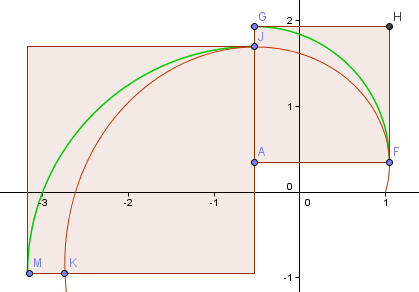
Som du kan se, er det værre (som forventet, da vi har bevæget os længere væk fra oprindelsen, og spiralarmen bliver større).
Det er klart, at dette aldrig kommer til at virke.
I min tidligere gyldne spiral brugte jeg imidlertid:
r(t) = e0,30635t
Konstanten a, havde værdien 1.
Hvis vi ønsker, at vores tilnærmede buer skal passe godt til den faktiske gyldne spiral, skal vi bruge en værdi på (nok ikke overraskende)
a = φ = 1,618103399..
Det giver os følgende kurver, svarende til grafen i Wikipedia.
Den røde kurve er den gyldne spiral,
r(t) = 1,618013 e0,30635t
Den grønne kurve er samlingen af cirkelbuer.
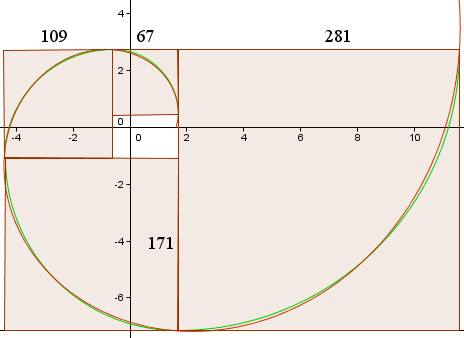
Firkanternes sidelængde (i pixels) er vist, og vi kan se, at de er omtrent i forholdet 1,618013…
Gylden spiral i medierne
Fra Wolfram’s Mathworld:
I sæson 4-afsnittet “Masterpiece” (2008) af CBS-tv-krimi-serien “Criminal Minds” konfronteres agenterne fra FBI’s adfærdsanalyseenhed med en seriemorder, der bruger Fibonacci-talrækken til at bestemme antallet af ofre for hver af sine drabsepisoder. I dette afsnit bemærker karakteren Dr. Reid også, at stederne for drabene ligger på grafen for en gylden spiral, og ved at gå til midten af spiralen kan Reid bestemme placeringen af morderens base.
Her er flere interessante oplysninger fra Wolfram’s Mathworld:
Logaritmisk spiral
For nørderne – design ved hjælp af den gyldne spiral
Der er mange, der mener, at design, der bruger det gyldne snit og den gyldne spiral, er en fryd for øjet.
Selv Twitter har for nylig omdesignet deres hovedside ved hjælp af den gyldne spiral.
Her er en god artikel af en fyr, der har konstrueret en gylden spiral uden billeder. (Mest for dem, der er interesseret i webdesign)
Gylden spiral uden billeder – ved hjælp af CSS og jQuery
Som han antyder i artiklen, er en elefants snabel også tæt på den gyldne spiral.

Elefantstamme – næsten en Golden Spiral
Konklusion
Den gyldne spiral er et interessant emne – et emne, der er værd at forfølge, ikke kun på grund af de behagelige designs, der er involveret, men også på grund af den interessante matematik bag dem.
Jeg håber, at det hjælper med at besvare dit spørgsmål, Pehr!