Die amortisierte Analyse wird für Algorithmen verwendet, die teure Operationen haben, die nur selten auftreten.

Die amortisierte Komplexitätsanalyse wird am häufigsten bei Datenstrukturen verwendet, die einen Zustand haben, der zwischen den Operationen bestehen bleibt.Der Grundgedanke ist, dass eine teure Operation den Zustand so verändern kann, dass der schlimmste Fall für lange Zeit nicht mehr eintreten kann, wodurch sich die Kosten amortisieren.
Lassen Sie T1, T2, …, Tk die Komplexität einer Folge von Operationen auf einer Datenstruktur sein. Die amortisierte Komplexität einer einzelnen Operation in dieser Folge ist (T1 + T2 + …+ Tk) / k.
Beispiel: ein dynamisches Array
In einem dynamischen Array werden Elemente am Anfang eines zugrundeliegenden festen Arrays gespeichert, und die verbleibenden Positionen sind unbenutzt.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Hier ist eine Ansicht des Speichers beim Anhängen der Elemente 2, 7, 1, 3, 8, 4 an ein anfänglich leeres Array mit der Kapazität 2.
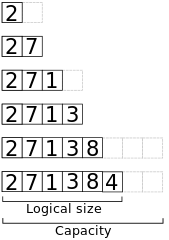
Worst-Case-Zeit
Die Worst-Case-Zeitkomplexität für das Anhängen eines Elements an ein Array der Länge n mit diesem Algorithmus ist Θ(n).Wenn das Array voll ist, weist der Algorithmus ein neues Array der Länge 2n zu und kopiert dann die Elemente aus dem alten Array in das neue.
Vorsichtlicherweise ist dieses Ergebnis zu pessimistisch.Die folgenden n Append-Operationen werden viel billiger sein – jede von ihnen wird in konstanter Zeit ablaufen, da das neu zugewiesene Array Platz für alle neuen Elemente hat.
Amortisierte Zeit
Eine Analyse der amortisierten Zeit gibt ein viel besseres Verständnis des Algorithmus.
Betrachten Sie eine Folge von n Append-Operationen, bei denen wir mit einem Array der Länge 1 beginnen. Eine sorgfältige Analyse zeigt, dass die Gesamtzeit dieser Operationen nur Θ(n) beträgt.
- Es gibt insgesamt n Zuweisungs- und Inkrementoperationen mit konstanter Zeit.
- Die Größenänderung erfolgt nur bei den Operationen 1, 2, 4, …, 2k, also insgesamt 1 + 2 + 4 + …+ 2k = 2-2k – 1 Elementkopieroperationen mit konstanter Zeit. Da 2k ≤ n ist, ist dies höchstens 2n – 1.
Daher ist die amortisierte Zeitkomplexität für eine einzelne Append-Operation Θ(1).
Mehr zur Algorithmusanalyse

Zeitkomplexität: Zähle deine Schritte

Big O Notation