Sun, 18 Jun 2006
1+1=2
Whitehead und Russells Principia Mathematica sind berühmt dafür, dass sie tausend Seiten brauchen, um zu beweisen, dass 1+1=2 ist. Natürlich beweist es auch eine Menge anderer Dinge. Hätten sie nur beweisen wollen, dass 1+1=2 ist, hätte es wahrscheinlich nur halb so viel Platz in Anspruch genommen.
Principia Mathematica ist ein merkwürdiges Buch, das es wert ist, sowohl aus historischer als auch aus mathematischer Sicht betrachtet zu werden. Es wurde um 1910 geschrieben, und die mathematische Logik steckte damals noch in den Kinderschuhen, frisch von der Transformation, die Peano und Frege an ihr vorgenommen hatten. Die Notation ist etwas undeutlich, denn die mathematische Notation hat sich seither erheblich weiterentwickelt. Wie ein schlecht geschriebenes Computerprogramm besteht ein großer Teil der Principia Mathematica aus wiederholtem Code, getrennten Abschnitten, die im Wesentlichen dasselbe sagen, weil die Autoren noch nicht die Techniken gelernt haben, die es erlauben würden, diese Abschnitte zu einem einzigen zusammenzufassen.
Zum Beispiel beginnt der Abschnitt ∗22, „Calculus of Classes“, mit der Definition der Teilmengenrelation (∗22.01), den Operationen der Mengenvereinigung und der Mengenschnittmenge (∗22.02 und .03), dem Komplement einer Menge (∗22.04) und der Differenz zweier Mengen (∗22.05). Anschließend werden die Kommutativität und Assoziativität von Mengenvereinigung und Mengenschnittmenge (∗22.51, .52, .57 und .7), verschiedene Eigenschaften wie !! (∗22.5) und dergleichen, bis hin zu Theoremen wie ∗22.92: !!\alpha\subset\beta \rightarrow \alpha\cup(\beta -\alpha)!!.
Der Abschnitt ∗23 ist „Calculus of Relations“ und beginnt fast genau so, indem er die Subrelation definiert (∗23.01), die Operationen der Vereinigung und der Überschneidung von Relationen (∗23.02 und .03), das Komplement einer Relation (∗23.04) und die Differenz zweier Relationen (∗23.05). Später beweist er die Kommutativität und Assoziativität der Vereinigung und der Schnittmenge von Relationen (∗23.51, .52, .57 und .7), verschiedene Eigenschaften wie !\alpha\dot\cap\alpha = \alpha! (∗22.5) und dergleichen, bis hin zu Theoremen wie ∗23.92: !!\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot-\alpha)!!.
Im Abschnitt ∗24 geht es um die Existenz von Mengen, die Nullmenge !!\Lambda!!, die Universalmenge !!{\rm V}!!, ihre Eigenschaften und so weiter, und dann wird Abschnitt ∗24 in ∗25 in einer Reihe von Theoremen über die Existenz von Relationen, die Null-Relation !!\dot\Lambda!!, die universelle Relation !!\dot {\rm V}!!, ihre Eigenschaften und so weiter verdoppelt.
So machten es Whitehead und Russell 1910. Wie würden wir es heute machen? Eine Relation zwischen S und T ist als Teilmenge von S × T definiert und ist somit eine Menge. Vereinigung, Schnittmenge, Differenz und die anderen Operationen sind für Relationen genau dieselben wie für Mengen, da Relationen Mengen sind. Alle Theoreme über Vereinigungen und Schnittmengen von Relationen, wie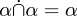 
, verschwinden einfach, weil wir sie bereits für Mengen bewiesen haben und Relationen Mengen sind. Die Nullrelation ist die Nullmenge. Die universelle Relation ist die universelle Menge.
Eine riesige Menge anderer Maschinerie verschwindet 2006, wegen der Vereinheitlichung von Relationen und Mengen. Principia Mathematica braucht eine spezielle Notation und eine spezielle Definition für das Ergebnis der Beschränkung einer Relation auf diejenigen Paare, deren erstes Element ein Mitglied einer bestimmten Menge S ist, oder deren zweites Element ein Mitglied von S ist, oder deren beide Elemente Mitglieder von S sind; 2006 würden wir einfach die gewöhnliche Mengenschnittoperation verwenden und von R ∩(S×B) oder was auch immer sprechen.
Whitehead und Russell konnten dies 1910 nicht tun, weil ein entscheidender Teil der Maschinerie fehlte: das geordnete Paar. Im Jahr 1910 wusste niemand, wie man ein geordnetes Paar nur aus Logik und Mengen aufbauen kann. Im Jahr 2006 (oder sogar 1956) würden wir das geordnete Paar <a, b> als die Menge {{a}, {a, b}} definieren. Dann würden wir als Theorem zeigen, dass <a, b> = <c, d> ist, wenn a=c und b=d ist, indem wir die Eigenschaften von Mengen verwenden. Dann würden wir A×B als die Menge aller p definieren, für die gilt: p = <a,b> ∧ a ∈ A ∧ b∈ B. Dann würden wir eine Beziehung zwischen den MengenA und B als Teilmenge von A×B definieren. Dann bekämen wir alle ∗23 und ∗25 und eine Menge ∗33 und ∗35 und ∗36 umsonst, und wahrscheinlich auch eine Menge anderer Dinge.
(Übrigens wurde die Sache mit {{a}, {a, b}} von Kuratowski erfunden. Normalerweise wird es Norbert Wiener zugeschrieben, aber Wieners Idee, obwohl ähnlich, war tatsächlich komplizierter.)
Es gibt keine geordneten Paare in Principia Mathematica, außer implizit. Es gibt auch kaum Mengen. Whitehead und Russell wollen alles auf die Logik gründen. Für Whitehead und Russell ist der grundlegende Begriff die „propositionale Funktion“, d.h. eine Funktion φ, deren Ausgang ein Wahrheitswert ist. Für jede solche Funktion gibt es eine entsprechende Menge, die sie mit !!\hat x\phi(x)!! bezeichnen, die Menge aller x, bei denen φ(x) wahr ist. Für Whitehead und Russell ist eine Relation durch eine Aussagefunktion zweier Variablen impliziert, analog zu der Art und Weise, wie eine Menge durch eine Aussagefunktion einer Variablen impliziert ist. Im Jahr 2006 verzichten wir auf „Funktionen von zwei Variablen“ und sprechen nur noch von Funktionen, deren (einziges) Argument ein geordnetes Paar ist; eine Relation wird dann zur Menge aller geordneten Paare, für die eine Funktion wahr ist.
Russell soll gesagt haben, dass die Entdeckung des Shefferstrichs (ein einziger logischer Operator, aus dem alle anderen logischen Operatoren aufgebaut werden können) ein enormer Fortschritt sei und alles verändern würde. Das erscheint uns heute seltsam, denn die Entdeckung des Sheffer-Strichs scheint so einfach zu sein, und sie ändert wirklich nichts Wichtiges. Man muss nur eine Notiz an den Anfang von Kapitel 1 anhängen, die besagt, dass ∼p und p∨q Abkürzungen für p|p bzw. p|p.|.q|q sind, die fünf grundlegenden Axiome beweisen und alles andere unverändert lassen. Aber Russell hätte mit einigem Recht dasselbe über die Entdeckung sagen können, dass geordnete Paare als Mengen interpretiert werden können, eine einfache Entdeckung, die die Principia Mathematica in der Tat in ein ganz anderes Werk verwandelt hätte.
Wie auch immer, mit diesem Hintergrund können wir den Beweis der Principia Mathematica für 1+1=2 diskutieren. Dies geschieht ziemlich am Ende der Principia Mathematica, im Abschnitt ∗102. Meine Kurzfassung geht nur bis ∗56, aber das reicht aus, um zu dem wichtigen Vorgängersatz ∗54.43 zu gelangen, der unten eingescannt ist:
Die Notation kann überwältigend sein, also konzentrieren wir uns nur auf die Aussage des Satzes und ignorieren alles andere, sogar die hilfreiche Anmerkung am Ende:
Dies ist der Satz, der bewiesen wird; was folgt, ist der Beweis.
Nun sollte ich die Notation erklären, die sich seit 1910 etwas verändert hat. Zunächst einmal wird in Principia Mathematica die Peano’sche Punktnotation verwendet, um den Vorrang zu disambiguieren, während wir jetzt Klammern verwenden. Die Punktschreibweise ist etwas gewöhnungsbedürftig, hat aber einige deutliche Vorteile gegenüber der Klammerschreibweise. Die Idee ist einfach, dass man die Gruppierung durch das Einfügen von Punkten anzeigt, so dass (1+2)×(3+4)&mal(5+6) als1+2.×.3+4.×.5+6 geschrieben wird. Die mittlere Teilformel steht zwischen mehreren Punkten. Die Teilformel (1+2) steht ebenfalls zwischen zwei Punkten, aber der Punkt am linken Ende ist überflüssig und wird weggelassen; ebenso wird die Teilformel (5+6) durch einen Punkt auf der linken Seite und durch das Ende der Formel auf der rechten Seite abgegrenzt.
Was, wenn man Klammern verschachteln muss? Dann verwendet man weitere Punkte. Ein doppelter Punkt (:) ist wie ein einzelner Punkt, aber stärker. Zum Beispiel schreiben wir ((1+2)×3)+4 als 1+2 . × 3 : + 4, und der doppelte Punkt isoliert den gesamten Ausdruck 1+2 . × 3 in eine einzelne Teilformel, für die +4 gilt.
Manchmal braucht man mehr Rangstufen, dann verwendet man Dreifachpunkte (.: und :.) und Vierfachpunkte (::). Diese Formel hat, wie Sie sehen, doppelte und dreifache Punkte. Übersetzt man die Punkte in die Standardparenthesenschreibweise, so ergibt sich $$$54.43. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$. Dies sieht etwas unübersichtlicher aus als die Version mit den Punkten, und bei komplizierten Formeln kann man Schwierigkeiten haben, herauszufinden, welche Klammern zu welchen passen. Mit den Punkten ist es immer einfach. Daher finde ich es etwas schade, dass diese Konvention nicht mehr verwendet wird.
Das Symbol !!\vdash!! hat sich nicht geändert; es bedeutet, dass die Formel, auf die es angewendet wird, als wahr behauptet wird. !!\supset!! ist die logische Implikation und !!\equiv!! die logische Äquivalenz. Λ ist die leere Menge, die wir heute als ∅ schreiben. ∩ ∪ und ∈ haben ihre modernen Bedeutungen: ∩ und ∪ sind die Mengenschnittmenge und der Vereinigungsoperator, und x∈y bedeutet, dass x ein Element der Menge y ist.
Die übrigen Punkte sind semantisch. α und β sind Mengen. 1bezeichnet die Menge aller Mengen, die genau ein Element haben. Das heißt, es ist die Menge { c : es existiert a so, dass c = {a } }. Theoreme über 1 sind zum Beispiel:
- dass Λ∉1 (∗52.21),
- dass wenn α∈1 dann gibt es irgendein x so dass α ={x} (∗52.1), und
- dass {x}∈1 (∗52.22).
2 ist ebenfalls die Menge aller Mengen, die genau zwei Elemente haben. Ein wichtiger Satz über 2 ist ∗54.3, der besagt, dass $$\ast54.3. \vdash 2 = \hat\alpha\{ (\existiert x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\in 1 \}.$$In der Notation der Principia Mathematica wird {x}, die Menge, die x und nichts anderes enthält, ι’x geschrieben, so dass dieser Satz besagt, dass 2 identisch ist mit der Menge aller α, so dassα ein Element x hat, das, wenn es aus α entfernt wird, eine Menge mit 1 Element übrig lässt.
Hier ist also wieder der Satz ∗54.43:
Er besagt, dass, wenn die Mengen α und β jeweils genau ein Element haben, sie nur dann disjunkt sind (d.h. keine gemeinsamen Elemente haben), wenn ihre Vereinigung genau zwei Elemente hat.
Der Beweis, der im obigen Scan nach dem Wort „Dem.“ (kurz für „Demonstration“) erscheint, geht so:
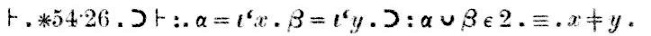
„Theorem ∗54.26implies that if α = {x} and β = {y}, thenα∪β has 2 elements if and only if x isdifferent from y.“
„Nach Satz ∗51.231 ist dieser letzte Teil (x ist verschieden vony) wahr, wenn und nur wenn {x} und {y} disjunkt sind.“
„Nach ∗13.12 ist dieses letzte Bit ({x} und {y} sind disjunkt) wahr, wenn und nur wenn α und β selbst disjunkt sind.“ Der Teilschluss an dieser Stelle, der mit (1) bezeichnet ist, lautet: Wenn α = {x} und β ={y}, dann ist α∪β ∈ 2, wenn und nur wennα∩β = Λ.
Der Beweis geht weiter: „Schlussfolgerung (1), mit den Theoremen ∗11.11 und ∗11.35, impliziert, dass, wenn es x und y gibt, so dass α{x} und β {y} ist, dann α∪β ∈ 2wenn und nur wenn α und β disjunkt sind.“ Diese Schlussfolgerung wird mit (2) bezeichnet.
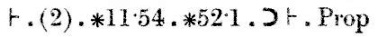
Schließlich impliziert die Schlussfolgerung (2) zusammen mit den Theoremen ∗11.54 und ∗52.1 das Theorem, das wir zu beweisen versuchten.
Vielleicht fällt hier auf, wie klein die Schritte sind.∗54.26, von dem dieses Theorem stark abhängt, ist fast dasselbe; es besagt, dass {x}∪{y} ∈ 2 dann und nur dann, wenn x≠y. ∗54.26 hängt wiederum von ∗54.101 ab, das besagt, dass α nur dann 2 Elemente hat, wenn es x und y gibt, die nicht gleich sind, so dass α = {x} ∪{y}. ∗54.101 unterscheidet sich nur geringfügig von der Definition von 2. Der Satz ∗51.231 besagt, dass {x} und {y} dann und nur dann disjunkt sind, wenn x und y verschieden sind.∗52.1 ist eine grundlegende Eigenschaft von 1; wir haben sie bereits gesehen.
Die anderen in der Demonstration zitierten Sätze sind sehr kleine technische Angelegenheiten. ∗11.54 besagt, dass man eine Behauptung, dass zwei Dinge existieren, in zwei Behauptungen aufteilen kann, von denen jede behauptet, dass eines der Dinge existiert. ∗11.11 ist noch schlanker: Es besagt, dass, wenn φ(x, y) immer wahr ist, man einen universellen Quantor anhängen und behaupten kann, dass φ(x, y) für alle x und y wahr ist. ∗13.12 betrifft die Ersetzung von Gleichen durch Gleiche: Wenn x und y gleich sind, dann besitzt x eine Eigenschaft ψ nur dann, wenn y auch eine hat.
Ich habe die späteren Teile der Principia Mathematica nicht gesehen, weil mein Exemplar nach dem Abschnitt ∗56 aufhört, und die arithmetischen Sachen sind viel später. Aber dieses Theorem hat eindeutig den Sinn von 1+1=2 in sich, und das spätere Theorem (∗110.643), das tatsächlich 1+1=2 behauptet, hängt stark von diesem ab.
Auch wenn ich mir nicht ganz sicher bin, was später passieren wird (ich habe schon viel zu viel Zeit damit verschwendet, um noch mehr Zeit zu investieren, um die Vollversion aus der Bibliothek zu holen), kann ich eine fundierte Vermutung anstellen. Principia Mathematica wird die Zahl 17 als die Menge aller 17-elementigen Mengen definieren und in ähnlicher Weise jede andere Zahl; die Verwendung des Symbols 2 zur Darstellung der Menge aller 2-elementigen Mengen deutet dies an. Diese Mengen aller Mengen einer bestimmten Größe werden dann als „Kardinalzahlen“ bezeichnet.
In den Principia Mathematica wird die Summe der Kardinalzahlen p und q etwa so definiert: Man nehme eine repräsentative Menge a von p; a hat p Elemente. Nimm eine repräsentative Menge b von q; b hat q Elemente. Es sei c =a∪b. Wenn c zu einer Kardinalzahl r gehört und a und b disjunkt sind, dann ist die Summe von p und q r.
Mit dieser Definition kann man die üblichen wünschenswerten Eigenschaften der Addition beweisen, wie x + 0 = x, x + y = y + x und 1 + 1 = 2.
Insbesondere folgt 1+1=2 direkt aus Satz ∗54.43; das ist genau das, was wir wollen, denn um 1+1 zu berechnen, müssen wir zwei disjunkte Repräsentanten von 1 finden und ihre Vereinigung nehmen; ∗54.43 behauptet, dass die Vereinigung ein Element von 2 sein muss, unabhängig davon, welche Repräsentanten wir wählen, so dass 1+1=2.
Post scriptum: Peter Norvig sagt, dass der Zirkumflex in der Principia Mathematica Notation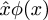 
die eigentliche Quelle für die Verwendung des Wortes Lambda ist, um eine anonyme Funktion in den Programmiersprachen Lisp und Python zu bezeichnen. Sie wissen sicher, dass diese Sprachen „lambda“ von der Verwendung des griechischen Buchstabens λ durch Alonzo Church zur Darstellung der Funktionsabstraktion in seinem „λ-Kalkül“ erhalten haben: In Lisp ist (lambda (u) B) eine Funktion, die ein Argumentu annimmt und den Wert von B zurückgibt; im λ-Kalkül ist λu.B eine Funktion, die ein Argumentu annimmt und den Wert von B zurückgibt. Norvig sagt, dass Church ursprünglich plante, die Funktionλu.B als û.B zu schreiben, aber sein Drucker konnte keine Zirkumflex-Akzente setzen. Also erwog er, den Zirkumflex nach links zu verschieben und stattdessen ein großes Lambda zu verwenden:Λu.B. Das große Λ sah zu sehr nach logisch und ∧ aus, was verwirrend war, also benutzte er stattdessen ein kleines Lambdaλ.
Post post scriptum: Alle sagen immer „Russell und Whitehead“.Google-Ergebnisse für „Russell und Whitehead“ übertreffen die für „Whitehead und Russell“ zum Beispiel um das Doppelte. Und warum? Auf dem Umschlag und auf der Titelseite steht „Alfred North Whitehead und Bertrand Russell, F.R.S.“. Wie und wann hat Whitehead den ersten Platz auf der Titelseite verloren?
Permanenter Link