- Text
- Probleme
- Zielerreichung
- Fill in the Blanks
- Multiple Choice
- Glossar
Die theoretisch vorzuziehende Methode zur Erfassung der Abschreibung ist die Effektivzinsmethode. Der Zinsaufwand ist ein konstanter Prozentsatz des Buchwerts der Anleihe und nicht jedes Jahr ein gleicher Dollarbetrag. Der theoretische Vorteil besteht darin, dass die Zinsberechnung mit der Grundlage übereinstimmt, auf der die Anleihe bewertet wurde.
Der Zinsaufwand wird als Effektivzinssatz mal dem Buchwert der Anleihe für jede Periode berechnet. Die Höhe der Amortisation ist die Differenz zwischen den gezahlten Zinsen und dem berechneten Zinsaufwand für die Anleihe.
Prämienbeispiel
Erinnern Sie sich daran, dass Schultz bei der Ausgabe seiner Anleihen mit einer Rendite von 6 % 108.530 $ erhalten hat. Die effektiven Zinsen für die ersten sechs Monate betragen also 108.530 $ X 6% X 6/12 = 3.255,90 $. Von diesem Betrag werden 4.000 $ in bar gezahlt und 744,10 $ (4.000 $ – 3.255,90 $) sind Prämienabschreibungen. Die Tilgung des Agios verringert den Nettobuchwert der Schuld auf 107.785,90 $ (108.530 $ – 744,10 $). Dieser neue Saldo würde dann zur Berechnung der Effektivzinsen für die nächste Periode verwendet werden. Dieser Vorgang würde sich in jeder Periode wiederholen, wie in der folgenden Tabelle dargestellt:
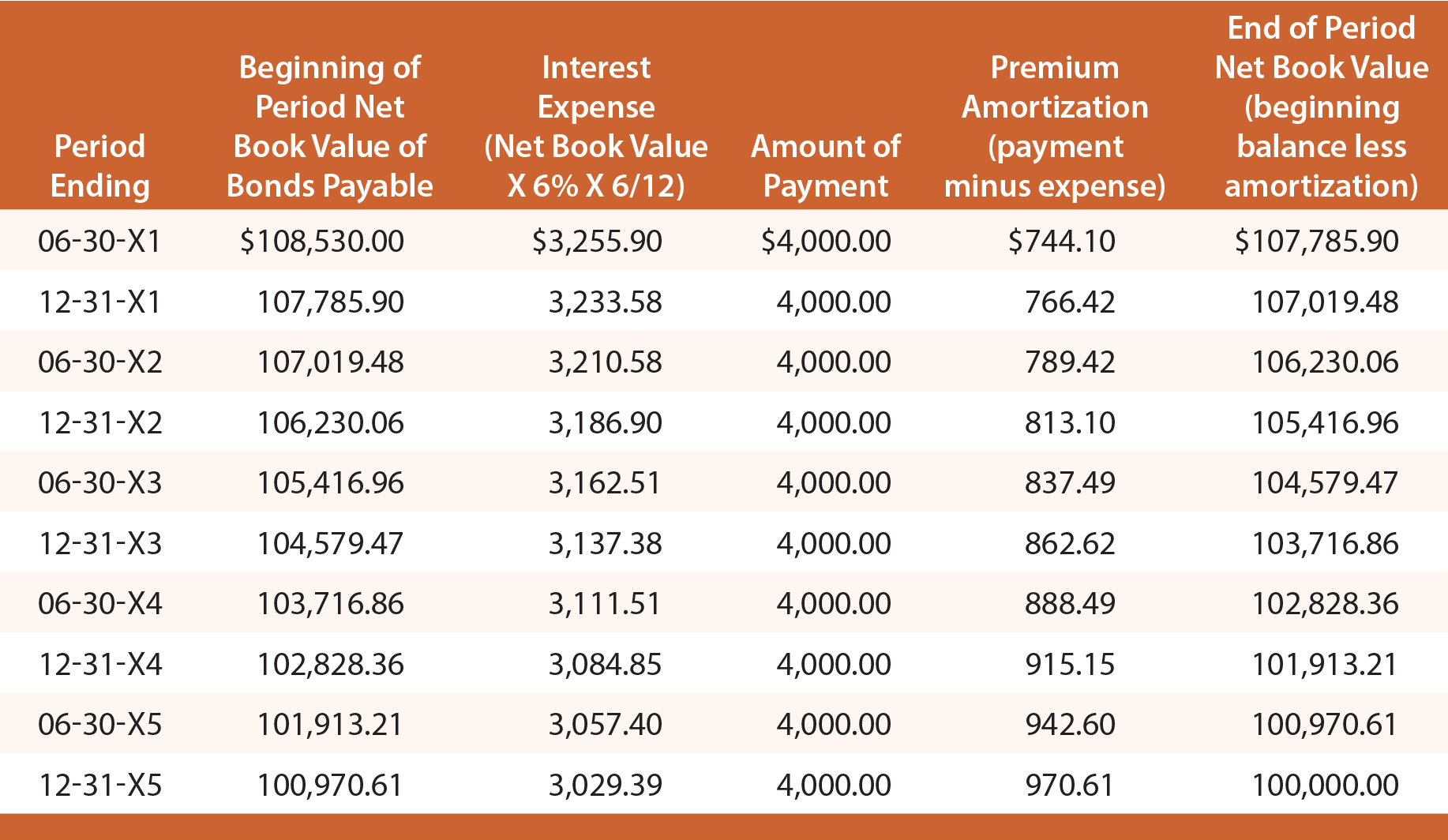
Die anfängliche Journalbuchung zur Erfassung der Ausgabe der Anleihen und die abschließende Journalbuchung zur Erfassung der Rückzahlung bei Fälligkeit wären identisch mit denen, die für die lineare Methode gezeigt werden. Die einzelnen Journalbuchungen zur Erfassung des periodischen Zinsaufwands würden jedoch variieren und können anhand der vorstehenden Tilgungstabelle ermittelt werden.
Die folgende Buchung würde die Zinsen am 30. Juni 20X3 erfassen:

Der folgende Bilanzausweis wäre zum 30. Juni 20X3 angemessen:

Abzinsungsbeispiel
Erinnern Sie sich daran, dass Schultz bei der Ausgabe seiner Anleihen mit einer Rendite von 10 % nur 92.278 $ erhalten hat. Die effektiven Zinsen für die ersten sechs Monate betragen also 92.278 $ X 10% X 6/12 = 4.613,90 $. Von diesem Betrag werden 4.000 $ in bar gezahlt, und 613,90 $ sind Diskontabschreibungen. Durch die Diskontamortisation erhöht sich der Nettobuchwert der Schuld auf 92.891,90 $ (92.278,00 $ + 613,90 $). Dieser neue Saldo würde dann zur Berechnung der Effektivzinsen für die nächste Periode verwendet werden. Dieser Vorgang würde sich in jeder Periode wie folgt wiederholen:
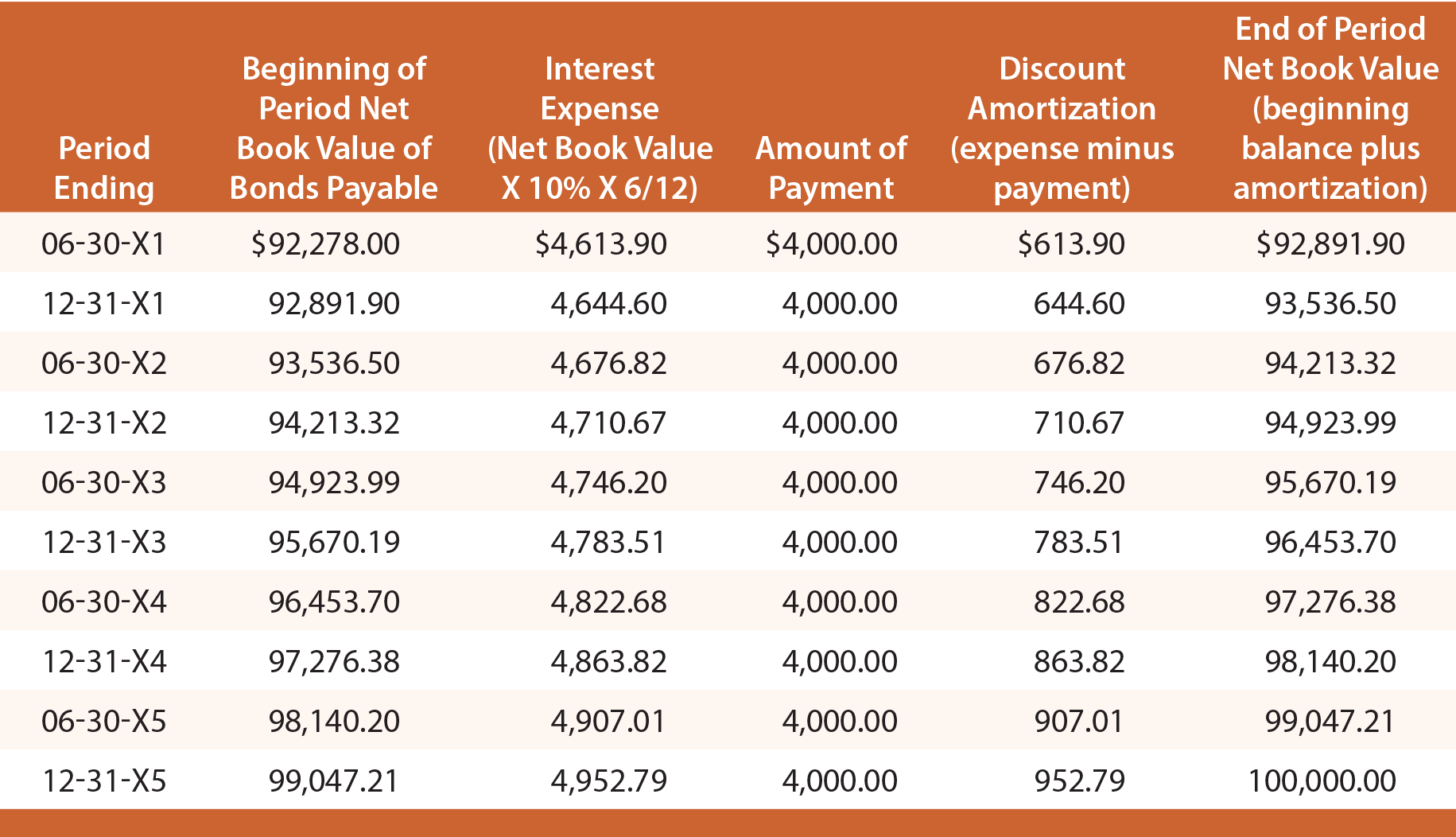
Jeder Journaleintrag zur Verbuchung des periodischen Zinsaufwands würde variieren und kann durch Bezugnahme auf die vorangehende Amortisationstabelle bestimmt werden. Zum Beispiel würde die folgende Buchung die Zinsen am 30. Juni 20X3 erfassen und zu dem unten stehenden Bilanzausweis führen: