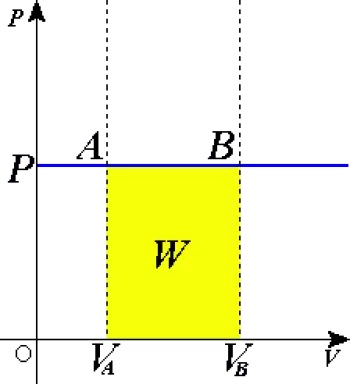
Ein isobarer Prozess ist ein thermodynamischer Prozess, bei dem sich der Zustand einer bestimmten Stoffmenge ändert, wobei der Druck konstant bleibt. Was er ändern kann, ist eine oder mehrere seiner Zustandsgrößen. Wird dem System Wärme zugeführt, wird Arbeit verrichtet und die innere Energie des Systems ändert sich ebenfalls.
In einem Druck-Volumen-Diagramm treibt er nach dem idealen Gasgesetz eine horizontale Linie an.
Der isobare Prozess wird durch das Charles’sche Gesetz geregelt. Nach dem Charles’schen Gesetz ist für eine feste Masse eines idealen Gases bei konstantem Druck das Volumen direkt proportional zur Kelvin-Temperatur.
Isobare Prozesse werden durch den ersten Hauptsatz der Thermodynamik geregelt. Bei diesen Prozessen ist die Energiezunahme gleich der Enthalpiezunahme minus dem Druck multipliziert mit der Volumenzunahme:ΔE = ΔH – P – ΔV.
Nicht zu verwechseln mit isothermen Prozessen, die bei konstantem Druck ablaufen oder mit adiabatischen Prozessen, bei denen kein Wärmeaustausch stattfindet. Bei diesen Prozessen kann eine Druckänderung auftreten. Wenn der Prozess in einem konstanten Volumen abläuft, spricht man von einem isochoren Prozess.
Isobare Prozessbeispiele
Um diesen thermodynamischen Prozess besser zu verstehen, helfen uns ein paar Beispiele.
-
Expansionsphase des Zylinders eines Motors.
-
Wasser in einem offenen Behälter kochen.
-
Erwärmung eines Globus durch Sonneneinstrahlung.
-
Heißluftballons experimentieren mit isobaren und isochronen Prozessen.
Erwärmung der Luft eines Ballons
Zu Beginn des Morgens weist er einen bestimmten Druck, ein bestimmtes Volumen und eine bestimmte Temperatur auf; wenn sich die Luft im Inneren erwärmt, erhöht sich der Druck, der jedoch aufgrund der Zunahme des Volumens nicht variiert.
Zylinderexpansionsphase einer Wärmekraftmaschine
Der Zylinder einer Wärmekraftmaschine kann je nach Phase des Zyklus expandiert oder kontrahiert werden. Die Expansion der Luft in einem Zylinder mit einem beweglichen Kolben, dem Wärme zugeführt wird, erfolgt durch einen isobaren Prozess. In gleicher Weise wird bei der Kompression das Volumen isobar reduziert.
Das Volumen nimmt proportional zur Temperatur zu und der Druck bleibt konstant. Dies entspricht dem Charles’schen Gesetz.
Wasserkochen in einem offenen Gefäß
Ein alltägliches Beispiel für einen isobaren Vorgang ist das Kochen von Wasser in einem offenen Gefäß. Wenn man dem Wasser Wärmeenergie zuführt, steigt seine Temperatur und es wird zu Dampf.
Der entstandene Dampf hat eine höhere Temperatur und nimmt ein größeres Volumen ein, der Druck bleibt jedoch konstant. Der Druck ist von Anfang an gleich dem atmosphärischen Druck.
Erwärmung eines Heißluftballons
Ein Heißluftballon ist ein Beispiel für den isobaren Prozess.
Heißluftballons funktionieren, weil heiße Luft aufsteigt. Indem man die Luft im Inneren des Ballons mit dem Brenner erhitzt, wird sie leichter als die kühlere Luft an der Außenseite. Dadurch schwebt der Ballon nach oben, als befände er sich im Wasser.
Der Druck im Inneren des Ballons ist der gleiche wie der atmosphärische. Wenn der Pilot Wärme in die Luft einleitet, steigt die Temperatur. Dadurch verringert sich die Dichte der Luft, und aufgrund des Unterschieds zwischen ihrer Dichte und der der Luft steigt der Ballon auf.
Thermodynamisch gesehen wird ein Teil der Wärme in Arbeit umgewandelt, wodurch der Heißluftballon aufsteigt. Ein Teil dieser Wärme wird wegen des thermodynamischen Kontakts mit der Außenluft und wegen des Verlusts der heißen Luft beim Ausdehnen außerhalb des Systems abgegeben.
W 1-2 = P ( V 2 – V 1 ) W 1-2 = n R ( T 2 – T 1 ) Q 1-2 = m c p ( T 2 – T 1 ) Q 1-2 = ( k / ( k -1)) P ( V 2 – V 1 )
Wobei,
-
W 1-2 die durch die Zustandsänderung geleistete Arbeit
-
Q 1-2 die zugeführte oder abgeführte Wärmemenge
-
P der Druck
-
V das Volumen
-
T die absolute Temperatur
-
n die Staubmenge (gewöhnlich in Molen ausgedrückt)
-
m die Masse des Stoffes
-
cp die spezifische Wärme des Stoffes bei konstantem Druck
-
k ist ein Verhältnis, das dem Quotienten aus der spezifischen Wärme bei konstantem Druck und konstantem Volumen entspricht,
Aus der ersten Gleichung geht hervor, dass das System positive Arbeit leistet, wenn es sich ausdehnt (ΔV ist positiv). Im Gegenteil, wenn die Volumenzunahme negativ ist, zieht sich das System zusammen und die Arbeit ist negativ.
Zustandsgleichung eines idealen Gases
Die Zustandsgleichung eines idealen Gases (manchmal auch die Mendelejew-Clapeyron-Gleichung oder die Clapeyron-Gleichung) ist eine Formel, die die Beziehung zwischen Druck, molarem Volumen und absoluter Temperatur eines idealen Gases herstellt. Die Gleichung lautet:
pV = nRT
Wobei,
p – Druck,
V- Gasvolumen,
n- die Gasmenge,
R – universelle Gaskonstante, R ≈ 8.314 J / (mol⋅K),
T – thermodynamische Temperatur, K Kelvin.