- Lernziele
- Netze
- Beispiel 1
- Beispiel 2
- Übungsaufgaben
- Antworten
- Prismen
- Flächeninhalt eines Prismas mit Hilfe von Netzen
- Beispiel 3
- Übungsaufgaben
- Antworten
- Zylinder
- Flächeninhalt eines Zylinders mit Hilfe von Netzen
- Beispiel 4
- Oberfläche eines Zylinders mit Hilfe einer Formel
- Beispiel 5
- Beispiel 6
- Beispiel 7
- Kugeln
- Flächeninhalt einer Kugel
- Beispiel 8
- Beispiel 9
- Übungsaufgaben
- Antworten
Lernziele
- Netze verstehen.
- Netze zur Darstellung von Prismen verwenden.
- Bestimme den Flächeninhalt eines Prismas.
- Bestimme den Flächeninhalt von Zylindern.
- Bestimme den Flächeninhalt einer Kugel.
Netze
Eine letzte Möglichkeit, einen Körper darzustellen, ist die Verwendung eines Netzes. Wenn du ein Netz ausschneidest, kannst du es zu einem Modell einer Figur falten. Netze können auch verwendet werden, um einen einzelnen Körper zu analysieren. Hier ist ein Beispiel für ein Netz für einen Würfel.
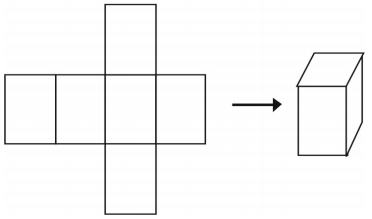
Es gibt mehr als eine Möglichkeit, ein Netz für eine einzelne Figur zu machen.
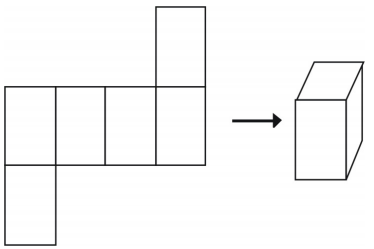
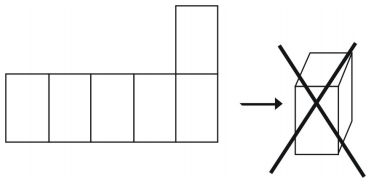
Allerdings ergeben nicht alle Anordnungen einen Würfel.
Beispiel 1
Welche Art von Figur erzeugt das Netz? Zeichne die Figur.
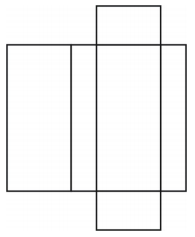
Das Netz erzeugt ein kastenförmiges rechteckiges Prisma wie unten gezeigt.
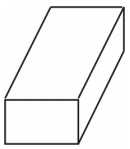
Beispiel 2
Welches Netz kannst du zeichnen, um die gezeigte Figur darzustellen? Zeichne das Netz.
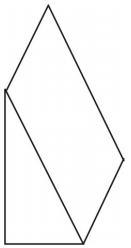
Ein Netz für das Prisma ist dargestellt. Andere Netze sind möglich.
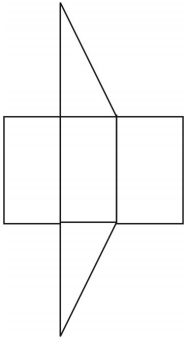
Übungsaufgaben
Zeichne zu jedem der folgenden Punkte ein Netz:
Antworten
Prismen
Ein Prisma ist eine dreidimensionale Figur mit einem Paar paralleler und kongruenter Enden oder Basen. Die Seiten eines Prismas sind Parallelogramme. Prismen werden durch ihre Basen gekennzeichnet.
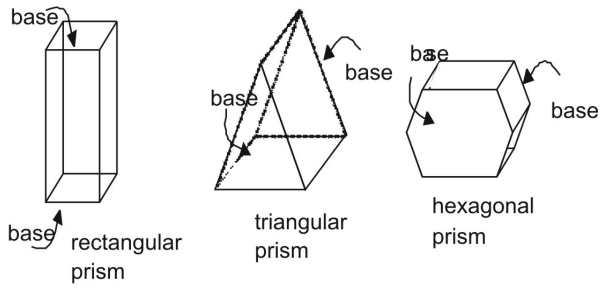
Flächeninhalt eines Prismas mit Hilfe von Netzen
Die obigen Prismen sind rechte Prismen. Bei einem rechten Prisma stehen die Seitenflächen senkrecht zu den Grundflächen des Prismas. Vergleiche ein rechtes Prisma mit einem schiefen Prisma, bei dem Seiten und Grundflächen nicht senkrecht sind.
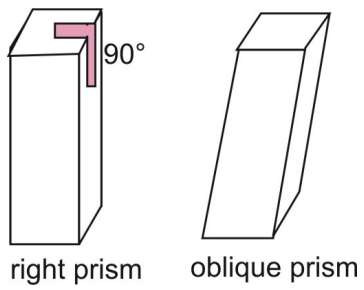
Zwei Postulate, die für den Flächeninhalt gelten, sind das Flächenkongruenzpostulat und das Flächenadditionspostulat.
Mit Hilfe eines Netzes und des Flächenadditionspostulats kann man den Flächeninhalt eines rechten Prismas bestimmen.
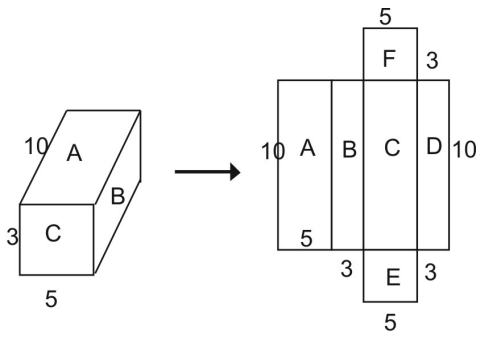
Aus dem Netz kann man ersehen, dass der Flächeninhalt des gesamten Prismas gleich der Summe der Figuren ist, aus denen das Netz besteht:
Gesamter Flächeninhalt = Fläche A + Fläche B + Fläche C + Fläche D + Fläche E + Fläche F
Anhand der Formel für den Flächeninhalt eines Rechtecks kann man sehen, dass der Flächeninhalt des Rechtecks A ist:
A = l – w
A = 10 – 5 = 50 Quadrateinheiten
Auch die Flächen der anderen Rechtecke werden wieder in die obige Gleichung eingesetzt.
Gesamtoberfläche = Fläche A + Fläche B + Fläche C + Fläche D + Fläche E + Fläche F
Gesamtoberfläche = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3)
Gesamtoberfläche = 50 + 30 + 50 + 30 + 15 + 15
Gesamtoberfläche = 190 Quadrateinheiten
Beispiel 3
Benutze ein Netz, um die Oberfläche des Prismas zu bestimmen.
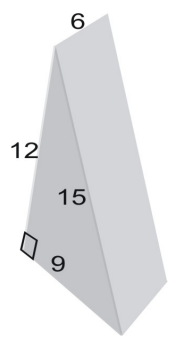
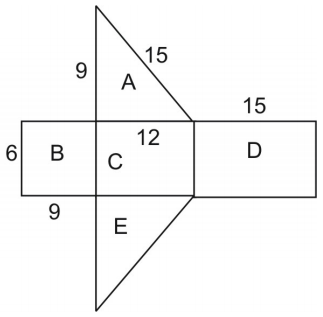
Der Flächeninhalt des Netzes ist gleich dem Flächeninhalt der Figur. Um den Flächeninhalt des Dreiecks zu bestimmen, verwenden wir die Formel:
\displaystyle{A}=\frac{1}{2}hb\, wobei h die Höhe des Dreiecks und b seine Basis ist.
Beachte, dass die Dreiecke A und E kongruent sind, so dass wir den Flächeninhalt von Dreieck A mit 2 multiplizieren können.
\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\\
\displaystyle\text{}=2(\text{area }A)+\text{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, beträgt die Oberfläche 324 Quadrateinheiten.
Übungsaufgaben
Bestimme für jede der folgenden Aufgaben den Flächeninhalt a mit Hilfe der Netzmethode und den Umfang


- Die Grundfläche eines Prismas ist ein rechtwinkliges Dreieck, dessen Schenkel 3 und 4 sind und dessen Höhe 20 beträgt. Wie groß ist die Gesamtfläche des Prismas?
- Ein rechtwinkliges sechseckiges Prisma ist 24 Zoll hoch und hat Basen, die regelmäßige Sechsecke sind, die 8 Zoll auf einer Seite messen. Wie groß ist die Gesamtoberfläche?
- Wie groß ist das Volumen des Prismas in Aufgabe 4?
In den folgenden Fragen ist eine Scheune wie ein fünfeckiges Prisma geformt, dessen Abmessungen in Fuß angegeben sind:

- Wie viele Quadratfuß (ohne das Dach) hat die Oberfläche der zu streichenden Scheune?
- Wenn eine Gallone Farbe 250 Quadratmeter abdeckt, wie viele Gallonen Farbe werden dann für den Anstrich der Scheune benötigt?
- Ein Karton ist ein perfekter Würfel mit einer Kante von 17 Zoll. Wie viele Kubikmeter kann er fassen?
- Ein Schwimmbad ist 16 Fuß breit, 32 Fuß lang und gleichmäßig 4 Fuß tief. Wie viele Kubikmeter Wasser kann er fassen?
- Eine Müslischachtel ist 25 cm lang, 9 cm breit und 30 cm hoch. Wie viel Müsli kann sie fassen?
Antworten
Netze und Umfang:
- 40.5 in2
- 838 cm2
- 252 Quadrateinheiten
- 1484.6 Quadrateinheiten
- 3990.7 cubic inches
Die Scheune:
- 2450 square feet
- 10 gallons of paint
- 2.85 cubic feet (Vorsicht hier. Die Einheiten in der Aufgabe sind in Zoll angegeben, aber die Frage fragt nach Fuß.)
- 2048 Kubikfuß
- 6750 cm3
Zylinder
Ein Zylinder ist eine dreidimensionale Figur mit einem Paar paralleler und kongruenter kreisförmiger Enden oder Basen. Ein Zylinder hat eine einzige gekrümmte Seite, die in der Ebene ein Rechteck bildet.
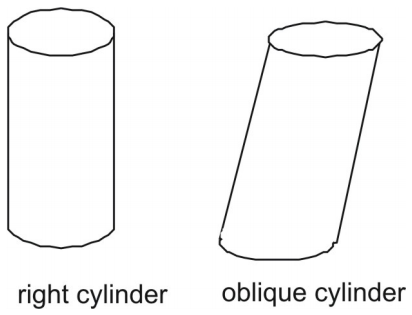
Wie bei Prismen können Zylinder rechtwinklig oder schräg sein. Die Seite eines rechten Zylinders steht senkrecht zu seiner kreisförmigen Grundfläche. Die Seite eines schrägen Zylinders steht nicht senkrecht zu seinen Grundflächen.
Flächeninhalt eines Zylinders mit Hilfe von Netzen
Sie können einen Zylinder in ein Netz zerlegen.
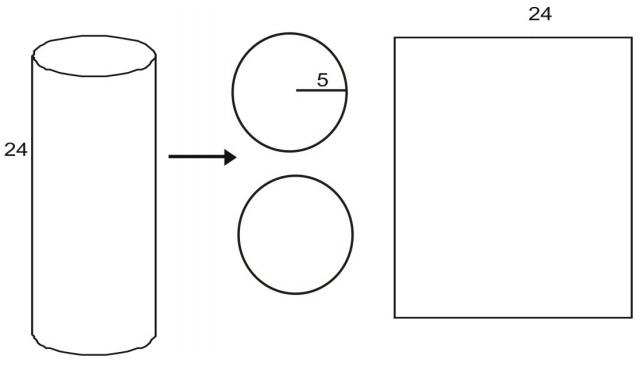
Der Flächeninhalt jeder Grundfläche ist gegeben durch den Flächeninhalt eines Kreises:
A=\pi{r}^2\\
A=\pi(5)^2\\
A=25\pi\
A\approx(25)(3.14)=78.5\\
Der Flächeninhalt der rechteckigen Seitenfläche L ist gegeben durch das Produkt aus Breite und Höhe. Die Höhe ist mit 24 angegeben. Man sieht, dass die Breite der Fläche gleich dem Umfang der kreisförmigen Grundfläche ist.
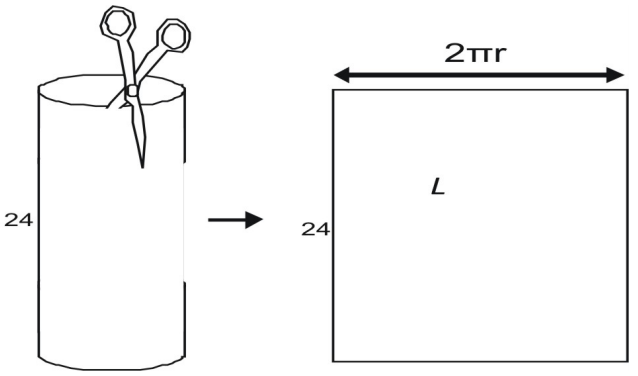
Um die Breite zu ermitteln, stelle man sich vor, dass man einen dosenartigen Zylinder mit einer Schere zerschneidet. Wenn du die Seitenfläche abschneidest, siehst du, dass sie gleich dem Umfang des Dosenoberteils ist. Der Umfang eines Kreises ist gegeben durch C = 2πr, die Seitenfläche, L, ist
L=2{\pi}rh\\
L=2{\pi}(5)(24)\\
L=240\pi\
L\approx(240)(3.14)=753,6\\
Nun können wir die Fläche des gesamten Zylinders mit A = (Fläche der beiden Grundflächen) + (Fläche der Seitenfläche) ermitteln.
A=2(75,36)+753,6\\
A=904,32\\
Sie sehen, dass die Formel, die wir verwendet haben, um die Gesamtoberfläche zu finden, für jeden rechten Zylinder verwendet werden kann.
Beispiel 4
Bestimme den Flächeninhalt des Zylinders mit einem Netz.
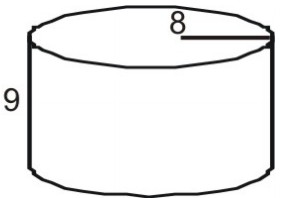
Zunächst zeichne und beschrifte ein Netz für die Figur.
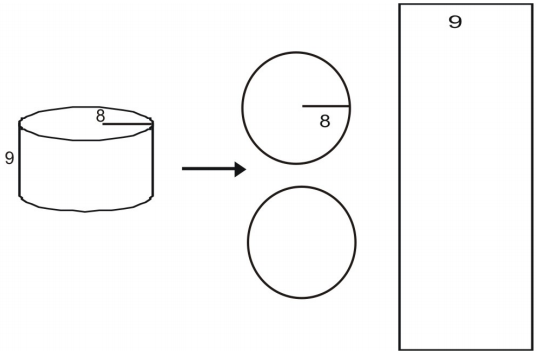
Berechne den Flächeninhalt jeder Grundfläche.
A=\pi{r}^2\\
A=\pi(8)^2\
A=64\pi\
A\ca.(64)(3.14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\\
Bestimme die Fläche des gesamten Zylinders.
A=2(200.96)+452.16\
A=854.08\\
Die Gesamtoberfläche beträgt also ungefähr 854,08 Quadrateinheiten
Oberfläche eines Zylinders mit Hilfe einer Formel
Sie haben gesehen, wie man Netze verwendet, um die Gesamtoberfläche eines Zylinders zu bestimmen. Das Postulat kann aufgeschlüsselt werden, um eine allgemeine Formel für alle rechten Zylinder zu erstellen.
A = 2B + L

Beachte, dass die Grundfläche, B, eines jeden Zylinders ist: B = πr2
Die Seitenfläche, L, für jeden Zylinder ist:
L=\text{Breite der Seitenfläche}\cdot\text{Höhe des Zylinders}\
L=\text{Umfang der Grundfläche}\cdot\text{Höhe des Zylinders}\\
L=2\pi{r}\cdot{h}\
Setzt man die beiden Gleichungen zusammen, erhält man:
Das Herausrechnen von a aus der Gleichung ergibt:
Der Flächeninhalt eines rechten Zylinders: Ein rechtwinkliger Zylinder mit dem Radius r und der Höhe h kann ausgedrückt werden als:
A = 2πr2 + 2πrh
oder:
A = 2πr(r + h)
Mit diesen Formeln kann man den Flächeninhalt eines beliebigen rechtwinkligen Zylinders bestimmen.
Beispiel 5
Bestimme mit der Formel den Flächeninhalt des Zylinders.
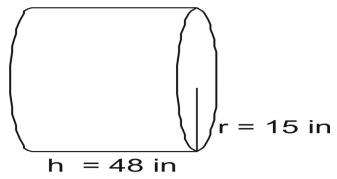
Schreibe die Formel, setze die Werte ein und löse.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ square inches}\
Beispiel 6
Bestimmen Sie den Flächeninhalt des Zylinders.
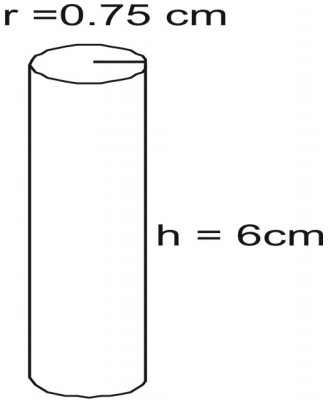
Schreibe die Formel, setze die Werte ein und löse.
A=2\pi{r}(r+h)\\
A=2(3.14)(0.75)\\
A=31.7925\text{ square inches}\
Beispiel 7
Bestimmen Sie die Höhe eines Zylinders, der einen Radius von 4cm und eine Oberfläche von 226,08 qcm hat.
Schreiben Sie die Formel mit den gegebenen Informationen und lösen Sie für h.
A=2\pi{r}(r+h)\\
226.08=2(3.14)(4)\\
226.08=25.12\\
226.08=100.48+25.12h\\
5=h\\
Kugeln
Eine Kugel ist eine dreidimensionale Figur, die die Form einer Kugel hat.

Kugeln können auf drei Arten charakterisiert werden.
- Eine Kugel ist die Menge aller Punkte, die in einem festen Abstand r von einem einzigen Mittelpunkt O liegen.
- Eine Kugel ist die Fläche, die entsteht, wenn ein Kreis um einen seiner Durchmesser gedreht wird.
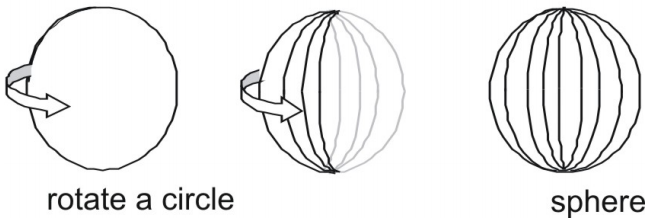
Flächeninhalt einer Kugel
Die Formel für den Flächeninhalt einer Kugel kann man durch Messungen an Kugeln und Zylindern herleiten. Hier zeigen wir eine Kugel mit einem Radius von 3 und einen rechten Zylinder mit einem Radius und einer Höhe von 3 und drücken den Flächeninhalt in π aus.
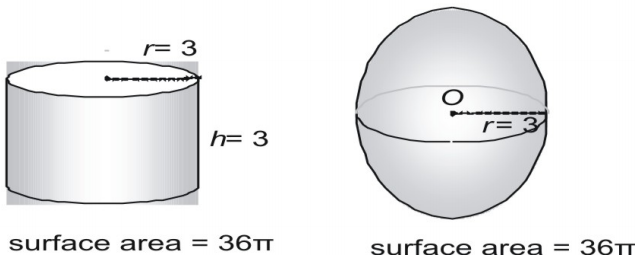
Nun versuchen wir ein größeres Paar und drücken den Flächeninhalt in Dezimalform aus.
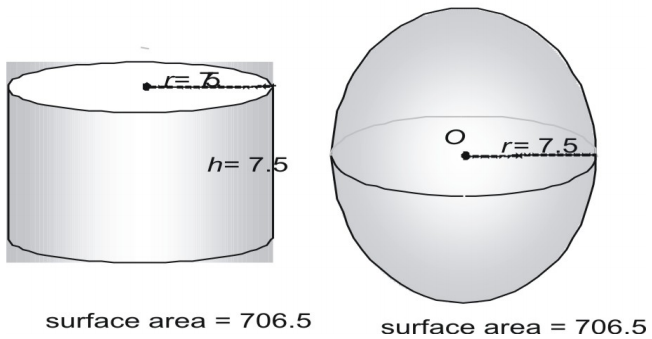
Betrachte ein drittes Paar.
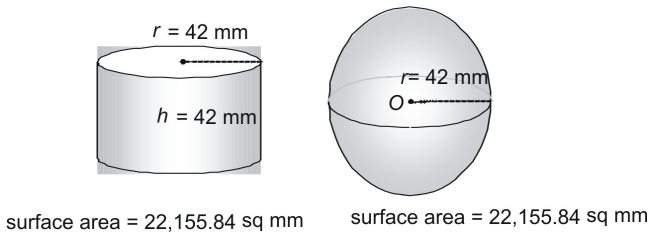
Ist es ein Zufall, dass eine Kugel und ein Zylinder, dessen Radius und Höhe gleich dem Radius der Kugel sind, genau den gleichen Flächeninhalt haben? Ganz und gar nicht! Tatsächlich verwendeten die alten Griechen eine Methode, die zeigte, dass die folgende Formel verwendet werden kann, um die Oberfläche jeder Kugel (oder jedes Zylinders, in dem ) zu finden.
Beispiel 8
Bestimmen Sie den Oberflächenbereich einer Kugel mit einem Radius von 14 Fuß.
Verwenden Sie die Formel.
A=4\pi{r}^2\
A=4\pi(14)^2\\
A=4\pi(196)\
A=784\pi\
2461.76\text{ Quadratfuß unter Verwendung von }3.14\text{ für }\pi\
Beispiel 9
Bestimmen Sie den Flächeninhalt der folgenden Figur in Form von π.
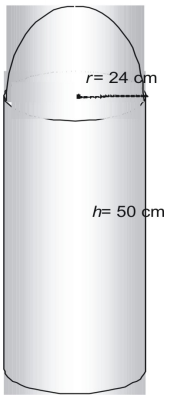
Die Figur besteht aus einer Halbkugel und einem Zylinder ohne Spitze.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half Kugel})=2\pi(576)\\
A(\text{Halbkugel})=1152\pi\text{Quadrat cm}\\
Bestimmen Sie nun die Fläche des Zylinders ohne seine Spitze.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, ist die Gesamtoberfläche 1152\pi+2976\pi=4128\pi\
Übungsaufgaben
- Bestimme den Radius der Kugel, die ein Volumen von 335 cm3 hat.
- Bestimme die Oberfläche und das Volumen dieser Form:

- Der Radius einer Kugel ist 4. Bestimme ihr Volumen und ihre Gesamtoberfläche.
- Eine Kugel hat einen Radius von 5. Ein rechter Zylinder mit dem gleichen Radius hat das gleiche Volumen. Finde die Höhe und die Gesamtoberfläche des Zylinders.
- Kugel: Volumen = 296 cm3. Finde den Durchmesser.
- Kugel: Fläche ist 179 in2. Finde den Radius.
- Tennisbälle mit einem Durchmesser von 3,5 Zoll werden in Dosen zu drei Stück verkauft. Die Dose ist ein Zylinder. Angenommen, die Bälle berühren die Dose an den Seiten, oben und unten. Wie groß ist das Volumen des Raums, der nicht von den Tennisbällen eingenommen wird?
- Eine Kugel hat eine Oberfläche von 36π in2. Finde ihr Volumen.
- Eine riesige Schaufel, die von einem Kran bedient wird, hat die Form einer Halbkugel mit dem Radius = 21 Zoll. Die Schaufel ist mit geschmolzenem, heißem Stahl gefüllt. Wenn der Stahl in einen zylindrischen Vorratstank mit einem Radius von 28 Zoll gegossen wird, steigt der geschmolzene Stahl bis zu einer Höhe von wie viel Zoll auf?
Antworten
Beachte, dass diese Aufgaben π und nicht 3,14 verwenden.
- 1. Radius = 4.31 cm
- Oberfläche = 706.86 cm2
Volumen = 1767.15 cm3 - Volumen = 268.08 Einheiten3
Oberfläche = 201.06 Einheiten2 - Höhe = 20/3 Einheiten Gesamtoberfläche = 366.52 Einheiten2
- Durchmesser = 8.27cm
- Radius = 3.77 Zoll
- Volumen des Zylinders = 32,16π in3 Volumen der Tennisbälle = 21,44π in3
Volumen des von den Tennisbällen nicht eingenommenen Raums = 33,68 in3 - Volumen = 113,10 in3
- Höhe des geschmolzenen Stahls im Zylinder beträgt 7,88 Zoll



