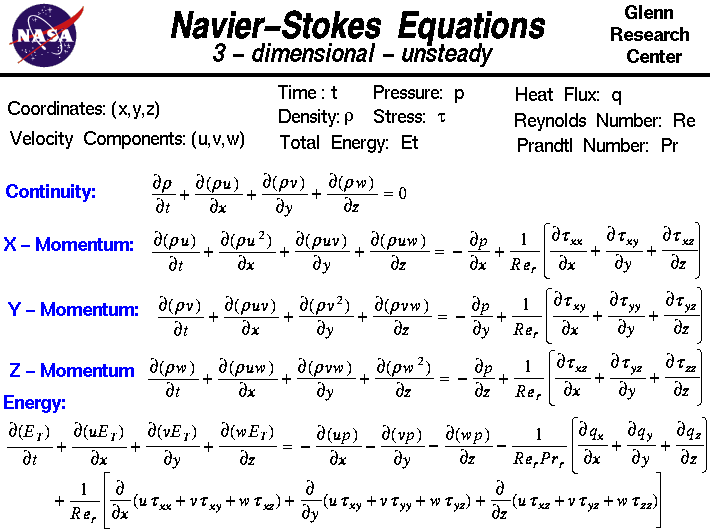
Auf dieser Folie zeigen wir die dreidimensionale instationäre Form der Navier-Stokes-Gleichungen.Diese Gleichungen beschreiben, wie Geschwindigkeit, Druck, Temperatur und Dichte eines sich bewegenden Fluids zusammenhängen.Die Gleichungen wurden unabhängig voneinander von G.G. Stokes in England und M. Navier in Frankreich Anfang des 19. Navier, in Frankreich, in den frühen 1800er Jahren abgeleitet. Die Gleichungen sind Erweiterungen der Euler-Gleichungen und umfassen die Auswirkungen der Viskosität auf die Strömung. Diese Gleichungen sind sehr komplex, aber Studenten der Ingenieurwissenschaften wird beigebracht, wie man sie in einem Prozess ableitet, der der Ableitung sehr ähnlich ist, die wir auf der Webseite über die Erhaltung des Impulses vorstellen.
Die Gleichungen sind ein Satz gekoppelter Differentialgleichungen und könnten theoretisch für ein gegebenes Strömungsproblem mit Methoden aus der Infinitesimalrechnung gelöst werden.In der Praxis sind diese Gleichungen jedoch zu schwierig, um sie analytisch zu lösen.In der Vergangenheit haben Ingenieure weitere Annäherungen und Vereinfachungen an den Gleichungssatz vorgenommen, bis sie eine Gruppe von Gleichungen hatten, die sie lösen konnten.In jüngster Zeit wurden Hochgeschwindigkeitsrechner eingesetzt, um Annäherungen an die Gleichungen mit einer Vielzahl von Techniken wie Finite-Differenzen-, Finite-Volumen-, Finite-Elemente- und Spektralmethoden zu lösen.Dieser Bereich wird als Computational Fluid Dynamics oder CFD bezeichnet.
Die Navier-Stokes-Gleichungen bestehen aus einer zeitabhängigen Kontinuitätsgleichung für die Erhaltung der Masse, drei zeitabhängigen Gleichungen für die Erhaltung der Momente und einer zeitabhängigen Gleichung für die Erhaltung der Energie.Es gibt vier unabhängige Variablen in dem Problem, die x-, y- und z-Raumkoordinaten eines Bereichs und die Zeit t. Es gibt sechs abhängige Variablen: den Druck p, die Dichte r und die Temperatur T (die über die Gesamtenergie Et in der Energiegleichung enthalten ist) sowie drei Komponenten des Geschwindigkeitsvektors: die Komponente u in x-Richtung, die Komponente v in y-Richtung und die Komponente w in z-Richtung. Alle abhängigen Variablen sind Funktionen von allen vier unabhängigen Variablen.Bei den Differentialgleichungen handelt es sich also um partielle Differentialgleichungen und nicht um gewöhnliche Differentialgleichungen, wie man sie im Anfangsunterricht der Analysis lernt.
Sie werden feststellen, dass das Differentialsymbol anders ist als das übliche „d /dt“ oder „d /dx“, das Sie bei gewöhnlichen Differentialgleichungen sehen. Das Symbol“
“ wird verwendet, um partielle Ableitungen zu kennzeichnen.Das Symbol zeigt an, dass wir alle unabhängigen Variablen festhalten müssen, mit Ausnahme der Variablen neben dem Symbol, wenn wir eine Ableitung berechnen. Die Gleichungen lauten:
Kontinuität: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energie: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
wobei Re die Reynolds-Zahl ist, die ein Ähnlichkeitsparameter ist, der das Verhältnis der Skalierung der Trägheit der Strömung zu den viskosen Kräften in der Strömung darstellt. Die q-Variablen sind die Komponenten des Wärmestroms und Pr ist die Prandtl-Zahl, ein Ähnlichkeitsparameter, der das Verhältnis der viskosen Spannungen zu den thermischen Spannungen angibt.Die tau-Variablen sind Komponenten des Spannungstensors.Ein Tensor entsteht, wenn man zwei Vektoren auf eine bestimmte Weise multipliziert. Unser Geschwindigkeitsvektor hat drei Komponenten, der Spannungstensor hat neun Komponenten. Jede Komponente des Spannungstensors ist selbst eine zweite Ableitung der Geschwindigkeitskomponenten.
Die Terme auf der linken Seite der Impulsgleichungen werden als Konvektionsterme der Gleichungen bezeichnet.Konvektion ist ein physikalischer Vorgang, der in einer Gasströmung auftritt, bei dem eine Eigenschaft durch die geordnete Bewegung der Strömung transportiert wird.Die Terme auf der rechten Seite der Impulsgleichungen, die mit der inversen Reynoldszahl multipliziert werden, werden als Diffusionsterme bezeichnet.Diffusionist ein physikalischer Vorgang, der in einer Gasströmung auftritt, bei dem eine Eigenschaft durch die zufällige Bewegung der Gasmoleküle transportiert wird.Diffusion hängt mit dem Spannungstensor und der Viskosität des Gases zusammen. Die Euler-Gleichungen enthalten nur die Konvektionsterme der Navier-Stokes-Gleichungen und können daher keine Grenzschichten modellieren. Es gibt eine spezielle Vereinfachung der Navier-Stokes-Gleichungen, die Grenzschichtströmungen beschreiben.
Beachten Sie, dass alle abhängigen Variablen in jeder Gleichung vorkommen.Um ein Strömungsproblem zu lösen, müssen Sie alle fünf Gleichungen gleichzeitig lösen; deshalb nennen wir dies ein gekoppeltes Gleichungssystem.Es gibt tatsächlich noch einige andere Gleichungen, die zur Lösung dieses Systems erforderlich sind. Wir zeigen nur fünf Gleichungen für sechs Unbekannte. Eine Zustandsgleichung gibt den Druck, die Temperatur und die Dichte des Gases an und wir müssen alle Terme des Spannungstensors angeben.
Aktivitäten:
Führungen
Navigation ..
Anfängerhandbuch Startseite