Eine Grenzschicht ist eine dünne Schicht eines viskosen Fluids in der Nähe der festen Oberfläche einer Wand, die mit einer sich bewegenden Strömung in Kontakt steht, in der (innerhalb ihrer Dicke δ) die Strömungsgeschwindigkeit von Null an der Wand (wo die Strömung aufgrund ihrer Viskosität an der Wand „klebt“) bis zu Ue an der Grenze variiert, was ungefähr (innerhalb eines Fehlers von 1 %) der Geschwindigkeit der freien Strömung entspricht (siehe Abbildung 1). Streng genommen ist der Wert von δ ein willkürlicher Wert, da die Reibungskraft, die von der molekularen Wechselwirkung zwischen Flüssigkeit und Festkörper abhängt, mit dem Abstand von der Wand abnimmt und im Unendlichen gleich Null wird.
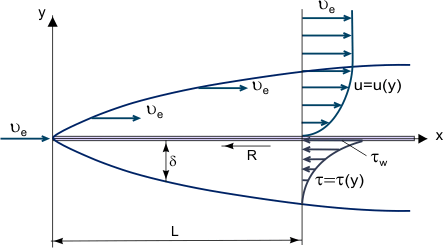
Abbildung 1. Wachstum einer Grenzschicht auf einer ebenen Platte.
Das grundlegende Konzept der Grenzschicht wurde von L. Prandtl (1904) vorgeschlagen, es definiert die Grenzschicht als eine Flüssigkeitsschicht, die sich in Strömungen mit sehr hohen Reynoldszahlen Re entwickelt, d.h. mit relativ geringer Viskosität im Vergleich zu den Trägheitskräften. Dies wird beobachtet, wenn Körper einem Luftstrom mit hoher Geschwindigkeit ausgesetzt sind oder wenn Körper sehr groß sind und die Geschwindigkeit des Luftstroms mäßig ist. In diesem Fall kann in einer relativ dünnen Grenzschicht die Reibungsschubspannung (viskose Scherkraft): τ = η (wobei η die dynamische Viskosität ist; u = u(y) – „Profil“ der Längsgeschwindigkeitskomponente der Grenzschicht, siehe Abbildung 1) sehr groß sein; insbesondere an der Wand, wo u = 0 und τw = ηw, obwohl die Viskosität selbst eher klein sein kann.
Es ist möglich, die Reibungskräfte außerhalb der Grenzschicht (im Vergleich zu den Trägheitskräften) zu vernachlässigen und auf der Grundlage des Prandtl’schen Konzepts zwei Strömungsgebiete zu betrachten: die Grenzschicht, in der die Reibungseffekte groß sind, und den nahezu unviskosen Strömungskern. Unter der Voraussetzung, dass die Grenzschicht eine sehr dünne Schicht ist (δ << L, wobei L die charakteristische lineare Abmessung des Körpers, über den die Strömung verläuft, oder des Kanals, in dem die Strömung stattfindet, ist und ihre Dicke mit zunehmendem Re abnimmt, Abbildung 1), kann man die Größenordnung der Grenzschichtdicke anhand der folgenden Beziehung abschätzen:
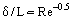
Fliegt z.B. ein Flugzeug mit Ue = 400 km/h, so beträgt die Grenzschichtdicke an der Flügelhinterkante mit 1 m Sehne (Profillänge)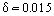 m. Wie experimentell festgestellt wurde, entwickelt sich im Einlaufbereich des Körpers eine laminare Grenzschicht. Unter dem Einfluss einiger destabilisierender Faktoren wird die Grenzschicht allmählich instabil und es findet ein Übergang der Grenzschicht zu einer turbulenten Strömung statt. Spezielle experimentelle Untersuchungen haben ergeben, dass es einen Übergangsbereich zwischen dem turbulenten und dem laminaren Bereich gibt. In einigen Fällen (z. B. bei hohem Turbulenzgrad der Außenströmung) wird die Grenzschicht unmittelbar stromabwärts des Stagnationspunktes der Strömung turbulent. Unter bestimmten Bedingungen, z. B. bei starkem Druckabfall, tritt bei beschleunigten turbulenten Strömungen ein umgekehrtes Phänomen auf, nämlich die Relaminarisierung der Strömung.
m. Wie experimentell festgestellt wurde, entwickelt sich im Einlaufbereich des Körpers eine laminare Grenzschicht. Unter dem Einfluss einiger destabilisierender Faktoren wird die Grenzschicht allmählich instabil und es findet ein Übergang der Grenzschicht zu einer turbulenten Strömung statt. Spezielle experimentelle Untersuchungen haben ergeben, dass es einen Übergangsbereich zwischen dem turbulenten und dem laminaren Bereich gibt. In einigen Fällen (z. B. bei hohem Turbulenzgrad der Außenströmung) wird die Grenzschicht unmittelbar stromabwärts des Stagnationspunktes der Strömung turbulent. Unter bestimmten Bedingungen, z. B. bei starkem Druckabfall, tritt bei beschleunigten turbulenten Strömungen ein umgekehrtes Phänomen auf, nämlich die Relaminarisierung der Strömung.
Trotz ihrer relativen Dünne ist die Grenzschicht sehr wichtig für die Einleitung von Prozessen der dynamischen Wechselwirkung zwischen der Strömung und dem Körper. Die Grenzschicht bestimmt den Luftwiderstand und den Auftrieb des fliegenden Fahrzeugs oder den Energieverlust für die Strömung in Kanälen (in diesem Fall eine hydrodynamische Grenzschicht, da es auch eine thermische Grenzschicht gibt, die die thermodynamische Wechselwirkung der Wärmeübertragung bestimmt).
Die Berechnung der Grenzschichtparameter basiert auf der Lösung von Gleichungen, die sich aus den Navier-Stokes-Gleichungen für viskose Flüssigkeitsbewegungen ergeben, die zunächst unter Berücksichtigung der Dünnheit der Grenzschicht erheblich vereinfacht werden.
Die von L. Prandtl vorgeschlagene Lösung ist im Wesentlichen der erste Term der Potenzreihenentwicklung der Navier-Stokes-Gleichung, wobei die Reihenentwicklung für Potenzen des dimensionslosen Parameters (δ/L) durchgeführt wird. Der kleinere Parameter in diesem Term ist in der Potenz Null, so dass die Grenzschichtgleichung die Nullnäherung in einer asymptotischen Expansion (bei großem Re) der Grenzschichtgleichung (asymptotische Lösung) ist.
Eine Transformation der Navier-Stokes-Gleichung in die Grenzschichtgleichungen kann durch Herleitung der Prandtl-Gleichung für eine laminare Grenzschicht in einer zweidimensionalen inkompressiblen Strömung ohne Körperkräfte demonstriert werden.
In diesem Fall lautet das System der Navier-Stokes-Gleichungen:

Nach Abschätzung der Größenordnung einiger Terme von Gl. (2) und unter Vernachlässigung kleiner Terme ergibt sich das System der Prandtl-Gleichungen für die laminare Grenzschicht:

wobei x, y Längs- und Seitenkoordinaten sind (Abbildung 1); v die Geschwindigkeitskomponente entlang der „y“-Achse ist; p der Druck; t die Zeit; und n die kinematische Viskosität.
Die Grenzschicht ist dünn und die Geschwindigkeit an ihrem äußeren Rand Ue kann ausreichend genau als die Geschwindigkeit einer idealen (nicht viskosen) Fluidströmung entlang der Wand bestimmt werden, die bis zur ersten Näherung berechnet wird, ohne die umgekehrte Wirkung der Grenzschicht auf die äußere Strömung zu berücksichtigen. Der longitudinale Druckgradient = (bei p(y) = const) in Gl. (3) kann aus der Eulerschen Bewegungsgleichung eines idealen Fluids dargestellt werden. Daraus ergeben sich die Prandtl-Gleichungen in ihrer endlichen Form zu schreiben als:

Dabei handelt es sich um ein System parabolischer, nichtlinearer partieller Differentialgleichungen zweiter Ordnung, die mit Anfangs- und Randbedingungen gelöst werden


Das Gleichungssystem (4) wird für aktuelle Werte der Geschwindigkeitskomponenten u und v geschrieben. Zur Verallgemeinerung der für die turbulente Strömung erhaltenen Gleichungen sollte die bekannte Beziehung zwischen aktuellen, gemittelten und pulsierenden Komponenten der Parameter turbulenter Strömungen verwendet werden. Zum Beispiel gibt es für Geschwindigkeitskomponenten Beziehungen, die die aktuellen u und v, die durchschnittlichen ū und und die pulsierenden u‘ und v‘ Komponenten verbinden:
und die pulsierenden u‘ und v‘ Komponenten verbinden:

Nach einigen Umstellungen ist es möglich, aus dem System (3) ein anderes Gleichungssystem zu erhalten, insbesondere für eine stationäre Strömung:
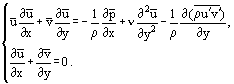
Unter Verwendung der folgenden Beziehung für die Reibungsschubspannung in der Grenzschicht:
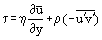
und unter Berücksichtigung, dass in der laminaren Grenzschicht u = u‘ und ist es möglich, die Prandtl-Gleichungen in einer Form umzuschreiben, die sowohl für laminare als auch für turbulente Strömungen gilt:
ist es möglich, die Prandtl-Gleichungen in einer Form umzuschreiben, die sowohl für laminare als auch für turbulente Strömungen gilt:
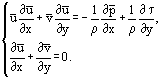
Die einfachsten Lösungen wurden für eine laminare Grenzschicht auf einer dünnen flachen Platte in einer zweidimensionalen, parallelen Strömung eines inkompressiblen Fluids erhalten (Abbildung 1). In diesem Fall erlaubt die Abschätzung der Größenordnung der Gleichungsterme: x ~ L, y ~ δ, δ ~ die Kombination der Variablen x und y in einer Beziehung
die Kombination der Variablen x und y in einer Beziehung

und die Lösung von Gl. (8) (bei dp/dx = 0) auf die Bestimmung der Abhängigkeiten von u und v von dem neuen Parameter ξ zu reduzieren. Andererseits ist es möglich, unter Verwendung der bekannten Beziehungen zwischen den Geschwindigkeitskomponenten u, v und der Stromfunktion ψ

eine gewöhnliche nichtlineare Differentialgleichung dritter Ordnung zu erhalten, anstelle des Systems der partiellen Differentialgleichungen (8)

Hier ist f(ξ) die unbekannte Funktion der Variablen ξ: f = ƒ =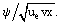
Die erste numerische Lösung von Gl. (10) wurde von Blasius (1908) unter Randbedingungen erhalten, die den physikalischen Bedingungen der Grenzschicht bei y = 0 entsprechen: u = 0, v = 0; bei y → ∞; u → Ue (Blasius-Grenzschicht).
Abbildung 2 vergleicht die Ergebnisse der Blasius-Lösung (durchgezogene Linie) mit experimentellen Daten. Anhand dieser Daten ist es möglich, die viskose Grenzschichtdicke zu bestimmen. Bei ξ  2,5, (u/Ue
2,5, (u/Ue 0,99) (Abbildung 2); folglich erhalten wir aus Gleichung (9):
0,99) (Abbildung 2); folglich erhalten wir aus Gleichung (9):

Abbildung 2.
Aus den numerischen Blasius-Berechnungen des Wertes der zweiten Ableitung der Funktion f(ξ) bei der Wandreibungsschubspannung ergibt sich in diesem Fall folgende Beziehung:

Die Reibungskraft R, die auf beiden Seiten der Platte der Länge L (Abbildung 1) wirkt, wird ebenfalls aus Gl. (11):

wie beim Reibungskoeffizienten für ebene Platten:
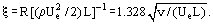
Trotz der Tatsache, dass die Prandtl-Gleichungen viel einfacher sind als die Navier-Stokes-Gleichungen, wurden ihre Lösungen nur für eine begrenzte Anzahl von Problemen erhalten. Für viele praktische Probleme ist es nicht notwendig, die Geschwindigkeitsprofile in der Grenzschicht zu bestimmen, sondern nur die Dicke und die Schubspannung. Diese Art von Information kann durch Lösen der integralen Impulsgleichung

Die integrale Beziehung (12) gilt sowohl für die laminare als auch für die turbulente Grenzschicht.
Funktionen, die a priori nicht bekannt sind, aber die Verteilung der Fluidparameter über die Schichtdicke δ charakterisieren, stehen unter dem Integral in Gl. (12). Und der Fehler bei der Berechnung des Integrals ist kleiner als der Fehler in der näherungsweise angenommenen Integrandenfunktion ρu = ρu(y). Dies schafft die Voraussetzungen für die Entwicklung von Näherungsmethoden zur Berechnung von Grenzschichtparametern, die weniger zeitaufwendig sind als die exakten Methoden zur Integration der Prandtl-Gleichungen. Das grundlegende Konzept wurde erstmals von T. von Karman vorgeschlagen, der eine solche willkürliche Schichtdicke δ*
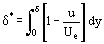
und eine Impulsverschiebungsdicke δ**
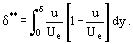
einführte, so dass wir Gleichung. (12) für eine zweidimensionale Grenzschicht eines inkompressiblen Fluids in:

Es gibt drei unbekannte Funktionen in Gl. (15), nämlich δ* = δ*(x), δ** = δ**(x) und τw = τw(x).
Die Lösung einer gewöhnlichen Differentialgleichung wie Gl. (15) erfordert in der Regel die Annahme (oder Darstellung) der Geschwindigkeitsverteilung (Geschwindigkeitsprofil) über die Grenzschichtdicke als Funktion einiger charakteristischer Parameter (Formparameter), und sie erfordert auch die Verwendung empirischer Daten über die Beziehung zwischen dem Reibungskoeffizienten Cf = 2τw/(ρU2e) und der beliebigen Dicke der Grenzschicht (Reibungsgesetz).
Es können einige eindeutige physikalische Erklärungen gegeben werden, soweit die Werte von δ* und δ** betroffen sind. Die Integralfunktion in Gl. (13) enthält nach Umformung einen Term (Ue – u), der die Geschwindigkeitsabnahme charakterisiert. Das Integral in Gl. (14) kann somit als Maß für die Abnahme der Strömungsgeschwindigkeit durch die Grenzschicht im Vergleich zur perfekten Strömung mit der Geschwindigkeit Ue betrachtet werden. Andererseits kann der Wert von δ* als Maß für die Abweichung entlang einer Normalen zur Wand (entlang der „y“-Achse) der äußeren Strömungslinie unter dem Einfluss von Reibungskräften betrachtet werden. Aus dieser Betrachtung der integralen Struktur von Gl. (14) lässt sich schließen, dass δ** die Impulsabnahme in der Grenzschicht unter dem Einfluss der Reibung charakterisiert.
Es gelten folgende Beziehungen:

wobei H der Formparameter des Grenzschicht-Geschwindigkeitsprofils ist. Zum Beispiel für die lineare Verteilung u = ky,
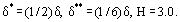
Zurzeit sind sogenannte semi-empirische Theorien zur Vorhersage turbulenter Grenzschichtparameter weit verbreitet. Dabei wird angenommen, dass die Gesamtreibungsspannung τ in einer turbulenten Grenzschicht eine Summe ist

Hier ist τT die zusätzliche (turbulente oder Reynolds) Reibungsspannung, insbesondere in einer inkompressiblen Strömung siehe Gleichung. (7).
siehe Gleichung. (7).
Diese Darstellung ist direkt mit dem System der Bewegungsgleichungen in der Grenzschicht (6) verbunden. In der kompressiblen Grenzschicht können die Dichtepulsationen als Ergebnis von Temperaturpulsationen angesehen werden

wobei β = (1/T) der volumetrische Expansionskoeffizient ist.
Zur Bestimmung von τT werden zusätzliche semi-empirische Hypothesen über den turbulenten Impulsübergang verwendet. Zum Beispiel,

wobei ηT der dynamische Koeffizient der turbulenten Viskosität ist, der von J. Boussinesq 1877 eingeführt wurde.
Auf der Grundlage des Konzepts der Ähnlichkeit von molekularem und turbulentem Austausch (Ähnlichkeitstheorie) führte Prandtl die Mischungsweg-Hypothese ein. Die Mischungslänge 1 ist der Weg, den ein endliches Flüssigkeitsvolumen („Mole“) von einer Schicht mittlerer Bewegung zu einer anderen zurücklegt, ohne seinen Impuls zu ändern. In Übereinstimmung mit dieser Bedingung leitete er eine Gleichung ab, die sich als grundlegend für die Grenzschichttheorie erwies:

Für den turbulenten Bereich der wandnahen Strömungsgrenzschicht, L. Prandtl betrachtete die Länge 1 proportional zu y

wobei κ eine empirische Konstante ist.
In der Nähe der Wand, wo ηT << η, ist die viskose Molekularreibung ein bestimmender Faktor. Die Dicke dieses Teils der Grenzschicht δ1, der als laminare oder viskose Unterschicht bezeichnet wird, beträgt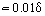 . Außerhalb der Unterschicht nimmt der Wert von ηT zu und erreicht mehrere Größenordnungen größer als η. Dementsprechend ist in diesem Bereich der Grenzschicht, der als turbulenter Kern bezeichnet wird, τT > 0 = η. Manchmal wird der turbulente Kern unterteilt in die Pufferzone, in der die laminare und die turbulente Reibung den gleichen Wert haben, und die entwickelte Zone, in der τT >> τ0 ist. Für diesen Bereich kann nach Integration von Gl. (18) und unter Berücksichtigung von Gl. (19) ein Ausdruck für das logarithmische Geschwindigkeitsprofil abgeleitet werden:
. Außerhalb der Unterschicht nimmt der Wert von ηT zu und erreicht mehrere Größenordnungen größer als η. Dementsprechend ist in diesem Bereich der Grenzschicht, der als turbulenter Kern bezeichnet wird, τT > 0 = η. Manchmal wird der turbulente Kern unterteilt in die Pufferzone, in der die laminare und die turbulente Reibung den gleichen Wert haben, und die entwickelte Zone, in der τT >> τ0 ist. Für diesen Bereich kann nach Integration von Gl. (18) und unter Berücksichtigung von Gl. (19) ein Ausdruck für das logarithmische Geschwindigkeitsprofil abgeleitet werden:
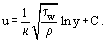
Wenn dimensionslose (oder universelle) Koordinaten verwendet werden.

wobei die sogenannte dynamische Geschwindigkeit (oder Reibungsgeschwindigkeit) ist, kann Gl. (20) kann in die folgende Form umgeschrieben werden:
die sogenannte dynamische Geschwindigkeit (oder Reibungsgeschwindigkeit) ist, kann Gl. (20) kann in die folgende Form umgeschrieben werden:
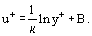
Die Darstellung der Geschwindigkeitsverteilung in universellen Koordinaten und die mathematischen Modelle für den turbulenten Viskositätskoeffizienten werden im Abschnitt über die turbulente Strömung ausführlicher behandelt.
Eine der aktuellen Versionen der semi-empirischen Theorie der turbulenten Grenzschicht, die von S. S. Kutateladze und A. I. Leontiev entwickelte semi-empirische Theorie der turbulenten Grenzschicht basiert auf der sogenannten asymptotischen Theorie der turbulenten Grenzschicht bei Re → ∞, bei der die Dicke der laminaren (viskosen) Unterschicht δ1 mit einer höheren Rate als δ abnimmt, wodurch (δ1/δ) → 0 wird.
Unter diesen Bedingungen entwickelt sich eine turbulente Grenzschicht mit „verschwindender Viskosität“. In dieser Schicht ist η → 0, aber nicht gleich Null, und in dieser Hinsicht unterscheidet sich die Schicht von einer perfekten Flüssigkeitsströmung. Das Konzept des relativen Reibungsgesetzes, das von S. S. Kutateladze und A. I. Leontiev (1990) eingeführt wurde, zeigt
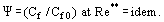
Das Gesetz ist definiert als das Verhältnis des Reibungskoeffizienten Cf für die betrachtete Bedingung zum Wert von Cf0 für „Standard“-Bedingungen auf einer flachen, undurchlässigen Platte, die von einer inkompressiblen, isothermen Strömung umströmt wird, wobei beide Koeffizienten für Re** = Ueδ**/ν erhalten werden. Es wird gezeigt, dass bei Re → ∞; η → 0; und Cf → 0 die relative Änderung des Reibungskoeffizienten unter dem Einfluss solcher Störfaktoren wie Druckgradient, Kompressibilität, Nicht-Isothermie, Injektion (Sog) durch eine poröse Wand usw. einen endlichen Wert hat.
Die für die Berechnung des Wertes von Ψ abgeleiteten Gleichungen haben eine wichtige Eigenschaft, die Ψ unabhängig von empirischen Konstanten der Turbulenz macht. Gemäß dem grundlegenden Konzept des integralen „Ansatzes“ wird die integrale Impulsgleichung umgewandelt in:
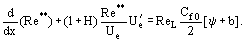
Hier, ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sind die Durchlässigkeitsparameter für den Fall, dass ein Gas mit der Dichte ρw durch eine durchlässige Wand mit der Geschwindigkeit vw eingeleitet wird. Zur Bestimmung der Funktion Re** = Re**
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sind die Durchlässigkeitsparameter für den Fall, dass ein Gas mit der Dichte ρw durch eine durchlässige Wand mit der Geschwindigkeit vw eingeleitet wird. Zur Bestimmung der Funktion Re** = Re** ist es notwendig, die Verteilung zu berechnen
ist es notwendig, die Verteilung zu berechnen Hierfür gilt das Prinzip der Überlagerung von Störfaktoren
Hierfür gilt das Prinzip der Überlagerung von Störfaktoren

In Gl. 24 stellt jeder Multiplikator das relative Reibungsgesetz dar, wobei die Wirkung eines der Faktoren berücksichtigt wird, darunter die Kompressibilität ΨM, die Temperatur- (oder Enthalpie-) Förderhöhe ΨT, die Einspritzung ΨB, der Druckgradient ΨP und andere.
Die Grundbegriffe der Grenzschicht schaffen die Voraussetzungen für die Erklärung solcher Phänomene wie Ablösung der Strömung von der Oberfläche unter dem Einfluss der Strömungsträgheit, Abbremsung der viskosen Strömung durch die Wand und ungünstiges Druckgefälle in Strömungsrichtung = 0 oder < 0.
Wenn der Druckgradient an der Oberfläche zwischen den Abschnitten „1-4“ ungünstig ist (siehe Abbildung 3), ändert sich die Geschwindigkeitsverteilung u = u(x,y) in der Grenzschicht allmählich; sie wird „weniger voll“, die Neigung in den Flüssigkeitsstrahlen, die näher an der Wand sind und weniger kinetische Energie besitzen, nimmt ab (siehe Formen des Geschwindigkeitsprofils in Abbildung 3), die weit stromabwärts in den Bereich des erhöhten Drucks eindringen. In einigen Abschnitten, z.B. im Abschnitt „4“, werden Fluidteilchen, die sich auf der Stromlinie „a-a“ (gestrichelte Linie in Abbildung 3) befinden, nachdem sie ihren Vorrat an kinetischer Energie vollständig aufgebraucht haben, abgebremst (ua = 0).
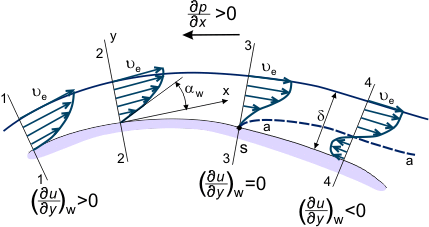
Abbildung 3. Grenzschicht in der Strömung über einer bedeckten Fläche.
Statischer Druck und Druckgradient variieren nicht über die Grenzschichtdicke. Daher beginnen Fluidteilchen, die sich näher an der Wand befinden als die Linie „a-a“ und noch weniger Energie besitzen, sich unter dem Einfluss des Druckgradienten im Abschnitt „4-4“ in die entgegengesetzte Richtung zu bewegen (siehe Abbildung 3). So ergibt sich die Beziehung:

Auf diese Weise ändert sich an einigen Stellen der Oberfläche das Geschwindigkeitsprofil. Diese Änderung ist dadurch gekennzeichnet, dass sich das Vorzeichen der Ableitung w von positiv (Abschnitt 2, Abbildung 3) zu negativ (Abschnitt 4) ändert. Natürlich ist es auch möglich, den Abschnitt zu definieren, in dem w = 0 ist (Abschnitt 3, Abbildung 3). Dieser Abschnitt wird als Grenzschichttrennungsabschnitt bezeichnet (der Punkt „S“ auf der Oberfläche dieses Abschnitts ist dementsprechend der Trennungspunkt). Er ist gekennzeichnet durch die Ausbildung einer Umströmungszone – die Umströmung des Körpers ist nicht mehr glatt, die Grenzschicht wird deutlich dicker und die äußeren Strömungslinien weichen von der Oberfläche des umströmten Körpers ab. Stromabwärts der Ablösungsstelle ist die statische Druckverteilung über die Schichtdicke nicht gleichmäßig und die statische Druckverteilung entlang der Oberfläche entspricht nicht der Druckverteilung in der äußeren, nicht viskosen Strömung.
Der Ablösung folgt die Ausbildung von Rückstromzonen und Verwirbelungen, in denen sich die von der äußeren Strömung zugeführte kinetische Energie unter dem Einfluss von Reibungskräften in Wärme umwandelt. Die Strömungsablösung, begleitet von Energiedissipation in den Rückstromwirbelzonen, führt zu unerwünschten Effekten wie der Erhöhung des Luftwiderstandes von fliegenden Fahrzeugen oder hydraulischen Verlusten in Kanälen.
Andererseits werden abgetrennte Strömungen in verschiedenen Vorrichtungen zur intensiven Vermischung von Fluiden eingesetzt (z.B. zur Verbesserung der Vermischung von Kraftstoff und Luft in Brennkammern von Motoren). Wenn viskose Flüssigkeiten in Kanälen mit variablem Querschnitt (wechselndes Druckgefälle) fließen, kann die Trennzone lokal sein, wenn auf den Diffusorabschnitt der Konfusorabschnitt folgt, in dem sich die abgetrennte Strömung wieder an der Oberfläche festsetzt (siehe Abbildung 4a). Wenn sich die Strömung von der Hinterkante des Körpers ablöst (z. B. von der Flügelhinterkante), bildet sich die so genannte Nachlaufströmung durch „verbindende“ Grenzschichten (siehe Abbildung 4b).
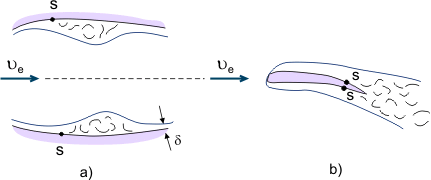
Abbildung 4. Grenzschichttrennungsphänomene.
Prandtl, L. (1904) Über Flüssigkeitsbewegungsbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Kutateladze, S. S. und Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.