
Fern
Tässä on tuore kysymys lukija Pehriltä Ruotsista:
Hei,
Ensinnäkin hieno sivusto. Love it.
Olen tutkinut polaarikoordinaatteja käsittelevää osiota toivoen voivani laajentaa tietämystäni tasakulmaspiraalista. Vuorovaikutteiset työkalut ovat loistavia, vaikka minulla on vaikeuksia johtaa tarkkaa matemaattista ratkaisua sille, miksi kultaisen spiraalin tuloksena saatava funktio on
r = ae^(b(theta))
Hieman taustaa Pehrin kysymykseen, katso:
Polaarikoordinaatit, käyrät polaarikoordinaateissa ja tasakulmainen spiraali
Spiraalit ovat yleisiä luonnossa, ja ne ovat inspiroineet matemaatikkoja vuosisatoja.

Aloen spiraali

Spiraaligalaksi NGC 5194
Logaritmiset spiraalit
Kultainen spiraali, josta Pehr kysyy, on logaritmisen spiraalin erikoistapaus.
Logaritmiset spiraalit kasvavat siten, että spiraalin keskipisteestä kulkevan viivan ja käyrän tangentin kulma kyseisessä pisteessä on vakio. Tämän vuoksi niitä kutsutaan myös ”tasakulmaisiksi” spiraaleiksi.
Voidaksemme nähdä, mitä tämä tarkoittaa, seuraavaan saniaiskuvaan merkityt 3 terävää kulmaa ovat noin 80°

Tasakulmainen saniainen
Käytämme tavallisesti funktioita polaarikoordinaatistossa, kun kuvaamme spiraaleja. Jos muuten käytämme tavallisia suorakulmaisia koordinaatteja, kaavoista tulee hyvin monimutkaisia.
Logaritmisen spiraalin kaava polaarikoordinaatteja käyttäen on:
r = aeθ cot b
joissa
r on etäisyys origosta (tai ”navasta”)
a on vakio
θ on kulma (radiaaneina) vaaka-akselista. Käyrän pisteen koordinaatit polaarikoordinaatistossa ovat siis (r, θ).
b on kulma (radiaaneissa – ”yhtäläinen” kulma), jonka spiraalin keskipisteestä lähtevä viiva muodostaa spiraalin tangentin kanssa. Yllä olevassa saniaisen tapauksessa b ≈ 1,4 radiaania (≈ 80°).
Johtuen tavasta, jolla määrittelimme logaritmisen spiraalin, vierekkäisen spiraaliparin kunkin spiraalihaaran keskipisteen etäisyyksien suhde on vakio.

Spiraalihaarat vakiosuhteessa
Suhde
etäisyys ensimmäiseen haaraan: etäisyys toiseen haaraan
= 29:69
≈ 0.42
Toinen suhde
etäisyys toiseen käsivarteen: etäisyys kolmanteen käsivarteen
= 69:154
≈ 0.45
Havaitsemme, että suhdeluvut ovat lähes samat. (Todellisessa logaritmisessa spiraalissa ne ovat täsmälleen samat. Saniaisen alkupisteen valitseminen ei ole eksaktia tiedettä)!
Kultainen spiraali
Kultainen spiraali on logaritmisen spiraalin erikoistapaus.
Voidaan kirjoittaa yleinen logaritminen spiraali funktioksi polaarikoordinaatistossa käyttäen t:tä seuraavasti:
r(t) = aet cot b
Huomautus: Normaalisti käytämme θ:tä riippumattomana muuttujana, mutta usein käytämme t:tä, koska voimme ajatella, että spiraali on jäljitettävissä ajan kuluessa. Sitä paitsi se on helpompi kirjoittaa!
Kultaisella spiraalilla on sellainen erikoisominaisuus, että jokaista 1/4-kierrosta (90° tai π/2 radiaaneina) kohden etäisyys spiraalin keskipisteestä kasvaa kultaisella suhteella φ = 1,6180.
Tämän tapahtuakseen cot b:n on otettava arvo (joka saadaan funktiomme ratkaisusta):
![]()
Käyttämällä tätä arvoa ja ottamalla yksinkertainen tapaus, jossa a = 1, funktiostamme tulee:
r(t) = e0.30635t
Käytämme tästä eteenpäin erinomaista ilmaista graafityökalua GeoGebraa.
Kultaisen spiraalin asettaminen GeoGebran avulla
Jos nyt kuvaamme funktiotamme GeoGebrassa tavallisilla suorakulmaisilla koordinaattiakseleilla, saamme seuraavan eksponentiaalikäyrän. Huomaa, että r kasvaa yhä nopeammin (se muuttuu jyrkemmäksi), kun t kasvaa.
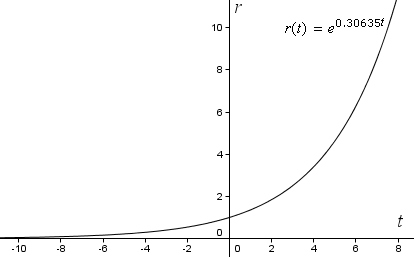
Mutta jotta näemme spiraalin, meidän on kuvattava käyrä polaarikoordinaattien avulla.
Muuttaaksemme polaarimuodon (joka meillä on) suorakulmaiseen muotoon (jota tarvitsemme kuvaajaa varten) Geogebrassa, meidän on asetettava ja kuvattava seuraava funktio:
a(t) = (r(t) cos(t), r(t) sin(t)).
Vaihdetaan muutama tärkeä arvo, jotta nähdään, mitä tämä lauseke tarkoittaa. Lähtökohtana on t = 0, jolloin saadaan käyrän alkupiste:
a(0) = (r(0) cos(0), r(0) sin(0)))
= (1×1, 1×0)
= (1, 0)
Se tarkoittaa siis, että lähdemme liikkeelle 1 yksikön päästä origosta positiivista x-akselia pitkin. Voit nähdä lähtöpisteen seuraavasta spiraalin kuvaajasta.
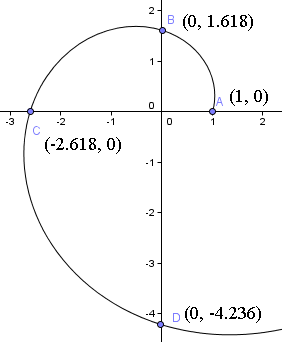
Seuraavaksi kierretään neljänneskierros ja havaitaan kohdassa t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1.618×0, 1.618×1)
= (0, 1.618)
Huomaa, että olemme nyt 1.618 yksikköä origosta y-akselia ylöspäin. Toisin sanoen φ = 1,6180 kertaa se etäisyys, josta lähdimme liikkeelle.
Muutama neljäsosakierroksen pyörähdys tuo meidät t = π, missä:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2.618×1, -2.618×0)
= (-2.618, 0)
Olemme nyt 2.618 yksikön etäisyydellä origosta negatiivista x-akselia pitkin eli φ = 1.6180 kertaa sen etäisyyden origosta, joka olimme viimeisellä neljänneskierroksella.
Huomautus:
φ2 = 2.6180
Voisimme laskea seuraavan sijaintimme negatiivista y-akselia pitkin kertomalla tämän viimeisen arvon φ = 1.6180:llä, jolloin saamme:
φ3 = 4.23606…
Siten spiraali leikkaa y-akselin pisteessä (0, -4.236).
Vielä yksi neljäsosakierros tuo meidät φ4 = 6.85410… yksikköön positiivisen y-akselin varrella, eli (6.854, 0).
Voitamme nähdä, että nämä arvot ovat oikeita yllä olevasta spiraalikäyrästämme.
Jos jatkamme eteenpäin, saamme spiraalin seuraavasti (tämä on 2 täyttä kierrosta eli 4π = 720°):
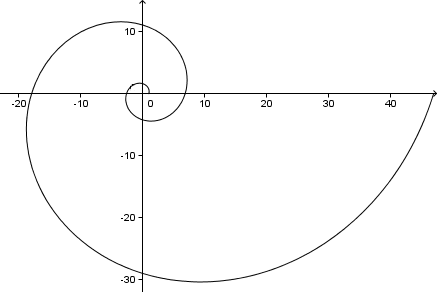
Sivuhuomautuksena, koska tässä tehtävässä
cot b = 0.30635
tällöin
b = arccot 0,30635 = 1,274 radiaania eli noin 73°
Tämä on kulma, jonka spiraalihaaramme muodostavat spiraalin keskipisteestä lähtevän viivan kanssa. Yllä olevasta kuvaajasta näet, että jokainen spiraalivarsi muodostaa x-akselin (ja y-akselin tai minkä tahansa keskipisteestä lähtevän viivan) kanssa 73°:n kulman.
Kultaisen spiraalin lähentäminen ympyrän kaaria käyttäen
Voimme saada aikaan spiraalin, joka näyttää melko samankaltaiselta kuin Kultainen spiraali, kun käytämme ympyrän ympyrän kaaria, jotka suurentuvat Kultaisen suhdeluvun verran, seuraavasti.
Aloitetaan 1×1-neliöstä ja piirretään kaari, keskipiste C, kahden kulman kautta siten, että neliön sivut ovat tangentteja kaareen (eli ne koskettavat vain kerran).
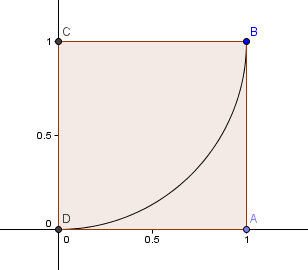
Seuraavaksi asetetaan neliö, jonka sivun pituus φ = 1.6180 ensimmäisen neliömme yläpuolelle ja rakennamme toisen ympyränkaaren, keskipiste E, kuten aiemmin:
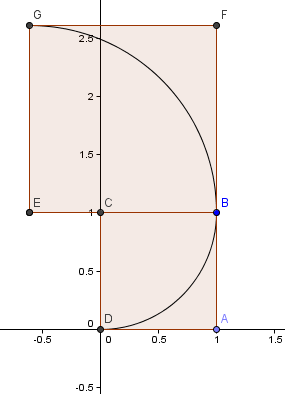
Seuraava neliömme menee vasemmalle ja sen sivut φ2 = 2.6180 = 1 + φ.
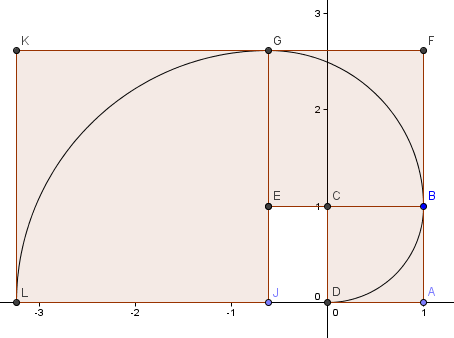
Jatkamme mallia (olemme käyneet vielä yhden kokonaisen kierroksen) ja saamme spiraalin, joka näyttää melko paljon samalta kuin aiemmin käyttämämme kultainen spiraali.
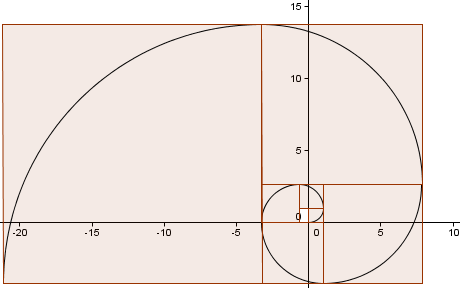
Kuinka lähellä approksimaatiomme on?
Wikipedian artikkelissa Kultainen spiraali on kuva, jossa väitetään, että yllä oleva spiraali ja Kultainen spiraali ovat muodoltaan hyvin lähellä.
Tässä on tuo kuva:
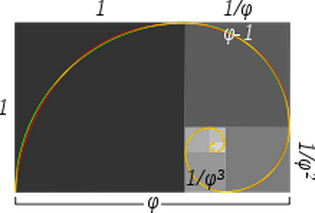
Kuvan kuvatekstissä sanotaan:
Likimääräinen ja todellinen kultainen spiraali: Vihreä spiraali on tehty kunkin neliön sisäpuolen tangenttisista neljännesympyröistä, kun taas punainen spiraali on kultainen spiraali, logaritmisen spiraalin erityinen tyyppi. Päällekkäiset osat näkyvät keltaisina. Suuremman neliön sivun pituus seuraavaan pienempään neliöön on kultasuhteen mukainen.
Voidaanko tämä luoda uudelleen ?
Oheisessa kuvassa punainen käyrä on ensimmäinen osa edellä konstruoimastamme kultaisesta spiraalista, kun taas vihreä käyrä perustuu neljänneskierroksen approksimaatioon, jota juuri työstimme.
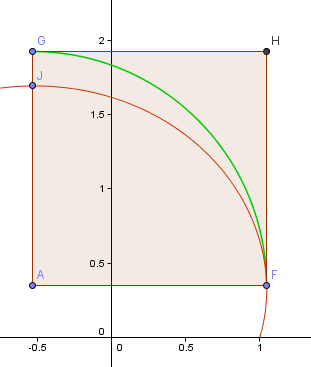
Piste F on spiraalin ”oikeanpuoleisin” piste, josta lähden liikkeelle neljänneksen kaarella. Piste J on spiraalin tämän osan korkein kohta.
Piste A on F:n ja J:n kautta kulkevien vaaka- ja pystysuorien viivojen leikkauspiste, ja siitä tulee kaareni keskipiste.
Nyt kaari GF ei ole lainkaan lähellä spiraalin siihen liittyvää osaa FJ.
Tehdään vielä yksi askel ja katsotaan, onko seuraava osa yhtään parempi.
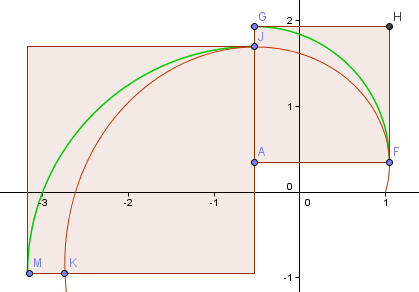
Kuten näette, se on huonompi (odotetusti, koska olemme siirtyneet kauemmas origosta ja spiraalin varsi kasvaa).
Tämä ei selvästikään tule koskaan toimimaan.
Mutta aiemmassa Golden Spiralissani käytin:
r(t) = e0.30635t
Vakiolla a, oli arvo 1.
Jos haluamme, että approksimointikaaremme sopivat hyvin todelliseen Kultaiseen spiraaliin, meidän on käytettävä arvoa (luultavasti ei yllättäen)
a = φ = 1.618103399..
Tällöin saamme seuraavat käyrät, jotka muistuttavat Wikipediassa olevaa kuvaajaa.
Punainen käyrä on Kultainen spiraali,
r(t) = 1.618013 e0.30635t
Vihreä käyrä on kokoelma ympyränkaaria.
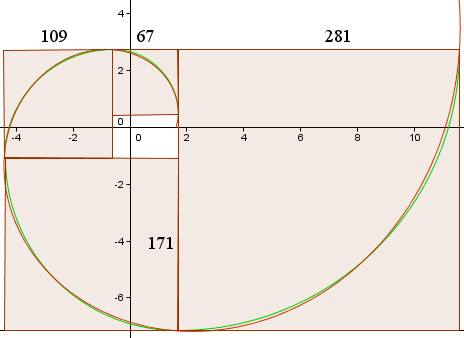
Neliöiden sivupituudet (pikseleinä) on esitetty ja näemme, että ne ovat suunnilleen suhteessa 1.618013…
Kultainen spiraali mediassa
From Wolfram’s Mathworld:
CBS-televisiokanavan Criminal Minds -rikosdraaman 4. kauden jaksossa ”Masterpiece” (2008) FBI:n käyttäytymisanalyysiyksikön agentit kohtaavat sarjamurhaajan, joka käyttää Fibonaccin numerosarjaa määrittääkseen uhrien lukumäärän jokaisessa tappojaksossaan. Tässä jaksossa hahmo tohtori Reid huomaa myös, että murhien paikat sijaitsevat kultaisen spiraalin kuvaajalla, ja spiraalin keskipisteeseen menemällä Reid voi määrittää tappajan tukikohdan sijainnin.
Tässä on lisää mielenkiintoista tietoa Wolfram’s Mathworldista:
Logaritminen spiraali
Nörteille – suunnittelussa käytetään kultaista spiraalia
Monien mielestä kultaista leikkaussuhdetta ja kultaista spiraalia käyttävät muotoilut miellyttävät silmää.
Jopa Twitter suunnitteli hiljattain etusivunsa uudelleen käyttäen kultaista spiraalia.
Tässä on hieno artikkeli kaverilta, joka on rakentanut kultaisen spiraalin ilman kuvia. (Lähinnä web-suunnittelusta kiinnostuneille)
Kultainen spiraali ilman kuvia – CSS:n ja jQueryn avulla
Kuten hän artikkelissa ehdottaa, myös norsun runko on lähellä kultaista spiraalia.

Norsunrunko – melkein Kultainen spiraali
Johtopäätös
Kultainen spiraali on mielenkiintoinen aihe – jota kannattaa seurata paitsi miellyttävien mallien myös niiden taustalla olevan mielenkiintoisen matematiikan vuoksi.
Toivottavasti tämä auttoi vastaamaan kysymykseesi, Pehr!