
Fern
Voici une question récente du lecteur Pehr en Suède :
Hi,
Tout d’abord, merveilleux site. Je l’adore.
J’ai étudié la section sur les coordonnées polaires en espérant élargir mes connaissances sur la spirale équiangulaire. Les outils interactifs sont formidables, bien que j’aie du mal à dériver la solution mathématique exacte pour savoir pourquoi la fonction résultante pour la spirale d’or est
r = ae^(b(thêta)).
Pour un peu de contexte sur la question de Pehr, voir:
Coordonnées polaires, courbes en coordonnées polaires et spirale équi-angulaire
Les spirales sont communes dans la nature et ont inspiré les mathématiciens pendant des siècles.

Spirale d’aloès

Galaxie spirale NGC 5194
Spirales logarithmiques
La spirale d’or sur laquelle s’interroge Pehr est un cas particulier de la spirale logarithmique.
Les spirales logarithmiques croissent de telle sorte que l’angle d’une ligne allant du centre de la spirale à la tangente à la courbe en ce point est constant. C’est pourquoi on les appelle aussi spirales « équi-angulaires ».
Pour voir ce que cela signifie, les 3 angles aigus marqués dans l’image suivante de la fougère font environ 80°

Fougère équi-angulaire
Nous utilisons normalement des fonctions en coordonnées polaires pour décrire les spirales. Sinon, si nous utilisons des coordonnées rectangulaires ordinaires, les formules deviennent très complexes.
La formule pour une spirale logarithmique utilisant des coordonnées polaires est:
r = aeθ cot b
où
r est la distance de l’origine (ou « pôle »)
a est une constante
θ est l’angle (en radians) par rapport à l’axe horizontal. Ainsi, les coordonnées d’un point sur la courbe en coordonnées polaires sont données par (r, θ).
b est l’angle (en radians – l’angle « égal ») que fait la ligne du centre de la spirale avec la tangente à la spirale. Dans le cas de la fougère ci-dessus, b ≈ 1,4 radians (≈ 80°).
Comme conséquence de la façon dont nous avons défini la spirale logarithmique, le rapport des distances du centre à chaque bras de spirale d’une paire adjacente est constant.

Bras de spirale à rapport constant
Le rapport
distance au premier bras : distance au second bras
= 29:69
≈ 0.42
L’autre rapport
distance au deuxième bras : distance au troisième bras
= 69:154
≈ 0,45
Nous voyons que les rapports sont presque les mêmes. (Dans une spirale logarithmique réelle, ils sont exactement les mêmes. Choisir le point de départ de la fougère n’est pas une science exacte).
Spirale d’or
La spirale d’or est un cas particulier de la spirale logarithmique.
On peut écrire la spirale logarithmique générale comme une fonction en coordonnées polaires utilisant t comme suit :
r(t) = aet cot b
Note : Normalement, on utilise θ pour la variable indépendante, mais on utilise souvent t car on peut penser que la spirale est tracée dans le temps. De plus, c’est plus facile à taper !
La spirale d’or a la propriété spéciale telle que pour chaque 1/4 de tour (90° ou π/2 en radians), la distance du centre de la spirale augmente du nombre d’or φ = 1,6180.
Pour que cela se produise, cot b doit prendre la valeur (qui provient de la résolution de notre fonction) :
![]()
En utilisant cette valeur, et en prenant le cas simple où a = 1, notre fonction devient :
r(t) = e0,30635t
Nous utiliserons à partir de maintenant l’excellent outil graphique gratuit GeoGebra.
Mise en place de la spirale d’or à l’aide de GeoGebra
Maintenant si nous graphions notre fonction sur des axes de coordonnées rectangulaires ordinaires dans GeoGebra, nous obtenons la courbe exponentielle suivante. Notez que r augmente à un taux toujours plus élevé (il devient plus raide) lorsque t augmente.
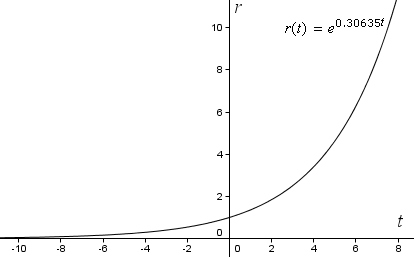
Mais pour voir une spirale, nous devons tracer la courbe en utilisant des coordonnées polaires.
Pour convertir la forme polaire (que nous avons) en forme rectangulaire (dont nous avons besoin pour le graphique) dans Geogebra, nous devons établir et tracer la fonction suivante :
a(t) = (r(t) cos(t), r(t) sin(t))
Substituons quelques valeurs importantes pour voir ce que signifie cette expression. En partant de t = 0, on obtient le point de départ de la courbe :
a(0) = (r(0) cos(0), r(0) sin(0)).
= (1×1, 1×0)
= (1, 0)
Cela signifie donc que nous commençons à 1 unité de l’origine le long de l’axe des x positif. Vous pouvez voir le point de départ dans le graphique suivant de la spirale.
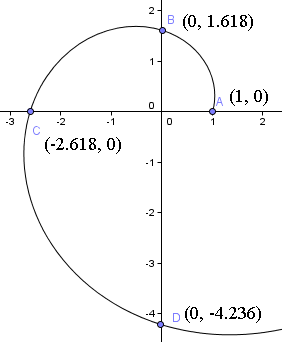
Puis, on tourne d’un quart de tour et on trouve à t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2)).
= (1,618×0, 1,618×1)
= (0, 1,618)
Notez que nous sommes maintenant à 1,618 unités de l’origine vers le haut de l’axe des y. C’est-à-dire, φ = 1,6180 fois la distance de départ.
Une autre rotation d’un quart de tour nous amène à t = π, où :
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Nous sommes maintenant à 2,618 unités de distance de l’origine le long de l’axe des x négatifs, soit φ = 1,6180 fois la distance de l’origine que nous avions au dernier quart de tour.
Note :
φ2 = 2,6180
Nous pourrions calculer notre prochaine position, le long de l’axe des y négatifs, en multipliant simplement cette dernière valeur par φ = 1,6180, ce qui nous donne :
φ3 = 4,23606….
Donc la spirale coupera l’axe des y à (0, -4,236).
Un quart de tour supplémentaire nous amènera à φ4 = 6,85410… unités le long de l’axe des y positif, soit (6,854, 0).
Nous pouvons voir que ces valeurs sont correctes sur notre graphique en spirale ci-dessus.
Si nous continuons, nous obtiendrons une spirale comme suit (cela représente 2 révolutions complètes, ou 4π = 720°):
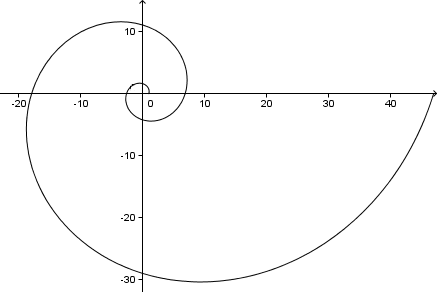
En passant, puisque dans ce problème
cot b = 0.30635
alors
b = arccot 0,30635 = 1,274 radians ou environ 73°
C’est l’angle que font nos bras en spirale avec une ligne partant du centre de la spirale. Vous pouvez voir sur le graphique ci-dessus que chaque bras de spirale fait un angle de 73° avec l’axe des x (et l’axe des y, ou toute ligne partant du centre).
Approximation de la Spirale d’Or en utilisant des arcs de cercle
Nous pouvons obtenir une spirale qui ressemble beaucoup à la Spirale d’Or en utilisant des arcs de cercles dont la taille augmente selon le Ratio d’Or, comme suit.
Nous commençons par un carré 1×1 et dessinons un arc, de centre C, passant par 2 coins tels que les côtés du carré soient tangents à l’arc (c’est-à-dire qu’ils ne se touchent qu’une seule fois).
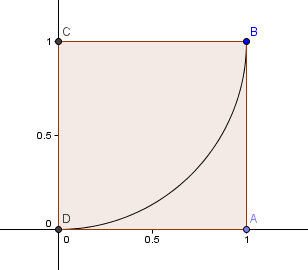
Puis, nous plaçons un carré de longueur de côté φ = 1.6180 au-dessus de notre premier carré et construisons un autre arc de cercle, de centre E, comme précédemment :
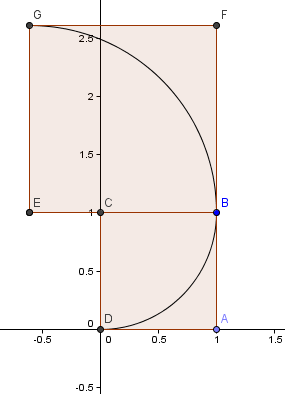
Notre prochain carré va à gauche et a des côtés φ2 = 2,6180 = 1 + φ.
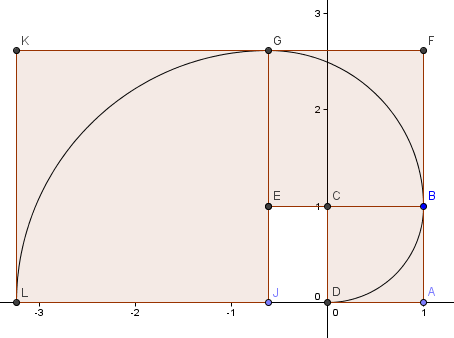
Nous continuons le schéma (nous avons fait un autre tour complet) et obtenons une spirale qui ressemble assez à notre spirale d’or de tout à l’heure.
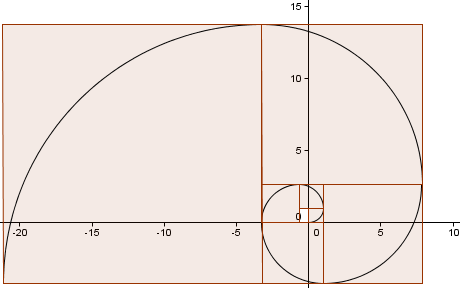
À quel point notre approximation est-elle proche ?
L’article de Wikipedia sur la spirale d’or a une image qui affirme que la spirale ci-dessus et la spirale d’or sont très proches en forme.
Voici cette image :
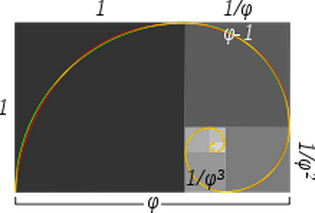
La légende de l’image indique :
Spirales dorées approximatives et vraies : la spirale verte est faite de quarts de cercle tangents à l’intérieur de chaque carré, tandis que la spirale rouge est une spirale dorée, un type spécial de spirale logarithmique. Les parties qui se chevauchent apparaissent en jaune. La longueur du côté d’un carré plus grand au carré plus petit suivant est dans le rapport d’or.
Pouvons-nous recréer ceci ?
Dans l’image ci-dessous, la courbe rouge est la première partie de la spirale d’or que nous avons construite ci-dessus, tandis que la courbe verte est basée sur l’approximation du quart de tour sur laquelle nous venons de travailler.
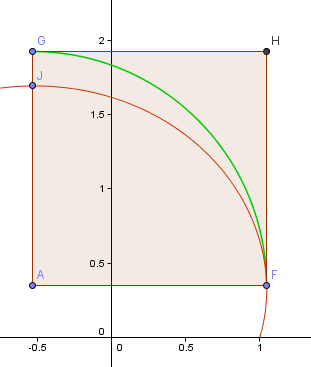
Le point F est le point « le plus à droite » de la spirale, qui sera mon point de départ pour l’arc du quart de tour. Le point J est le point le plus haut de cette portion de la spirale.
Le point A est l’intersection des lignes horizontale et verticale passant respectivement par F et J et ce sera le centre de mon arc.
Maintenant, l’arc GF n’est pas du tout proche de la portion connexe de la spirale FJ.
Faisons une autre étape et voyons si la partie suivante est meilleure.
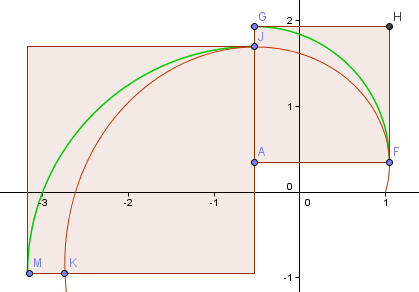
Comme vous pouvez le voir, c’est pire (comme prévu, puisque nous nous sommes éloignés de l’origine et que le bras de la spirale devient plus grand).
Certes, ça ne marchera jamais.
Cependant, dans ma spirale d’or précédente, j’utilisais :
r(t) = e0,30635t
La constante a, avait la valeur 1.
Si nous voulons que nos arcs d’approximation correspondent bien à la spirale d’or réelle, nous devons utiliser une valeur de (probablement pas surprenante)
a = φ = 1,618103399….
Cela nous donne les courbes suivantes, similaires au graphique de Wikipedia.
La courbe rouge est la Spirale d’Or,
r(t) = 1,618013 e0,30635t
La courbe verte est la collection d’arcs de cercle.
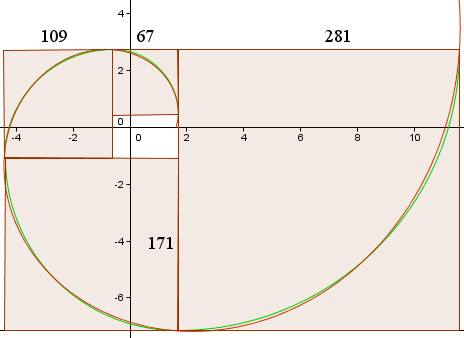
La longueur des côtés des carrés (en pixels) est indiquée et on voit qu’ils sont approximativement dans le rapport 1,618013…
Spirale dorée dans les médias
D’après Wolfram’s Mathworld :
Dans l’épisode « Masterpiece » (2008) de la saison 4 de la série policière de CBS-TV « Esprits criminels », les agents de l’unité d’analyse comportementale du FBI sont confrontés à un tueur en série qui utilise la séquence de nombres de Fibonacci pour déterminer le nombre de victimes pour chacun de ses épisodes meurtriers. Dans cet épisode, le personnage du Dr Reid remarque également que les emplacements des meurtres se trouvent sur le graphique d’une spirale dorée, et le fait de se rendre au centre de la spirale permet à Reid de déterminer l’emplacement de la base d’opérations du tueur.
Voici d’autres informations intéressantes tirées de Wolfram’s Mathworld :
Spirale logarithmique
Pour les geeks – design utilisant la spirale d’or
Il est estimé par beaucoup que les designs utilisant le ratio d’or et la spirale d’or sont agréables à l’œil.
Même Twitter a récemment redessiné sa page principale en utilisant la spirale d’or.
Voici un excellent article d’un gars qui a contruit une spirale d’or sans images. (Surtout pour ceux qui s’intéressent à la conception Web)
Spirale dorée sans images – en utilisant CSS et jQuery
Comme il le suggère dans l’article, la trompe d’un éléphant est également proche de la spirale dorée.

Tronc d’éléphant – presque une Spirale d’Or
Conclusion
La Spirale d’Or est un sujet intéressant – un sujet qui vaut la peine d’être poursuivi non seulement pour les conceptions agréables impliquées, mais aussi pour les mathématiques intéressantes derrière elles.
J’espère que cela aidera à répondre à votre question, Pehr !