インダクタとは｜EEP

インダクタという言葉は何度も耳にしたことがありますが、いったい何なのでしょう。それは、磁界にエネルギーを蓄積するように設計された受動素子です。このように、インダクタは電子機器や電力システムにおいて多くのアプリケーションを見つけることができます。

インダクタとは何か、どのように機能するか – 絶対に忘れてはならない事実 (photo credit: Tamara Kwan via Flickr)

電流の導体はすべて誘導特性を持ち、インダクタと見なされることがあります。

しかし、誘導効果を高めるために、実用的なインダクタは通常、図1に示すように、導電線を多数巻いた円筒形のコイルに形成されています。

もしインダクタに電流を流すと、インダクタにかかる電圧は電流の時間変化率に直接比例することがわかっています。ここでLはインダクタンスと呼ばれる比例定数であり、受動的な符号を用いると次の式(1)のようになる。インダクタンスの単位はヘンリー(H)で、アメリカの発明家ジョセフ・ヘンリー(1797-1878)にちなんで命名された。上式から明らかなように、1ヘンリーは1アンペアあたり1ボルト・秒に相当します。

上式から考えると、インダクタが端子間に電圧を持つためには、その電流は時間的に変化する必要があります。

インダクタンスとは、インダクタに流れる電流の変化に対してインダクタが抵抗力を示す性質のことで、単位はヘンリース(H)です。さまざまな形状のインダクタのインダクタンスを計算する公式は、電磁気学の理論から導かれ、標準的な電気工学のハンドブックに記載されています。

例えば、図1のインダクタ(ソレノイド)の場合、

ここで。

Nは巻数、
lは長さ、
Aは断面積、
mはコアの透磁率である。

この式から、コイルの巻数を増やす、コアに透磁率の高い材料を使う、断面積を大きくする、コイルの長さを短くするなどの方法で、インダクタンスを大きくできることがわかります

図2 各種インダクタ (a）ソレノイド型巻線インダクタ、（b）トロイダル・インダクタ、（c）チップ・インダクタ

コンデンサと同様に、市販のインダクタにもさまざまな値や種類がある。実用的なインダクタのインダクタンス値は、通信系の数マイクロヘンリー（mH）から電力系の数十ヘンリース（H）までが代表的である。固定式と可変式があります。コアは鉄、鋼、プラスチック、空気などでできている。

コイル、チョークという用語もインダクタに用いられる。

図3 – インダクタの回路記号を受動素子記号に従って示します。 (a）空芯、（b）鉄芯、（c）可変鉄芯

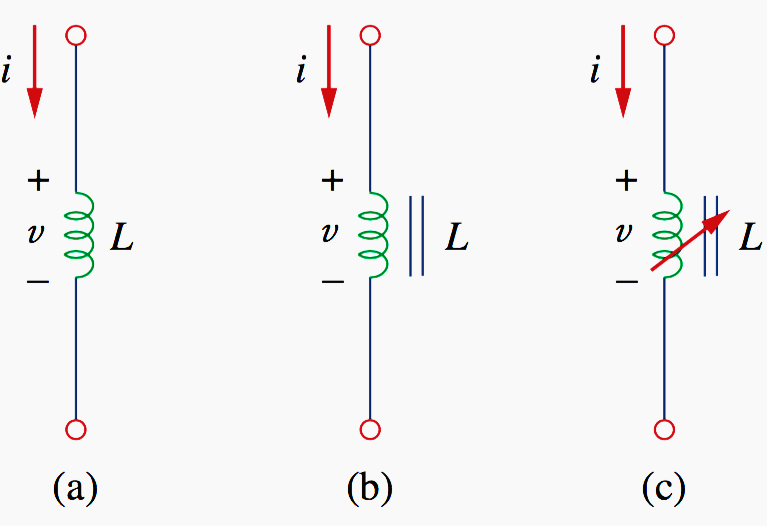
式（1）はインダクタの電圧-電流の関係である。図4は、インダクタンスが電流に依存しないインダクタの場合、この関係をグラフにしたものである。非線形インダクタの場合、インダクタンスが電流によって変化するため、式(1)のプロットは直線にならない。

式（1）から電流-電圧関係は、

積分すると次のように求まります。

ここでi（t0）は-∞t<までの総電流でi（-∞）=0とする。過去にインダクタに電流が流れない時期があったはずなので、i(-∞)とする考え方は実用的で合理的である。

インダクタはその磁界にエネルギーを蓄積するように設計されている。蓄えられたエネルギーは式(1)から求めることができる。インダクタに供給される電力は：

蓄えられるエネルギーは。

i(-∞)=0なので、

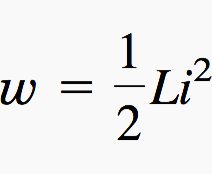
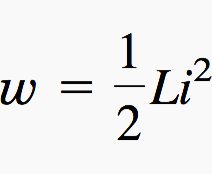
注 //

インダクターの重要な特性について以下に記しておく。

NOTE 1 //

式1より、電流が一定のとき、インダクタにかかる電圧はゼロであることに注意すること。

Thus, An inductor acts like a short circuit to DC.

NOTE 2 //

インダクタの重要な特性は、そこを流れる電流の変化に対する対抗性です。

式（1）によると、インダクタを流れる電流を不連続に変化させるには、無限の電圧が必要ですが、これは物理的に不可能です。例えば、インダクタに流れる電流は図5(a)のような形になりますが、現実には不連続性があるため図5(b)のような形にはなりません。しかし、インダクタにかかる電圧は急激に変化することがある。

図5 – インダクタに流れる電流。 (a) 許容、(b) 不可能。急激な変化は不可能

NOTE 3 //

理想のコンデンサーと同様に、理想的なインダクタはエネルギーを散逸させません。その中に蓄えられたエネルギーは、後で取り出すことができます。インダクタは、エネルギーを蓄積するときに回路から電力を受け取り、以前に蓄積したエネルギーを戻すときに回路に電力を供給します。

NOTE 4 //

理想的ではない実際のインダクタは、図 6 に示すように、かなりの抵抗成分を持ちます。これはインダクタが銅などの導電材料でできているためで、ある程度の抵抗があります。

この抵抗は巻線抵抗Rwと呼ばれ、インダクタのインダクタンスと直列で現れるのが特徴です。 Rwの存在によって、エネルギー蓄積デバイスであると同時にエネルギー散逸デバイスにもなる。 Rwは通常非常に小さいので、ほとんどの場合無視される。また、非理想的なインダクタには、導電性コイル間の容量結合による巻線容量Cwがあります。

Cw は非常に小さいので、高周波を除いてほとんどの場合、無視することができます。 396>

Who was Joseph Henry?

Joseph Henry (1797-1878) はアメリカの物理学者で、インダクタンスを発見し、電気モータを製作した人物である。 1936>

Joseph Henry (1797-1878), an American physicist, discovered inductance and constructed an electric motor

He was the first secretary of the Smithsonian Institution.ニューヨークのオルバニーで生まれて、オルバニーのアカデミーを卒業して1832から1846までプリンストン大で哲学を教えて、その後、アメリカン物理学者、インダクタンスと電動機を発見した。彼は電磁気学に関するいくつかの実験を行い、数千ポンドの重さの物体を持ち上げることのできる強力な電磁石を開発した。興味深いことに、ジョセフ・ヘンリーはファラデーより先に電磁誘導を発見したが、その成果を発表できなかった。

インダクタンスの単位であるヘンリーは、彼の名にちなんで命名された。

Free Press