圧力とは、ある平面上に作用するある点の単位面積あたりの法線力を表します。 静止状態の流体にはせん断応力が存在しないので、流体の圧力は方向とは無関係です。
静止状態の流体(液体または気体)の場合、垂直方向の圧力勾配は流体の比重にのみ依存します。
流体中の圧力が高さによってどのように変化するかは
Δp = – γ Δh (1)
ここで
Δp = 圧力変化 (Pa.), 6001>
Δh = 高さの変化 (m, in)
γ = 液体の比重 (N/m3, lb/ft3)
垂直方向の圧力勾配は負、つまり圧力は上方へ減少します。
比重
流体の比重は次のように表されます:
γ = ρ g (2)
where
ρ = 流体の密度 (kg/m3, slugs/ft3)
g=重力加速度 (9.81 m/s2, 32.174 ft/s2)
一般に、比重 – γ – は流体に対して一定である。 気体の場合、比重γは標高(および圧縮)により変化する。
静止流体が及ぼす圧力は、
- 流体の深さ
- 流体の密度
- 重力加速度
流体の静圧
圧縮不可能な液体では、二つの高さ間の圧力差は、こう表現することができる。
Δp = p2 – p1
= – γ (h2 – h1) (3)
where
p2 = level 2での圧力 (Pa, psi)
p1 = level 1での圧力(Pa。 psi)
h2 = レベル2 (m, ft)
h1 = レベル1 (m, ft)
(3) に変換することができる。
p = p1 – p2
= γ (h2 – h1) (4)
or
p1 – p2 = γ Δh (5)
where
h2 – h1 = 高度差 – 場所 h2 から h1 へ下がった深さ (m. m) ft)
or
p1 = γ Δh + p2 (6)
例-流体の圧力
水深10mでの絶対圧は、次のように計算できる。
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m) + (101.3 kPa)
=(98100 kg/ms2 or Pa)+(101300 Pa)
= 199400 Pa
= 199.4 kPa
ここで
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = 地表の圧力 = 大気圧 = 101.3 kPa
ゲージ圧は、p2 = 0
p1 = γ Δh + p2
= (1000kg/m3) (9.81m/s2) (10m)
= 98100 Pa
= 98.1 kPa
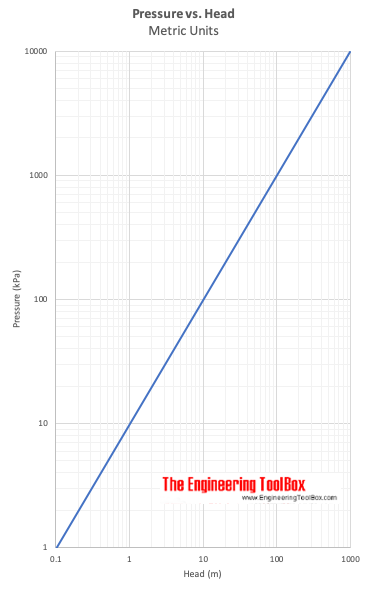
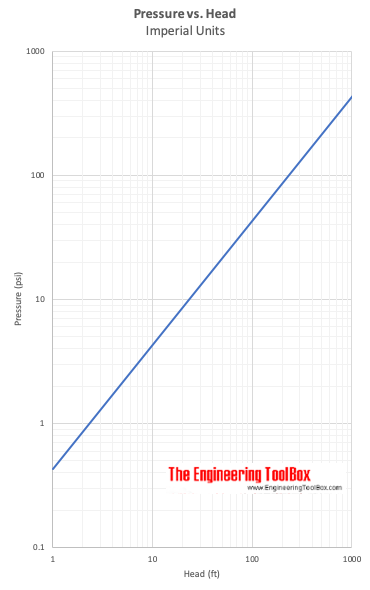
Pressure vs. Head
(6) は次のように変形できる。
Δh = (p2 – p1) / γ (7)
Δh express head – the height difference of a column of fluid of specific weight -γ – required to give a pressure difference Δp = p2 – p1.P1. (6001>
Δh = p2 – p1).
例-圧力対ヘッド
圧力差5psi(lbf/in2)は水中のヘッドに相当する
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11.6 ft of water
or head in Mercury
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0.85 ft of mercury
水の固有重量は62.1 ftです。4 (lb/ft3) で、水銀の比重は 847 (lb/ft3)
- Velocity – Dynamic Pressure vs. Head
です。