Free Press

スウェーデンの読者Pehrさんからの最近の質問を紹介します。

Hi,
First of all, wonderful site.
私は、等角螺旋の知識を広げたいと思い、極座標のセクションを勉強しています。 インタラクティブなツールは素晴らしいのですが、なぜ黄金螺旋の結果の関数が
r = ae^(b(theta)) なのか、正確な数学的解答を導き出すのに苦労しています。

Pehr の質問の背景については、以下を参照してください：

極座標、極座標の曲線と等角スパイラル

スパイラルは自然の中でよく見られ、数世紀にわたって数学者にインスピレーションを与えてきました。

Logarithmic Spirals

Pehrが求めている Golden Spiral は対数の特殊ケースである。

対数螺旋は螺旋の中心からその点での曲線の接線に向かう直線の角度が一定になるように成長する。 これが等角螺旋と呼ばれる所以である。

この意味を理解するために、次のシダの画像に記された3つの鋭角は約80°である

Equi-angular fern

我々は通常螺旋について述べるとき極座標による関数を使っている。 そうでないと、普通の直交座標を使った場合、式が非常に複雑になってしまう。

極座標を使った対数螺旋の式は次のようになります：

r = aeθ cot b

ここで

r は原点（または「極」）からの距離

a は定数

θ は水平軸からの角度（ラジアンで）であり、

r = aeθ cot bは水平軸からの距離

と同じです。

bは螺旋の中心からの線が螺旋の接線となす角度(ラジアン単位、「等角」)で、極座標では曲線上の点の座標は (r, θ) で与えられる。 上のシダの場合、b≒1.4ラジアン（≒80°）。

対数螺旋の定義方法の結果として、中心から隣接するペアの各螺旋腕までの距離の比は一定である。

一定の比での螺旋腕

第1腕までの距離：第2腕までの距離

= 29：69

≈ 0.42

もう一方の比率

二の腕までの距離：三の腕までの距離

= 69:154

≈ 0.45

ほとんど同じ比率になっていることが分かります。 (実際の対数螺旋では、全く同じになる。 シダの始点選びは厳密な科学ではありません！)

Golden Spiral

黄金螺旋は対数螺旋の特殊なケースです。

一般的な対数螺旋はtを使った極座標の関数として次のように書ける：

r(t) = aet cot b

注：通常、独立変数にはθを使うが、螺旋が時間的にたどれると考えることができるので、しばしばtを使うことができる。 それに、入力しやすいしね!

黄金螺旋は1/4回転（90°またはラジアンでπ/2）するごとに、螺旋の中心からの距離が黄金比φ=1.6180で増加するという特別な性質がある。

この値を使って、a = 1の単純な場合を考えると、私たちの関数は次のようになります。

r(t) = e0.30635t

ここからは無料の優れたグラフ作成ツールGeoGebraを使用することにします。

GeoGebraを使った黄金螺旋の設定

さて、GeoGebraで普通の長方形の座標軸に関数をグラフ化すると、次のような指数曲線が得られます。 tが大きくなるとrがどんどん大きくなる（急勾配になる）ことに注意してください。

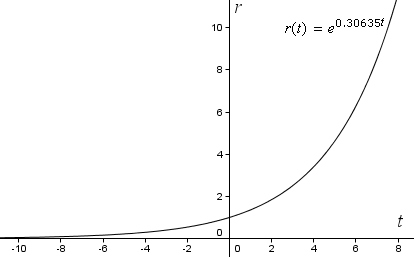
しかし、螺旋を見るには、極座標を使って曲線をグラフ化する必要があります。

Geogebraで極形式（これは私たちが得たもの）を直方体（これはグラフに必要）へと変換するには、次の関数を設定しグラフ化することが必要です。

a(t) = (r(t) cos(t), r(t) sin(t))

この式が何を意味するのか、重要な値をいくつか代入してみましょう。 t=0から始めると、曲線の始点が得られます。

a(0) = (r(0) cos(0), r(0) sin(0))

= (1×1, 1×0)

= (1, 0)

つまり、正のx軸に沿って原点から1単位スタートということですね。 次のような螺旋のグラフを見ると、その始点がわかります。

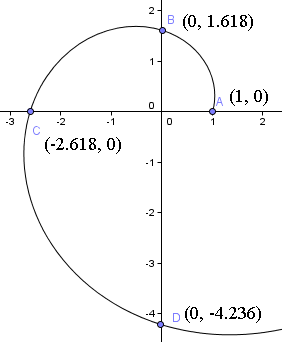
次に、1/4回転して、t = π/2で、

a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2)) が見つかります。

= (1.618×0, 1.618×1)

= (0, 1.618)

原点からY軸方向に1.618単位進んだことに注意してください。 つまり、φ＝スタート地点の距離の1.6180倍です。

さらに1/4回転すると、t = πになります。

a（π）＝（r（π）cos（π）、r（π）sin（π））。

= (-2.618×1, -2.618×0)

= (-2.618, 0)

現在、負のx軸に沿って原点から2.618ユニット離れており、最後の1/4回転時にあった原点からの距離の、φ= 1.6180 倍の距離にあります。

注：

φ2 = 2.6180

負のy軸に沿って次の位置を計算するには、この最後の値にφ = 1.6180 を掛ければよいので、

φ3 = 4.23606 … となります。

ですから、螺旋は(0, -4.236)でy軸を切ります。

さらに1/4回転するとφ4 = 6.85410… ユニット、つまり正のy軸に沿って(6.854、 0) になります。

上の螺旋グラフでこれらの値が正しいことが確認できます。

このまま進むと、次のような螺旋になります（これは完全な2回転、つまり4π=720°）：

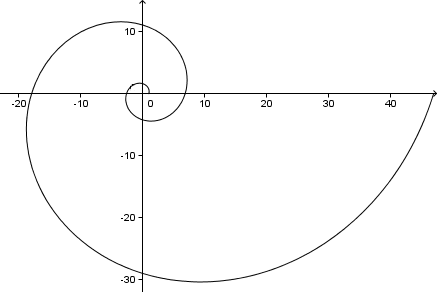余談ですが、この問題では

cot b = 0.なので、

cot b = 0.30635

then

b = arccot 0.30635 = 1.274 radians or around 73°

これが螺旋の中心からの線に対して、我々の螺旋腕が作る角度になるのです。 上のグラフで各螺旋の腕がx軸（とy軸、または中心からの任意の線）と73°の角度を作るのがわかる。

Approximating the Golden Spiral using arcs of a circle

次のように黄金比によって大きくなる円の円弧を使って、かなり黄金螺旋に近い螺旋を得ることが出来る。

まず1×1の正方形から始め、2つの角を中心Cとして、正方形の辺が円弧に接するように（つまり1度だけ接するように）円弧を描く。最初の正方形の上に6180を置き、先ほどと同様に中心Eで円弧を構成します。

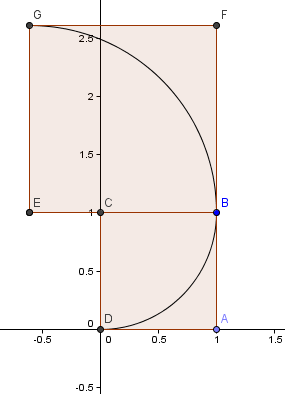
次の正方形は左側で、辺はφ2 = 2.6180 = 1 + φとします。

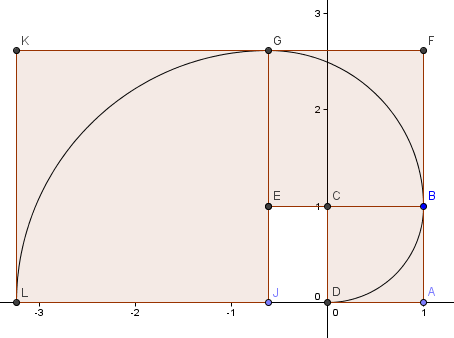
このパターンを続けると(もう一周しました)、先ほどの黄金螺旋とよく似た螺旋ができます。

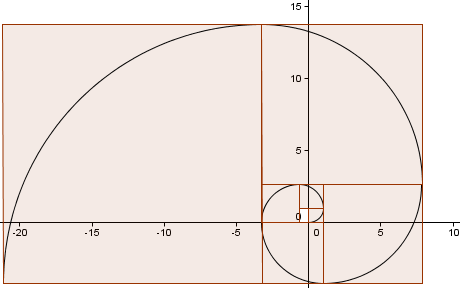
どのくらい近似できるか？

Wikipedia の Golden Spiral についての記事で、上のスパイラルと黄金螺旋は非常に近い形だとする画像があります。

Here’s that image:

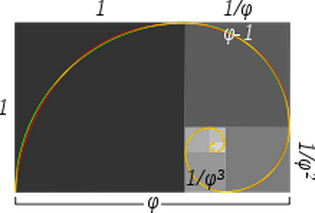
The caption states:

Approximate and true golden spirals: The green spiral is made from quarter-circles tangent to interior of each square, while the red spiral is a golden spiral, a special type of logarithmic spiral.近似的な螺線形は正方形の内側にある四角形で、赤い螺線形は対数の螺旋の特別なタイプである。 重なっている部分は黄色に見える。 大きい正方形の辺から次の小さい正方形までの長さは黄金比になる。

これを再現することはできるでしょうか？

下のイメージでは、赤いカーブは私たちが上で構築したゴールデンスパイラルの最初の部分であり、緑のカーブは私たちがちょうど取り組んでいた1/4回転の近似に基づいている。

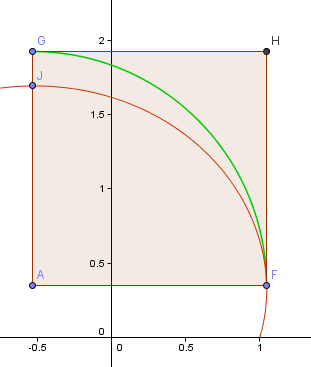F点はスパイラルの「右端」であり、これは1/4回転弧の私の出発点になる。 点Jはこの部分の最高点です。

点AはFとJをそれぞれ通る水平線と垂直線の交点で、ここが私の円弧の中心となります。

もう1ステップやって、次の部分が少しでも良くなるか見てみましょう。

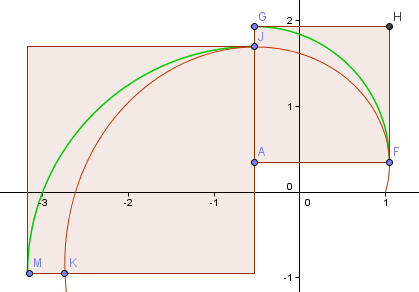見ての通り、悪くなっています（原点からさらに離れて、螺旋の腕が大きくなっているので、予想通りです）。

明らかに、これは決してうまくいきません。

しかし、私の以前のゴールデンスパイラルで私は使っていました。

r(t) = e0.30635t

定数aは値1であった。

もし私たちが近似円弧を実際の黄金螺旋にうまくフィットさせたいなら、（おそらく驚くことではありませんが）

a = φ = 1.618103399 という値を使用する必要があります…

これにより、Wikipediaのグラフに似た以下の曲線が得られる。

赤い曲線はゴールデンスパイラル、

r(t) = 1.618013 e0.30635t

緑の曲線は円弧の集合体である。

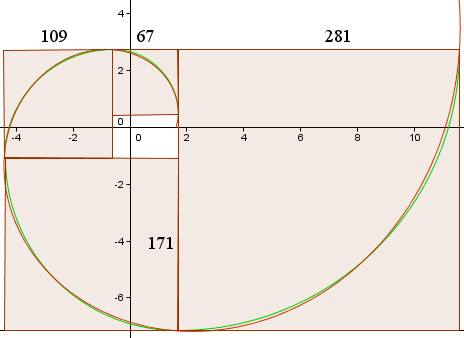
正方形の辺の長さ（ピクセル単位）を示しており、およそ1.618013の比率であることがわかる…

メディアにおける黄金螺旋

WolframのMathworldから。

CBS-TV の犯罪ドラマ「クリミナル マインド」のシーズン 4 エピソード「マスターピース」（2008）では、FBI 行動分析課の捜査官が、フィボナッチ数列を使って自分の殺害エピソードごとに犠牲者の数を決定する連続殺人犯に直面する場面で、フィボナッチ数列を使用することが判明しました。 このエピソードでは、登場人物の Reid 博士も、殺害の場所が黄金螺旋のグラフ上にあることに気づき、螺旋の中心に行くことで、Reid は殺人者の活動拠点の場所を決定することができます。

Logarithmic Spiral

For the geeks – design using Golden Spiral

黄金比と黄金螺旋を使ったデザインは目に楽しいと多くの人が信じています。

画像なしで黄金螺旋を構築した人による素晴らしい記事を紹介します。 (主に Web デザインに興味がある人向け)

Golden Spiral without images – using CSS and jQuery

記事の中で彼が示唆しているように、象の鼻も Golden Spiral に近いです。

Elephant trunk – almost a Golden Spiral

Conclusion

ゴールデン スパイラルは興味深いトピックで、楽しいデザインだけでなく、その背後にある興味深い数学も追求する価値があります。