Amortized analyse wordt gebruikt voor algoritmen die dure operaties hebben die slechts zelden voorkomen.

Amortized complexity analyse wordt het meest gebruikt bij datastructuren die een toestand hebben die tussen operaties door blijft bestaan.Het basisidee is dat een dure bewerking de toestand zodanig kan veranderen dat het ergste geval zich gedurende lange tijd niet meer kan voordoen, zodat de kosten worden afgeschreven.
Zie T1, T2, …, Tk als de complexiteit van een reeks bewerkingen op een gegevensstructuur. De afgeschreven complexiteit van een enkele bewerking in deze reeks is(T1 + T2 + …+ Tk) / k.
Voorbeeld: een dynamische array
In een dynamische array worden elementen opgeslagen aan het begin van een onderliggende vaste array, en de resterende posities zijn ongebruikt.
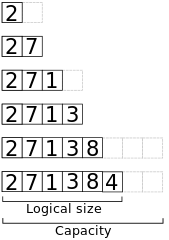
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Hier ziet u een overzicht van het geheugen bij het toevoegen van de elementen 2, 7, 1, 3, 8, 4aan een initieel lege array met capaciteit 2.
Worst-case tijd
De worst-case tijdcomplexiteit voor het appen van een element naar een array van lengte n, met behulp van dit algoritme, is Θ(n).Als de array vol is, wijst het algoritme een nieuwe array van lengte 2n toe, en kopieert vervolgens de elementen uit de oude array naar de nieuwe.
Gewaarschuwd dit resultaat is overdreven pessimistisch.De volgende n append operaties zullen veel goedkoper zijn -iedereen zal in constante tijd verlopen omdat de nieuw toegewezen array plaats heeft voor alle nieuwe elementen.
Afgeschreven tijd
Een analyse van de afgeschreven tijd geeft een veel beter begrip van het algoritme.
Bekijk een reeks van n append operaties, waarbij we beginnen met een array van lengte 1. Een zorgvuldige analyse laat zien dat de totale tijd van deze operaties slechts Θ(n) is.
- Er zullen in totaal n constante-tijd operaties van toewijzing en toename zijn.
- De herschaling zal alleen gebeuren bij operatie 1, 2, 4, …, 2k, voor een totaal van 1 + 2 + 4 + …+ 2k = 2-2k – 1 constante-tijd operaties van elementkopie. Aangezien 2k ≤ n, is dit maximaal 2n – 1.
Hieruit volgt dat de geamortiseerde tijdcomplexiteit voor een enkele append operatie Θ(1) is.
Meer over algoritme-analyse

Tijdcomplexiteit: Tel je stappen

Grote O-notatie